今回はAi分布についてわかりやすく解説していきたいと思います。
Ai分布は建築の構造設計の地震荷重の算定に必要な要素です。ぜひこの記事を参考にしてみて下さい!!

Ai分布ってなんだ??
Ai分布とは

Ai分布とは層せん断力係数の高さ方向の分布を表したもので、1階の分布係数を1.0とし上の階になればなるほど分布係数は大きくなります。
また1次固有周期が長くなればなるほど大きな値となります。
Ai分布の記号は[Ai]で表し、単位は無次元です。Ai分布を式で表すと
[Ai分布]
\(A_{i}=1+\left(\dfrac{1}{\sqrt{\alpha_{i}}}-\alpha_{i}\right)\dfrac{2T}{1+3T}\)
\(\displaystyle\alpha_{i}=\sum_{j=i}^{n}W_{j} /\sum_{j=1}^{n}W_{j}\)
\(\displaystyle\sum_{j=i}^{n}W_{j}\):当該階より上階の重量の総和
\(\displaystyle\sum_{j=1}^{n}W_{j}\):1階より上階の重量の総和
T:1次固有周期
1次固有周期とは
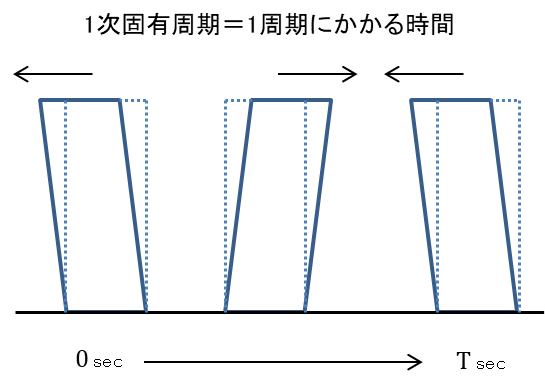
1次固有周期とは建築物が揺れる際の建物の周期(振幅の1往復)にかかる時間を指します。概算法による1次固有周期は建物高さから求めることができますが。精算方による固有周期は手計算では求めることが困難なので解析ソフトから求めます。
1次固有周期は記号は[T]で表し、単位は時間-秒の[sec]や[s]です。算定式は
[1次固有周期-概算法]
\(T=h(0.02+0.01\alpha)\)
h:当該建築物の高さ
α:当該建築物のうち柱及びはりの大部分が鉄骨造である階(地階を除く)の高さの合計のhに対する比(鉄骨造の場合 α=1)
αは当該建築物が鉄骨造であればα=1.0、鉄筋コンクリート造であればα=0になります。式で表すと
α=(鉄骨造部分の階高)/(当該建築物の高さ)
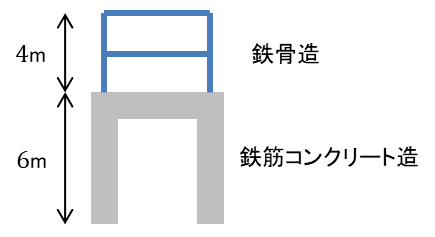
例えば鉄骨造部分の階高が4mで建物高さが10mとした場合の1次固有周期は
\(\alpha=4/10=0.4\)
\(T=10(0.02+0.01\cdot 0.4)=0.24\)
Ai分布の計算例
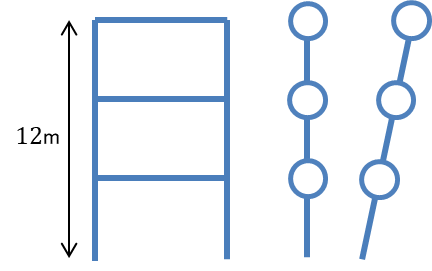
ここでAi分布の具体的な計算例を示します。
- 4階建ての建物
- 各階の床荷重は100m2
- 固定荷重はコンクリートスラブt=150mm (仕上無し)のみで壁は考慮しない
- コンクリートの単位体積重量は24kN/m3
- 積載荷重は1,2,3Fは事務室、4階は屋上広場
- 建築物の高さH=12m
- 主構造は鉄骨造
1.各階の重量を求める
まずは2,3,4階の固定荷重と積載荷重を求めます。この際の1階の重量は考慮しません。
固定荷重はコンクリートスラブの重量のみなので各階の固定荷重は
\(DL=0.15\cdot 100 \cdot 24 =360kN\)
積載荷重は事務室の表の(は)の地震用積載荷重を使います。
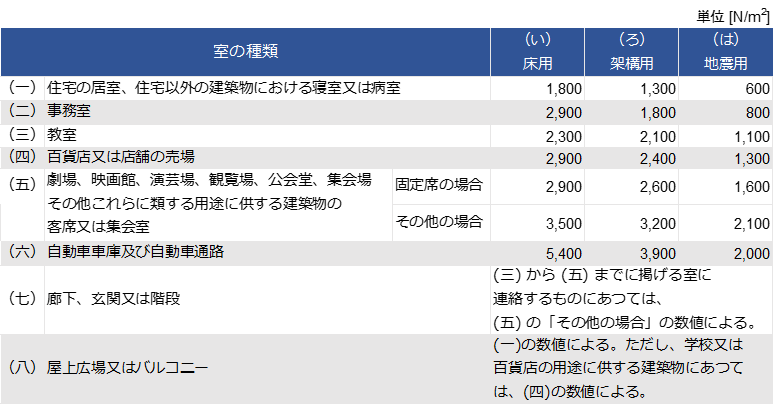
2,3階の積載荷重は
\(LL=0.8\cdot 100=80kN\)
4階の積載荷重は
\(LL=0.6\cdot 100=60kN\)
まとめると
| 階 | 固定荷重 | 積載荷重 | 合計 |
|---|---|---|---|
| 4F(3層) | 360kN | 60kN | 420kN |
| 3F(2層) | 360kN | 80kN | 440kN |
| 2F(1層) | 360kN | 80kN | 440kN |
2. 1次固有周期を求める
1次固有周期は建築物の主構造と建物高さがわかれば求めることができます。
\(\alpha=1.0\)
\(T=12(0.02+0.01\cdot 1.0)=0.36\)
3.αiを求める
つぎにαiを各階の重量から求めます。αiは以下の式で表します。
\(\displaystyle\alpha_{i}=\sum_{j=i}^{n}W_{j} /\sum_{j=1}^{n}W_{j}\)
\(\displaystyle\sum_{j=i}^{n}W_{j}\):当該階より上階の重量の総和
\(\displaystyle\sum_{j=1}^{n}W_{j}\):1階より上階の重量の総和
ただしこの式ではΣがあり、わかりづらいので言葉で言い表すと
αi =(当該階よりも上階の重量の総和)/(全層の重量の総和)
先ほどの表を用い、αiを計算します。
| 階 | 固定荷重 | 積載荷重 | 固定+積載 | 当該階よりも 上階の重量の総和 | αi |
|---|---|---|---|---|---|
| 4F(3層) | 360kN | 60kN | 420kN | 420kN | 0.323 |
| 3F(2層) | 360kN | 80kN | 440kN | 860kN | 0.662 |
| 2F(1層) | 360kN | 80kN | 440kN | 1300kN | 1.000 |
| 全層の合計 | – | – | 1300kN | – | – |
4.Ai分布を求める
最後に1次固有周期とαiからAi分布を求めます。
[Ai分布]
\(A_{i}=1+\left(\dfrac{1}{\sqrt{\alpha_{i}}}-\alpha_{i}\right)\dfrac{2T}{1+3T}\)
T:1次固有周期
\(\dfrac{2T}{1+3T}=\dfrac{2\cdot 0.36}{1+3\cdot 0.36}=\dfrac{9}{26}\)
計算すると
| 階 | 固定+積載 | 当該階よりも 上階の重量の総和 | αi | Ai |
|---|---|---|---|---|
| 4F(3層) | 420kN | 420kN | 0.323 | 1.497 |
| 3F(2層) | 440kN | 860kN | 0.662 | 1.196 |
| 2F(1層) | 440kN | 1300kN | 1.000 | 1.000 |
| 全層の合計 | 1300kN | – | – | – |
このようにAi分布を求めることができました。
引用元:建築物荷重指針・同解説
まとめ
今回はAi分布についてまとめてきました。Ai分布はとても複雑です。求めるものが多く、難しいのでもしも忘れてしまった場合はこの記事を参考にしてみてください!!
- \(A_{i}=1+\left(\dfrac{1}{\sqrt{\alpha_{i}}}-\alpha_{i}\right)\dfrac{2T}{1+3T}\)
- αi =(当該階よりも上階の重量の総和)/(全層の重量の総和)


コメント