今回は曲げモーメントの補正係数についてわかりやすく解説していきたいと思います。
曲げモーメントの補正係数は許容曲げ応力度を使う際に必要な知識です。ぜひこの記事を参考にしてみて下さい!!

曲げモーメントの補正係数ってなんだ??
曲げモーメントの補正係数Cとは

曲げモーメントの補正係数は許容曲げ応力度の算出する際に使う値のうちのひとつで、
曲げモーメントが材長に沿って変化する場合、部材の横座屈による耐力が増減するので、補正係数を設定することで、許容曲げ応力度を調整できるようになっています。
曲げモーメントの補正係数の他にも呼び方が複数存在し、「曲げモーメント係数」、「横座屈モーメント係数」、「弾性横座屈モーメントの補正係数」などがありますが基本的な考え方はすべて同じだと考えます。
記号はほとんどの場合で[C]で表し、他にも[Cb]で表されることもあります。
曲げモーメントの補正係数の計算式
曲げモーメントの補正係数の計算式は2つのパターンがあります。
鋼構造許容応力度設計規準-1970年度版と2005年版では計算式が異なります。(+1.05か-1.05の正負記号は変わり)基本的な式の構成の自体は変わりありませんが補足文章で正負が逆転しています。
どちらも間違いではないのでたどり着く結果は必ず同じになります。
1970年度版
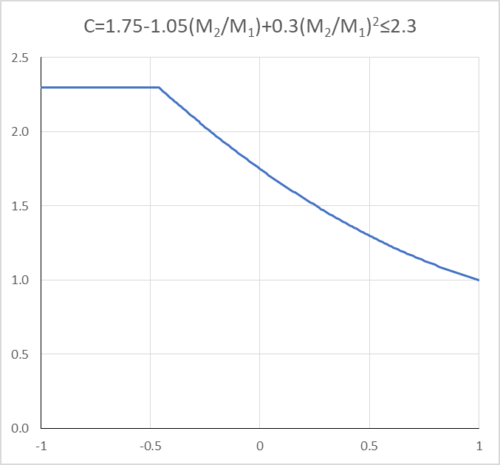

$$C=1.75-1.05\left(\dfrac{M_{2}}{M_{1}}\right)+0.3\left(\dfrac{M_{2}}{M_{1}}\right)^2$$
ただし2.3以下
M1,M2:それぞれ座屈区間端部において小さいほうおよび大きいほうの強軸周りの曲げモーメント(M2/M1)は単曲率の場合は正、複曲率の場合は負とする。区間中間モーメントがM1より大きい場合にはC=1.0とする。
2005年度版
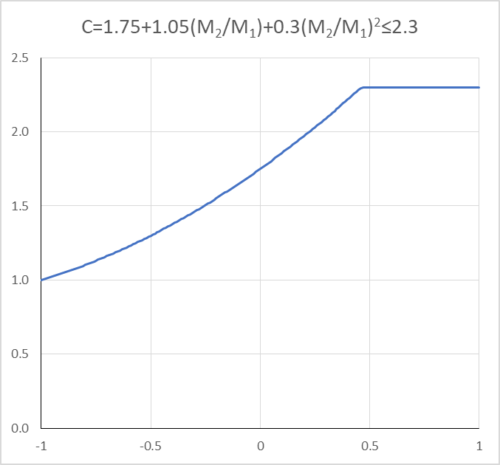

\(C=1.75+1.05\left(\dfrac{M_{2}}{M_{1}}\right)+0.3\left(\dfrac{M_{2}}{M_{1}}\right)^2\)
ただし2.3以下
M1,M2:それぞれ座屈区間端部において小さいほうおよび大きいほうの強軸周りの曲げモーメント(M2/M1)は単曲率の場合は負、複曲率の場合は正とする。区間中間モーメントがM1より大きい場合にはC=1.0とする。
近年の参考図書は2005年の式を使われていることが多いです。
M1とM2とは
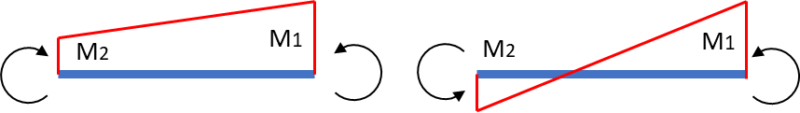
M1とは座屈区間端部の大きいほうの強軸周りの曲げモーメントをM1、
M2とは座屈区間端部の小さいほうの強軸周りの曲げモーメントをM2 と定義されています。式で表すと
\(-1.0 \leq \dfrac{M_{2}}{M_{1}} \leq 1.0\)
単曲率とは

単曲率とは曲率が一つ、つまりはM1とM2の正負符号が異符号の状態を指します。式で表すと
\(-1.0 \leq \dfrac{M_{2}}{M_{1}} \leq 0\)

ここで注意すべきなのが上図のような状態です。梁は複曲率のように曲げモーメントを受けていますが注目するのは端部のM1とM2だけになると異符号になるので単曲率となります。
複曲率とは
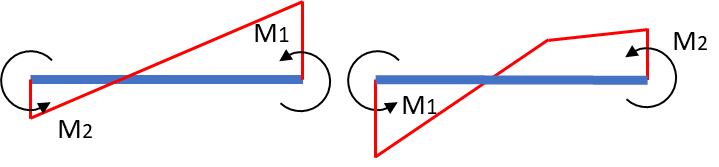
複曲率とは単曲率の逆で曲率が二つ、つまりはM1とM2の正負符号が同符号の状態を指します。式で表すと
\(0 \leq \dfrac{M_{2}}{M_{1}} \leq 1.0\)
区間中間モーメントがM1より大きい場合とは

区間内中間モーメントがM1より大きい場合とはある曲げモーメントM0がM1よりも大きいとき、つまり|M0|>|M1|が成立する場合を指します。
その場合はCの算出式を無視し、C=1.0になります。
\(C=1.0\)
C=1.0となる時が許容曲げ応力度が最も小さくなる状態なので安全側でC=1.0と決め打ちして設計することもあります。
許容曲げ応力度についても詳しい解説はこちらの記事を参考にしてみて下さい!!
まとめ
今回は曲げモーメントの補正係数についてまとめてみました
曲げモーメントの補正係数は許容曲げ応力度の算出に必要な値の一つです。
構造設計を普段やったことのない方は使うことがなく、見慣れない人の方がほとんどだと思いますが、大学生で勉強している方や構造設計を生業とする場合は頭の片隅程度に覚えてください。
許容曲げ応力度を確認する場合はぜひ本ブログを読み直してみて下さい!!


コメント