今回のは断面二次半径についてまとめていきたいと思います
断面二次半径は細長比や一次設計にあたる許容応力度設計を行うために必要なパラメーターです
また断面二次モーメントとも相関関係がありますので合わせて覚えていただくとよいでしょう
断面二次半径とは
断面二次半径とは部材の細長比を求めるのに必要なパラメータです。
細長比は λ = Lb / i で表され、分母に断面二次半径が来るので
断面二次半径が大きいほど座屈しにくくなり、断面二次半径が小さければ座屈しやすいと判断できます。
単位は[cm]や[mm]で表記されることが多いです。断面二次半径は式で表すと
\(i=\sqrt{\dfrac{I}{A}}\)
\(i\) :断面二次半径
\(I\) :断面二次モーメント
\(A\) :断面積
一般的には i の後ろにx,yをつけ、X軸,Y軸周りの断面二次半径ix、iyと表します。
また一般的に断面二次半径の値は文献などに記載があるのでチェックしてみてください。
強軸と弱軸が分かりづらい場合は断面二次半径を比較することですぐに強軸弱軸を判断することができます。(断面二次半径の大きいほうが強軸、小さいほうが弱軸)
断面二次半径の算出例
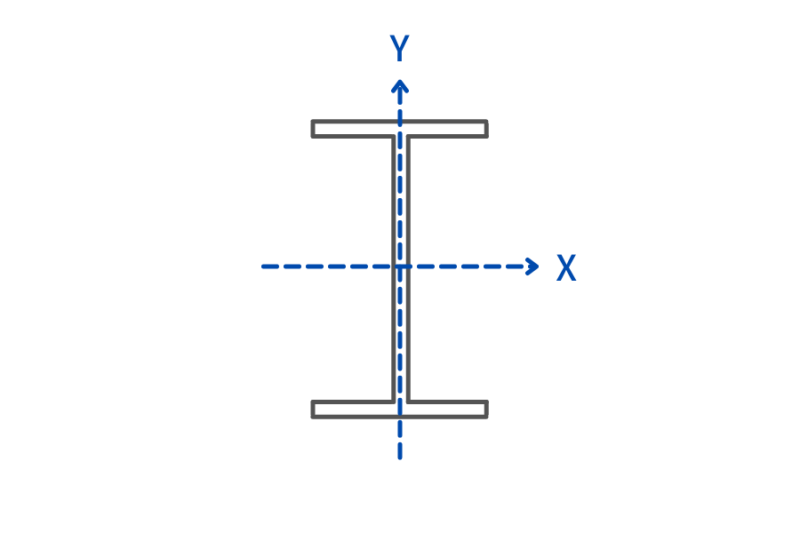
H-100x100x6x8の場合
断面積A=21.5㎝2 断面積二次モーメントIx=378㎝4, Iy=134㎝4
X軸周り(強軸)
ix=√(378/21.5)=4.19cm
Y軸周り(弱軸)
iy=√(134/21.5)=2.49cm
曲げの応力ための断面性能 ib
断面二次半径と似たような値でH型鋼には許容曲げ応力度算定用の断面性能 ib が存在します。
ibは圧縮フランジ梁せいの1/6からなる断面のウェブ軸周りの断面二次半径を指します。
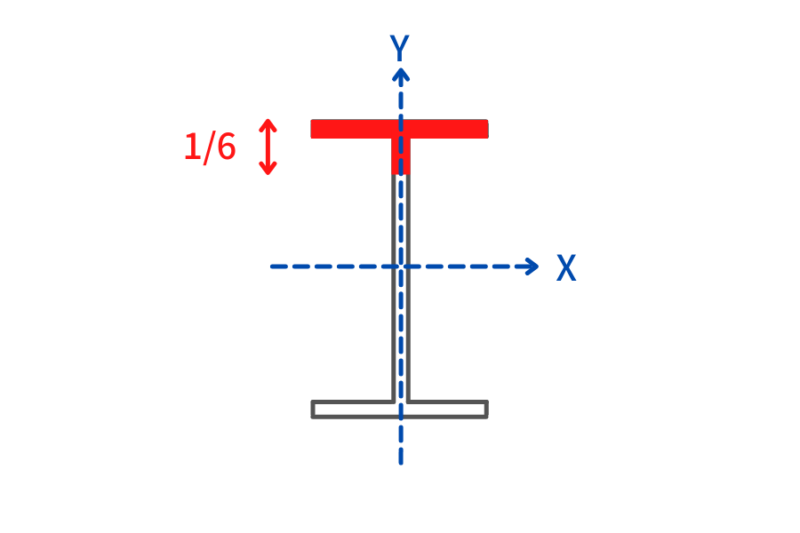
ibの算出例
H-100x100x6x8(フレット部を無視)の場合
せい H=100 ,幅 B=100, フランジ厚 tf=8 , ウェブ厚 tw=6
Af=B*tf=100*8=800㎜2
Aw=(B/6-tf)*tw=52㎜2
A=Af+Aw=852㎜2
I=tf*B3 /12+ (B/6-tf)*tw3/12
I=8*1003 /12 + 8.6…*63/12 =666822.6…㎜4
ib=√(I/A)=√(666822.6…/852)=27.9㎜
文献などにはib=27.5㎜とありますので多少の誤差はありますがほぼ一致しているといえます。
まとめ
今回は断面二次半径についてまとめてきました。
断面二次半径は断面二次モーメントと断面積によって求められます。
また曲げの許容応力度算定に必要なibについても説明しました。
それぞれについてキチンと理解を整理しましょう!!


コメント