断面二次モーメントとは

今回の記事では断面二次モーメントについてわかりやすく説明していきたいと思います

断面二次モーメントは大学生の材料力学で最初に習うこともあり、構造を学ぶ上でも最も重要な項目のひとつでもあります

一級建築士の構造でも頻出の問題です

しっかりと理解できるよう説明していきます

断面二次モーメントとは

断面二次モーメントとは形による変形のしやすさを表すパラメーターです。特徴は値が大きいほど変形しにくく、小さいほど変形しやすくなります。

部材の変形しやすさは主にヤング係数と断面二次モーメントで決まります。

ヤング係数は材料そのものによって決まる値で木材なら木材、鉄なら鉄、コンクリートならコンクリートのヤング係数を使うことになります

断面二次モーメントとヤング係数を掛け合わせ、部材の曲がりにくさを表した値を曲げ剛性と呼びます。

記号は[I]で表すことが多く、x軸周りは[Ix] y軸周りは[Iy]のように表記します。

単位はおもに[cm⁴]や[ｍｍ⁴]で表すことが多いです。

断面二次モーメントを公式で表すと

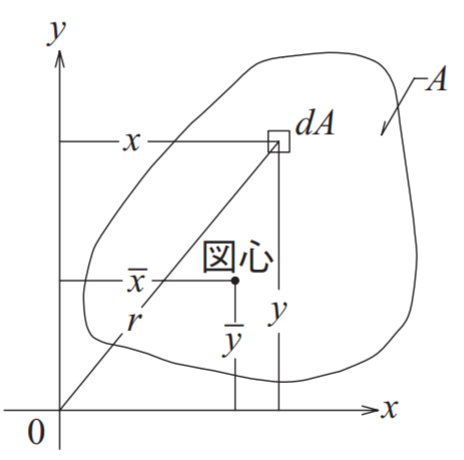
断面二次モーメントはすべて 上記の式から導出できますが

上記の式からだけではなかなか想像できないので

長方形・円形の基本の公式は

軸の平行移動による断面二次モーメントの算出

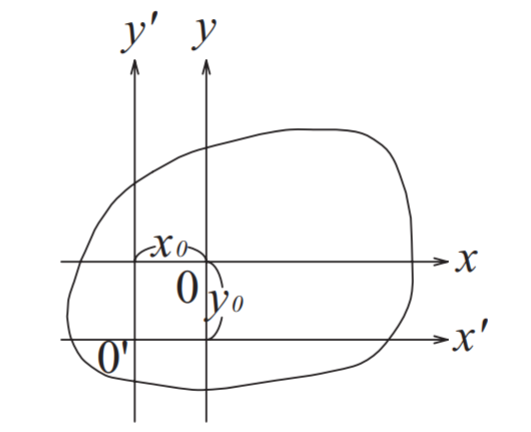
断面二次モーメントの公式と同じくらい重要である軸の平行移動についても覚える必要があります

原点0から軸を0’まで平行移動したときの断面二次モーメントの公式は

長方形の断面二次モーメントの算出

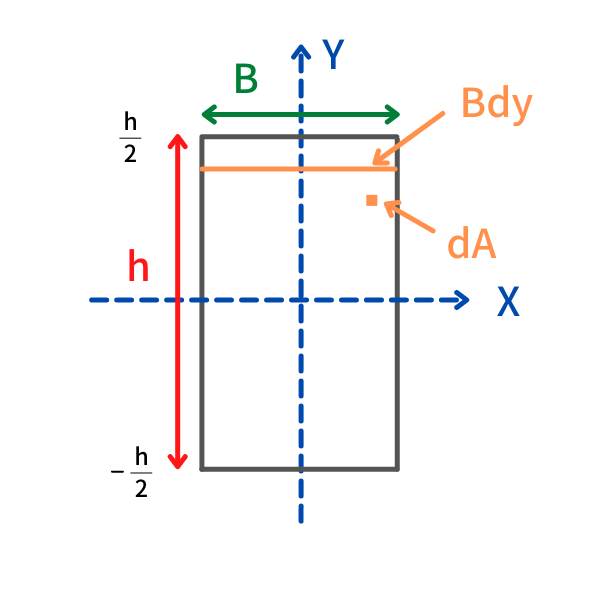
長方形の断面二次モーメントを公式からの算出方法は

まずdAの微小面積要素はB幅に並べると

\(dA=B\times dy\) になります

また積分区間が[-h/2,h/2]になるので公式をこのように変化させます

\( I_{x}=\int y^2dA \) ⇒ \( \displaystyle I_{x} =\int_{-\frac{h}{2}}^{\frac{h}{2}} y^2Bdy \)

X軸周りに対して対象であることからシンプルに表すと

⇒ \( \displaystyle I_{x} =2 \int_{0}^{\frac{h}{2}} y^2Bdy \)

ここからは高校数学の積分で解けるので

\(I_{x}=2B\left[ \dfrac{y^3}{3}\right]_{0}^{\frac{h}{2}}=\dfrac{Bh^3}{12}\)

となり長方形の断面二次モーメントの公式になります

H形鋼の断面二次モーメントの算出法

H型鋼の断面二次モーメントの算出方法は主に2通りあります

• 最外形の断面二次モーメントから断面のない部分の断面二次モーメントを引き算する方法
• フランジ部分とウェブ部分の断面二次モーメントを足し算する方法

例題としてH-100x100x6x8の強軸周りの断面二次モーメントを2種類の方法で計算していきます
(単位はcm、フレット部は無視します)

１．引き算で算出する方法

①最外形の断面二次モーメントの算出

\begin{align}\dfrac{BD^3}{12}=\dfrac{10\times 10^3}{12}=833.3\end{align}

②断面がない部分の断面二次モーメントの算出

\begin{align}\dfrac{bd^3}{12}=\dfrac{(100-2\times8)\times (100-6)^3}{12}=464.3\end{align}

③引き算をする

\begin{align} 833.3-464.3=369.0cm^4\end{align}

２．足し算で算出する方法

①フランジ部の断面二次モーメントの算出

\begin{align}I_{x}=\dfrac{Bt_{f}^3}{12}=\dfrac{10\times 0.8^3}{12}=0.426\end{align}

\begin{align}A_{f}=B\times t_{f} = 10\times 0.8 = 8\end{align}
\begin{align}y_{0}=\dfrac{H}{2}-\dfrac{t_{f}}{2}=4.6\end{align}

\begin{align}I_{f}=2(I_{x}+A_{f}y_{0}^2) = 2(0.426 + 8\times 4.6^2) = 339.4cm^4\end{align}

②ウェブ部分の断面二次モーメントの算出

\begin{align}I_{w}=\dfrac{t_{w}(H-2t_{f})^2}{12}=\dfrac{0.6(10-2\times 8)^3}{12} = 29.6cm^4\end{align}

③フランジ部とウェブ部の断面二次モーメントを足す

\begin{align}I=I_{f} + I_{w}=339.4+29.6=369.0cm^4\end{align}

円の断面二次モーメントの算出

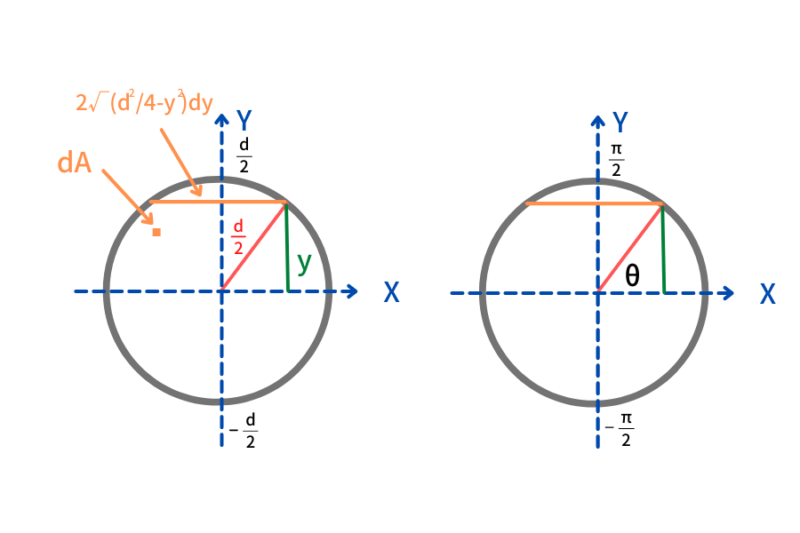
円の断面二次モーメントの算出は

まず長方形と同じく \(dA=B\times dy\) になりますが
Ｂの大きさがX軸からの\(y\)の距離のよって変化するので

\begin{align}dA=2\displaystyle\sqrt{\frac{d^2}{4}-y^2}・dy\end{align}

また積分区間が[-d/2,d/2]になるので

\begin{align}\displaystyle I_{x}=\int y^2dA ⇒ \int_{-\frac{d}{2}}^{\frac{d}{2}} y^2・2\sqrt{\frac{d^2}{4}-y^2}・dy\end{align}

このままでは積分できないので\(y=\frac{d}{2}sin\theta\)とおきます

\begin{align}\displaystyle{\frac{dy}{d\theta}}=\frac{d}{2}cos\theta ⇒ \displaystyle dy=\frac{d}{2}cos\theta d\theta\end{align}

積分区間も\(y ⇒ \theta\)になるので \(-d/2 \le y \le d/2 ⇒ -\pi /2 \le \theta \le \pi /2 \)

\begin{align}\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\frac{d}{2}sin\theta)^2・2\sqrt{\frac{d^2}{4}-(\frac{d}{2}sin\theta)^2}・\frac{d}{2}cos\theta d\theta \end{align}

式変形していき

\begin{align}\displaystyle I_{x} =\frac{d^4}{8}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} sin^2\theta cos^2\theta d\theta\end{align}

倍角の公式\(sin2\theta=2sin\theta cos\theta\)を使い

\begin{align}\displaystyle I_{x} =\frac{d^4}{32}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} sin^2 2\theta d\theta\end{align}

半角の公式\(sin^2 \frac{\theta}{2}=\frac{1-cos\theta}{2}\)を使い

\begin{align}\displaystyle I_{x} =\frac{d^4}{32}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1-cos4\theta}{2}d\theta =\frac{d^4}{32}\left[ \frac{\theta}{2}-\frac{sin4\theta}{8}\right]_{-\frac{\pi}{2}}^\frac{\pi}{2}\end{align}

\begin{align}I_{x} = \displaystyle\frac{\pi d^4}{64} \end{align}

以上で円の断面二次モーメントの算出は終わりです

かなり複雑になりすぎるため覚える必要はないと思います。ご参考までに…

最後に余談ですが楕円の断面二次モーメントは

になります

まとめ

今回は断面二次モーメントについて説明してきました

断面二次モーメントは部材の形による剛性の強さを示す値です。一級建築士試験での頻出問題でもあり、構造の実務でも多用される数値でもあります

長方形の断面二次モーメントの公式は必ず覚えておきましょう！！