今回は構造の弾性座屈荷重についてまとめていきたいと思います
弾性座屈荷重は一級建築士の学科試験の構造でよく出題されます。聞き慣れない言葉も多くあるので難しいと印象を持つ人も少なくありません
この記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
弾性座屈荷重とは
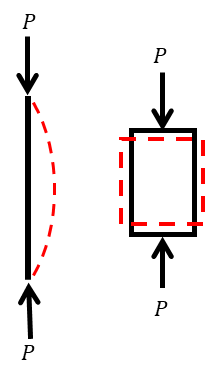
弾性座屈荷重(英:buckling load)とは軸方向に圧縮荷重を受ける一様断面の柱が弾性座屈を起こす荷重を指します。オイラー座屈(英:euler buckling)とも呼ばれます。
弾性座屈は細長い部材に圧縮を加えると部材が横にはらみ出る現象をいいます。逆に部材が太く短い部材であればあるほど弾性座屈は起きにくく、材料強度近くまで強度を発揮できます。
部材の座屈しにくさについてはこちらの記事を参考にしてください→細長比とは
座屈にもたくさんの種類があり
- 弾性座屈(オイラー座屈)
- 非弾性座屈
- 曲げ座屈(横座屈)
- 局部座屈
などがありますが、今回は弾性座屈に焦点をしぼり紹介していきます。
弾性座屈荷重の記号は[Pcr] で表現されます。単位は力の[kN]で表現されます。
式で表すと
[弾性座屈荷重]
\(P_{cr}=\dfrac{\pi^2 EI}{l_{k}^2}\)
E:ヤング係数(弾性係数)
I:断面二次モーメント
lk:座屈長さ
式を見てわかることは、ヤング係数と断面二次モーメントは曲げ剛性を表すパラメーターであり、
ヤング係数は材料による硬さでマシュマロとコンクリートを数値的に表したものと同じで、
断面二次モーメントは断面の形状による硬さで断面積が大きいものと小さいものを数値的に表したもの
座屈長さは長いものと短いものに同じ圧縮力をかけたときにどちらが座屈しやすいかといえば、より長いものの方が座屈することはわかると思います。
これらを掛け合わせたものが剛性です。これらが式で表現されているとわかります。詳しい解説は以下の記事を参考にしてください
座屈荷重公式の導出
梁の微分方程式より
\(\dfrac{d^2y}{dx^2}=-\dfrac{M(x)}{EI}\) …(1)式
\(x\) 離れた距離でのモーメントのつり合いは
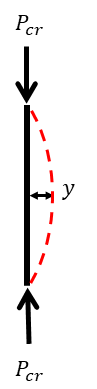
\(Pcr\cdot y=M(x)\) …(2)式
(1)(2)式をまとめると
\(\frac{Pcr}{EI}\cdot y+\frac{d^2y}{dx^2}=0\)
ここで\(k^2=P_{cr}/EI\)とすると
\(k^2\cdot y+\dfrac{d^2y}{dx^2}=0\)
単純梁‐たわみについて\(y(x)=A\cos{kx}+B\sin{kx}+Cx+D\) とおき、
曲げモーメント\(M(x)\)に関してはたわみの2回微分なので\(y^{\prime\prime}(x)\)
\(y^{\prime\prime}(x)=-k^2 A\cos{kx}-k^2 B\sin{kx}\)
\(x=0,l\)で\(y=0\)かつ\(M=0\)になるため
\(y(0)=A\cos{k0}+B\sin{k0}+C\cdot0+D=0\)
\(y(l)=A\cos{kl}+B\sin{kl}+Cl+D=0\)
\(y^{\prime\prime}(0)=-k^2 A\cos{k0}-k^2 B\sin{k0}=0\)
\(y^{\prime\prime}(l)=-k^2 A\cos{kl}-k^2 B\sin{kl}=0\)
これらの式4つを連立すると\(B\sin{kl}=0\)が導かれます。これはつまり
\(B=0\)あるいは\(\sin{kl}=0\)になり\(B=0\)はたわみがない時を意味するので
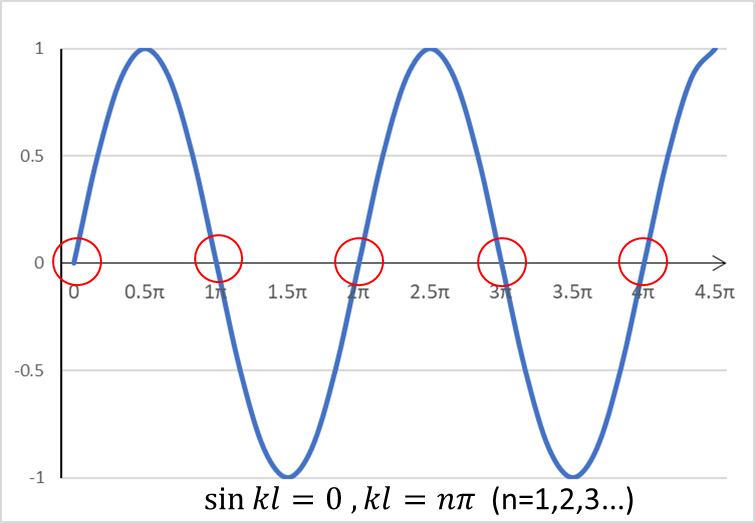
\(\sin{kl}=0\)は\(kl=n\pi\quad(n=0,1,2,3…)\)になるときに成り立ちます
\(k=\dfrac{n\pi}{l} \quad(n=0,1,2,3…)\)…(3)式
\(k^2=P_{cr}/EI\)の式に戻り(3)式を適用すると
\(P_{cr}=n^2 \dfrac{\pi^2 EI}{l}\quad(n=0,1,2,3…)\)
n=0はたわみなし、n=1はたわみの1次モード、n=2はたわみの2次モード…のように考えて下さい
ここまでは長々と説明しましたが一級建築士には導出方法は必要ありませんので公式だけ覚えて帰ってください!!
座屈荷重の求め方
座屈荷重の求め方は
- 柱(圧縮材)の座屈長さを求める
- 断面二次モーメントとヤング係数を求める
- 座屈荷重を求める
ラーメン架構の柱の座屈荷重
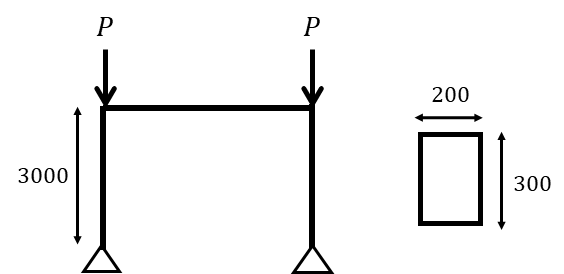
具体的なラーメン架構をみながら解いていきます。ラーメン架構の梁は剛接合とし柱脚はピンとします。
柱の長さを3000mm 部材断面を200×300とし、ヤング係数は鉄骨を想定し、205000N/mm2 柱をつなげる梁は十分に剛体であり、面外方向の座屈は考慮しないものとします。
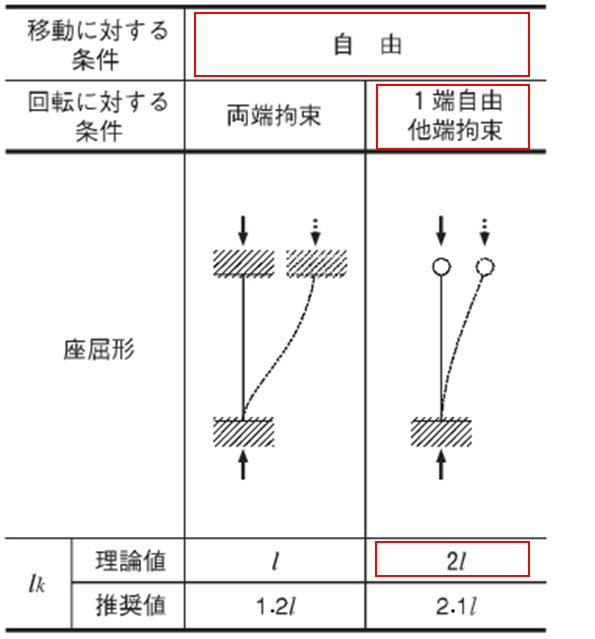
まず柱の座屈係数を算出します。ラーメン架構なので水平移動は自由、回転に対しては自由一端拘束・一端自由となるので
\(l_{k}=2.0l=2\cdot 3000=6000\)
つぎに断面二次モーメントは今回は弱軸ラーメン架構とし、強軸は座屈しないものと仮定するので
\(I=\dfrac{300\cdot 200^3}{12}\)
\(I=2.0\cdot 10^8 mm^4\)
ヤング係数は鉄骨の一般的な値を用います
\(E=205000N/mm^2\)
最後に座屈荷重の公式から
\(P_{cr}=\dfrac{\pi^2 EI}{l_{k}^2}\)
\(P_{cr}=\dfrac{3.14^2 \cdot 2.0\cdot 10^8\cdot 205000}{6000^2}\)
\(=11240kN\)
このように求めることができます
ブレース架構の柱の座屈荷重

次はブレース架構を解いていきます。ブレース架構の梁はピン接合とし柱脚はピンとします
柱の長さを3000mm 部材断面を200×300とし、ヤング係数は鉄骨を想定し、205000N/mm2 柱をつなげる梁は十分に剛体であり、面外方向の座屈は考慮しないものとします。
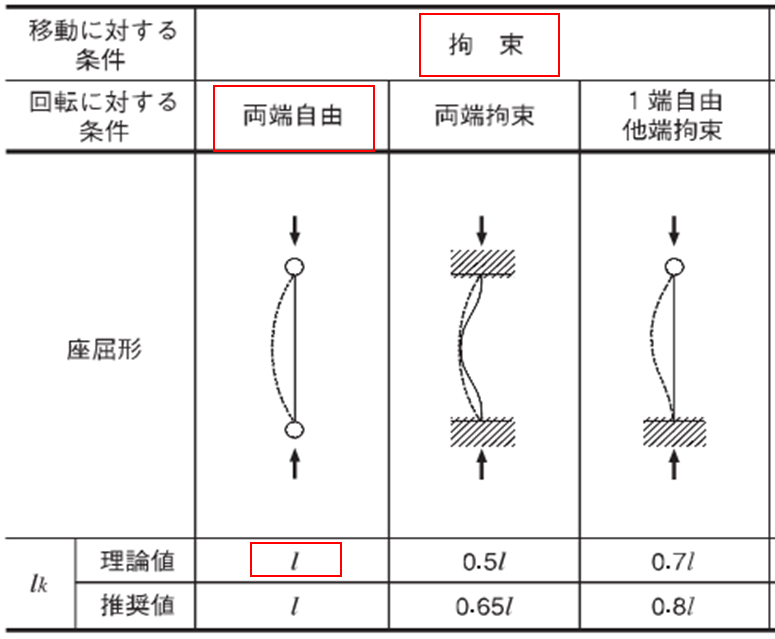
まず柱の座屈係数を算出します。ブレース架構なので水平移動は拘束、回転に対して両端自由となるので
\(l_{k}=1.0l=1\cdot 3000=3000\)
つぎに断面二次モーメントは今回は弱軸ブレース架構とし、強軸は座屈しないものと仮定するので
\(I=\dfrac{300\cdot 200^3}{12}\)
\(I=2.0\cdot 10^8 mm^4\)
ヤング係数は鉄骨の一般的な値を用います
\(E=205000N/mm^2\)
最後に座屈荷重の公式から
\(P_{cr}=\dfrac{\pi^2 EI}{l_{k}^2}\)
\(P_{cr}=\dfrac{3.14^2 \cdot 2.0\cdot 10^8\cdot 205000}{3000^2}\)
\(=44961kN\)
同じ形状の架構であってもブレース架構はラーメン架構の4倍座屈荷重のが増えることがわかりました。
まとめ
今回は弾性座屈荷重についてまとめてみました
弾性座屈荷重は軸方向に圧縮荷重を受ける一様断面の柱が弾性座屈を起こす荷重を指します。
一級建築士試験において弾性座屈荷重の求め方は覚える必要はありませんが、弾性座屈荷重の公式については必ず覚えてください
弾性座屈荷重は難しい分野ではありますが計算自体は難しくないため、ぜひ何度も読み直し理解してみて下さい!!




コメント