今回は2020年度一級建築士 学科試験Ⅳ構造のNo.3の問題についてまとめていきたいと思います。
今回は構造力学の水平剛性の問題から出題されています。
水平剛性の問題を初めて見る人も多いとおもいます。この記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

柱の水平剛性!!どうやって解くの!?
問題 No.3
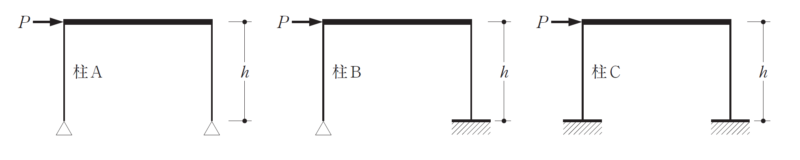
[No.3]
図のような柱脚の支持条件が異なる3 つのラーメンに水平荷重P が作用する場合、柱A、柱B及び柱Cに生じるせん断力をそれぞれQA、QB及びQCとしたとき、それらの大小関係として、正しいものは、次のうちどれか。ただし、全ての柱は等質等断面の弾性部材とし、梁は剛体とする。
[選択肢]
- QA>QB>QC
- QA=QC>QB
- QB>QA=QC
- QC>QB>QA
この問題キーワードは
- 梁の水平剛性の求め方
- 柱の剛比と柱のせん断力の関係
前提条件
この問題は以下の知識について問われています
- 柱の水平剛性
- 柱の剛比
ひとつずつ紐解いていきましょう!!
水平剛性とは
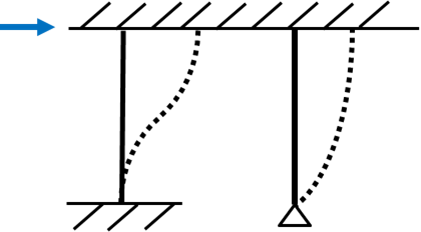
水平剛性(英:horizontal stiffness)とは梁や床をなす架構や層に対してある一定の力が水平方向(横)からかけられると、層は力と同じ向きに水平移動します。
そのときの水平の移動量に対して柱や壁は抵抗しようと逆向きにバネのような抵抗力がはたらきます。このときの水平方向の抵抗力を水平剛性あるいは柱や壁(鉛直部材)による水平方向の硬さとも言えます。
水平剛性は高層ビルなど縦に長い建物を例えるとイメージしやすいです。地震のような水平力を受け横に揺れたとき、水平剛性が大きいがっちりとした建物であれば揺れは小さく、水平剛性が小さいやわらかい建物であれば揺れは大きくなります。
建物や建築で言う水平剛性は耐震性とも言えます
水平剛性の記号は[k]で表されることが多く、単位は[N/mm]や[kN/m]で表されることが多いです。水平剛性を式で表すと
[水平剛性]
\(k=\dfrac{Q}{\delta}\)
Q:水平力(層せん断力)
δ:水平変位
[ピン支点-水平剛性]
\(k=\dfrac{3EI}{L^3}\)
[固定支点-水平剛性]
\(k=\dfrac{12EI}{L^3}\)
E:ヤング係数
I:断面二次モーメント
L:部材長
それぞれの公式の導出についてはこちらの記事を参考にしてみて下さい。
剛比とは
剛比とは部材が持つ剛性の比率です。
キーワードは「剛性が高ければ力は集まる」つまり剛性の高い部材は負担する力も大きくなり、剛性の小さい部材は負担する力も小さくなります。
別の言い方でいうと『力の負担割合』といえます。式で表すと
[剛比]
\(\dfrac{k{i}}{\Sigma k}\)
ki:剛比を求めたい部材の剛性
Σk:部材の剛性の合計
解き方

解く順序は
- 支点条件による水平剛性の式をたてる
- 柱の剛比(水平剛性をたてる)
- 柱のせん断力を求める
ひとつずつ算出していきましょう
まずは支点条件による水平剛性の式をたてると公式よりピン支点は
\(k=\dfrac{3EI}{h^3}\)
固定支点では
\(k=\dfrac{12EI}{h^3}\)
それぞれ柱に剛性を書き込むと

つぎに剛比を求めます。剛比は(求めたい部材の剛性)/(部材の剛性の合計)で表せるので
柱Aの剛比
\(\dfrac{3EI}{h^3}/(2\cdot \dfrac{3EI}{h^3})=0.5\)
柱Bの剛比
\(\dfrac{3EI}{h^3}/(\dfrac{3EI}{h^3}+\dfrac{12EI}{h^3})=0.2\)
柱Cの剛比
\(\dfrac{12EI}{h^3}/(2\cdot \dfrac{12EI}{h^3})=0.5\)
最後に柱のせん断力をもとめます。水平剛性の比(左右の柱の剛性比)によって負担するせん断力が決まるので
柱Aと柱Cの負担するせん断力は先ほど求めた剛比から
\(Q_{A}=Q_{C}=0.5P\)
柱Bは先ほど求めた剛比から
\(Q_{B}=0.2P\)
答えは『QB<QA=QC』となり、最終的な答えは②でした
まとめ
今回は2020年 一級建築士 学科試験Ⅳ構造 No.3の解説をしてきました
今回のポイントは剛比と水平剛性の関係性を知っていたかどうかです。
水平剛性の公式をすぐに忘れてしまう人も多いかと思いますが、係数がわからなくとも固定支点の剛性は堅く、ピン支点の剛性は柔らかいイメージがあるだけでも問題は解けます。ここだけでも覚えておいてください!!
過去の水平剛性の記事ではたわみの公式から水平剛性を導出できる方法を紹介していますので、是非水平剛性の記事もあわせて是非参考にしてみて下さい!!



コメント