今回は両端固定梁の等分布荷重の曲げモーメントM図・せん断力Q図についてわかりやすく解説していきたいと思います
建築士試験の曲げモーメント・せん断力の問題は基本中の基本であり、もし係数の暗記をしている人はぜひ導出過程も覚えてください。忘れてしまった場合でも試験で点が取れると思います。
ただし固定端の梁は不静定架構に該当するため単純な力のつり合いからでは解くことができませんのでわかりやすく解説していきたいと思います!

両端固定梁の等分布荷重のM図・Q図??
両端固定梁・等分布荷重の曲げモーメント・せん断力
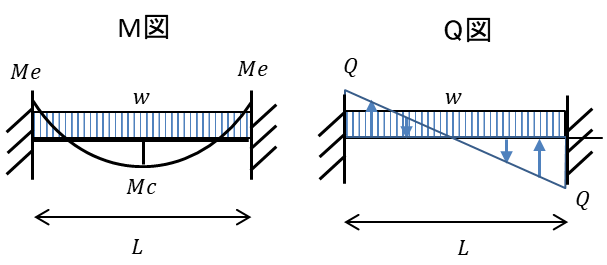
両端固定梁・等分布荷重の曲げモーメントM・せん断力Qを式で表すと
[両端固定梁・等分布荷重の中央曲げモーメント]
\(M_{C}=\dfrac{wL^2}{24}\)
[両端固定梁・等分布荷重の端部曲げモーメント]
\(M_{E}=\dfrac{wL^2}{12}\) (※中央曲げモーメントと向きは逆)
[両端固定梁・等分布荷重のせん断力]
\(Q=\dfrac{wL}{2}\)
w:等分布荷重
L:梁の長さ
両端固定梁・集中荷重の曲げモーメントM・せん断力Qはこちら
両端固定梁-集中荷重のM図・Q図
両端固定梁・等分布荷重の曲げモーメント図
両端固定梁・等分布荷重の曲げモーメント図を描く方法は
- 反力を求める
- \(M(x)\) の式を求める
- たわみ曲線の方程式\(\frac{d^2y}{dx^2}=-\frac{M}{EI}\)を使う
- 引張側にモーメント\(M(x)\) のグラフを描く
まずは反力を求めます。鉛直反力をR1とし、モーメント反力をM1としたとき両端固定梁・等分布荷重の反力は
\(R_{1}=\dfrac{wL}{2}\)
反力から\(x\)進んだところでの\(M(x)\) の式は
\(M(x)=M_{1}-R_{1}x+wx^2=M_{1}-\dfrac{wLx}{2}+\dfrac{wx^2}{2}\) …(1)式

つぎにたわみ曲線の方程式\(\frac{d^2y}{dx^2}=-\frac{M}{EI}\)を使います。
たわみ曲線の方程式のMに先ほどのM(x)を代入すると
\(\dfrac{d^2y}{dx^2}=-\dfrac{M_{1}-\frac{wLx}{2}+\frac{wx^2}{2}}{EI}\)
たわみの曲線方程式を1回積分するとたわみ角、2回積分するとたわみになるので以下のように表せます。
\(\displaystyle \theta(x)=\frac{dy}{dx}=-\int(\frac{M_{1}-\frac{wLx}{2}+\frac{wx^2}{2}}{EI})dx\) …(2)式
\(\displaystyle \delta(x)=y=-\iint(\frac{M_{1}-\frac{wLx}{2}+\frac{wx^2}{2}}{EI})dxdx\) …(3)式
(2)式のたわみ角の積分を解くと
\(\theta(x)=-\dfrac{wx^3}{6EI}+\dfrac{wLx^2}{4EI}-\dfrac{M_{1}x}{EI}+c_{1}\)
このとき積分定数c1を忘れないようにしましょう
境界条件より端部\(x=0\)ではたわみ角が\(\theta=0\)となるので
\(c_{1}=0\) となり
\(\theta(x)=-\dfrac{wx^3}{6EI}+\dfrac{wLx^2}{4EI}-\dfrac{M_{1}x}{EI}\)
同じく境界条件より\(x=L/2\)でも\(\theta=0\)となるのでモーメント反力\(M_{1}\)についても求めることができ
\(\theta(\frac{L}{2})=-\dfrac{w(\frac{L}{2})^3}{6EI}+\dfrac{wL(\frac{L}{2})^2}{4EI}-\dfrac{M_{1}(\frac{L}{2})}{EI}=0\)
上記の式を解くと、支点の曲げモーメント反力は
\(M_{1}=\dfrac{wL^2}{12}\)
中央の曲げモーメントは
\(M(\frac{L}{2})=\dfrac{wL^2}{12}-\dfrac{wL(\frac{L}{2})}{2}+\dfrac{w(\frac{L}{2})^2}{2}=-\dfrac{wL^2}{24}\)
曲げモーメントの式は
\(M(x)=\dfrac{wL^2}{12}-\dfrac{wLx}{2}+\dfrac{wx^2}{2}\)
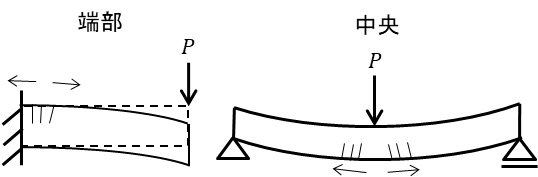
M図は引張側にモーメントを描くので、引張側を調べる必要があります。
両端固定梁に対して下向きの力をかけたときに引張が生じるのは部材の中央で下側、部材の端部で上側に発生するのがイメージできますでしょうか、\(M(x)\) の式が\(x\)の2次関数であることがわかるので、端部で\(M=wL^2/12\) 梁の中央で\(M=-wL^2/24\)となる\(M(x)\)の弧のグラフを描くと
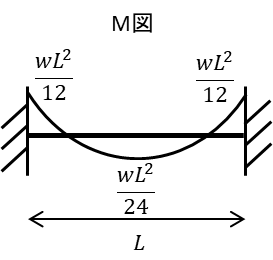
両端固定梁・等分布荷重のせん断力図
両端固定梁・等分布荷重のせん断力図を描く方法は
- 反力を求める
- \(Q(x)\) の式を求める
- \(Q(x)\) のグラフを描く(時計回りは部材の上側、反時計回りを部材の下側)
鉛直反力をR1したとき両端固定梁・等分布荷重の反力は
\(R_{1}=\dfrac{wL}{2}\)
反力から\(x\)進んだところでの\(Q(x)\) の式は
\(Q(x)=R_{1}-wx=\dfrac{wL}{2}-wx\)
Q図は時計回りは部材の上側に、反時計回りは部材の下側に描き、また\(Q(x)\) の式が\(x\)の1次関数であることがわかったので、端部で\(Q=wL/2\) 梁の中央で\(Q=0\)となる\(Q(x)\)の直線のグラフを描くと
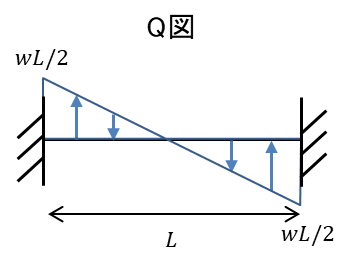
具体的な計算例
最後に両端固定梁ー等分布荷重のM図Q図の具体的な計算を見ていきます
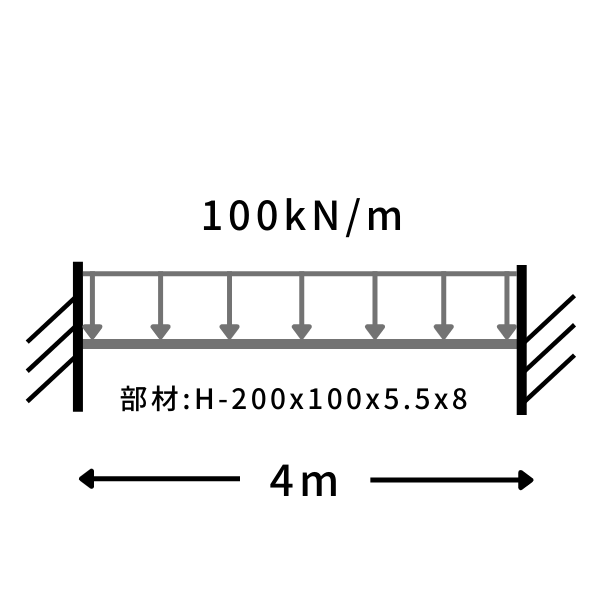
[設計条件]
部材:H-200x100x5.5×8
長さ:L=4m
等分布荷重:100kN/m
[計算過程]
支点の反力は
\(R_{1}=\dfrac{100\cdot 4}{2}=200kN\)
反力から\(x\)進んだところでの\(M(x)\) の式は公式より
\(M(x)=w(\dfrac{L^2}{12}-\dfrac{Lx}{2}+\dfrac{x^2}{2})\)
\(=100(\frac{4^2}{12}-\frac{4x}{2}+\frac{x^2}{2})\)
中央のモーメントは
\(M(2)=-\dfrac{100\cdot 4^2}{24}=-66.66…kN・m\)
端部のモーメントは
\(M(0)=\dfrac{100\cdot 4^2}{12}=133.33…kN・m\)
\(Q(x)\) の式は
\(Q(x)=-100x+200\)
\(Q(2)=0kN\)
したがってM図Q図を描くと
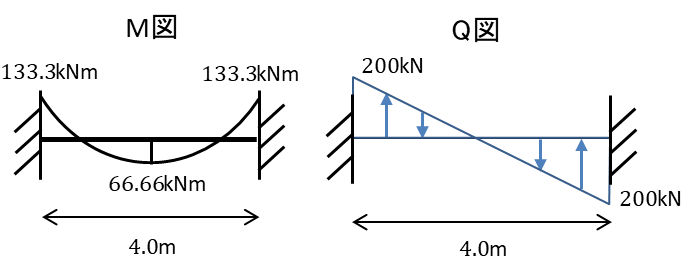
まとめ
今回は両端固定梁・等分布荷重のM図Q図についてまとめてきました。力学の基本のキです。ただし積分が苦手も人もいるため覚えなくてもいいです。公式を覚えるのが苦手な人は導出過程を知っておくとテストでも確実に解くことができます。公式を暗記する必要はありません!!
しっかりこの記事を何度も見て勉強して習得してください!!



コメント