座屈長さとは

今回は座屈長さについてまとめていきたいと思います

座屈長さは細長比・許容圧縮応力度などに必要なパラメーターです

座屈長さについては教科書等でも必ず記載されていますが非常に分かりにくい部分でもあります

この記事ではできる限りわかりやすく説明したいと思います！

座屈長さとは、ある支持条件に対して座屈する部分の長さです

座屈長さの記号は \(Lk\)で表現され、単位は長さの[mm]や[m]です。式で表すと

[座屈長さ]

\(L_{k}= K × L\)

K :座屈長さ係数
L :支点間距離

座屈長さと言っても、一つの部材に対し座屈する方向はX軸、Y軸（強軸・弱軸）の2方向であるため座屈長さをそれぞれ[Lx・Ly] と表現することが多いです

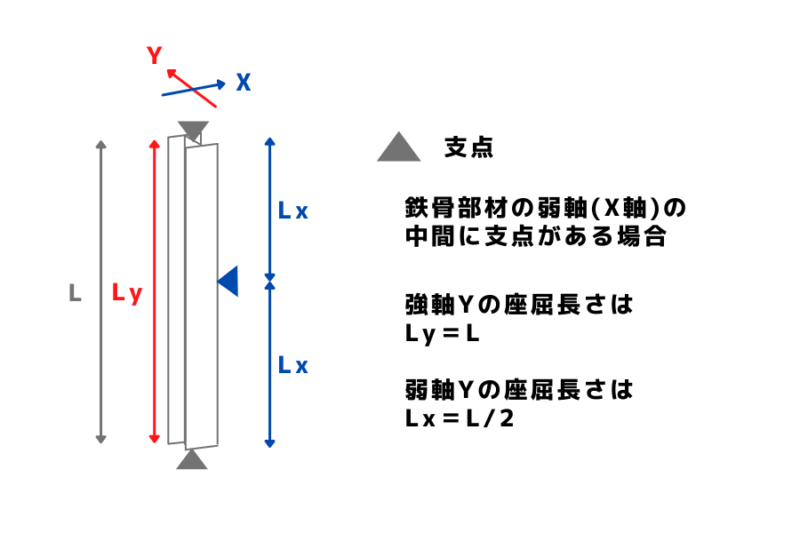
この時の鉄骨部材の細長比は

[細長比]

\(λ_{x}= \dfrac{L_{x}}{i_{x}}\)

\(λ_{y}= \dfrac{L_{y}}{i_{y}}\)

Lx：X軸の座屈長さ
Ly：Y軸の座屈長さ
ix：X軸の断面二次半径
iy：Y軸の断面二次半径

また許容圧縮応力度の算定で用いる細長比は上記のλx、 λyの大きい（座屈しやすい）部材軸の細長比λを用います

座屈長さ係数とは

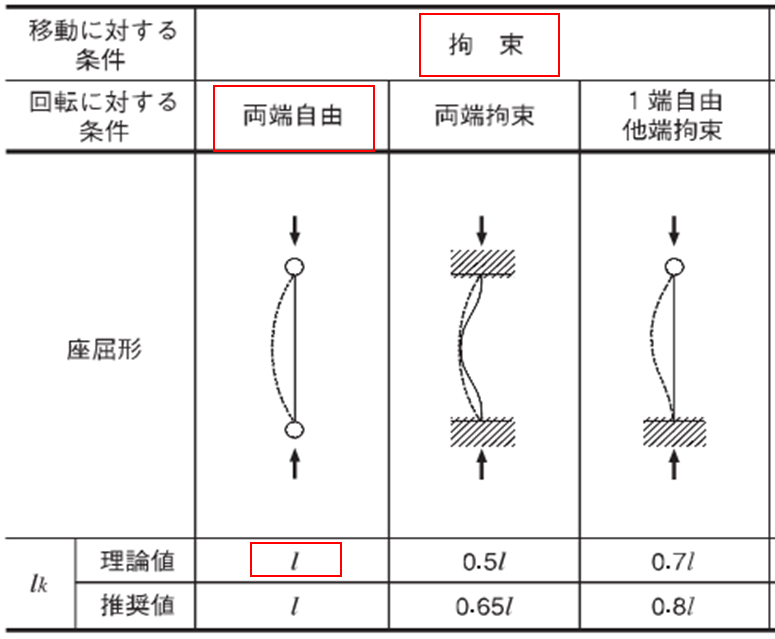
座屈長さ係数は支持条件、境界条件によって値が変わります

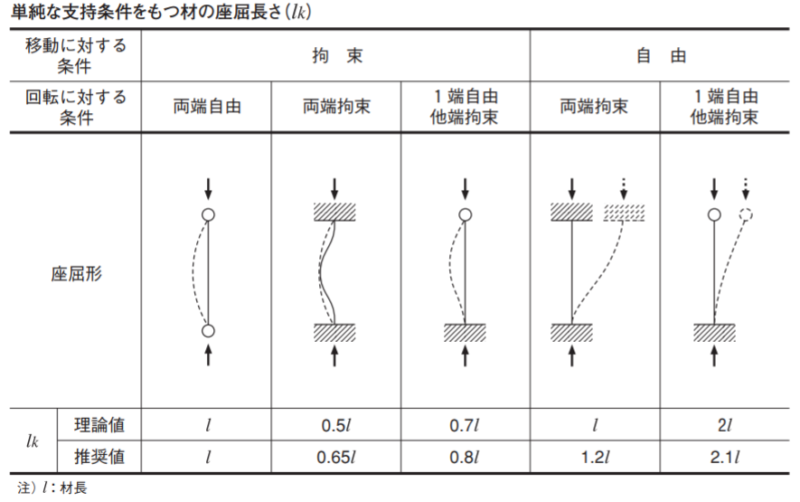
・移動に対する条件【拘束】
　両端自由　K=1.0
　両端拘束　K=0.5
　一端自由　K=0.7

・移動に対する条件【自由】
　両端拘束　K=1.0
　一端拘束　K=2.0 　

移動に対する条件とは

ラーメン架構の柱は水平拘束なし→自由
ブレース架構の柱は水平拘束あり→拘束

回転に対する条件とは

柱端部の条件が剛接合であれば　→拘束
柱端部の条件がピン接合であれば→自由

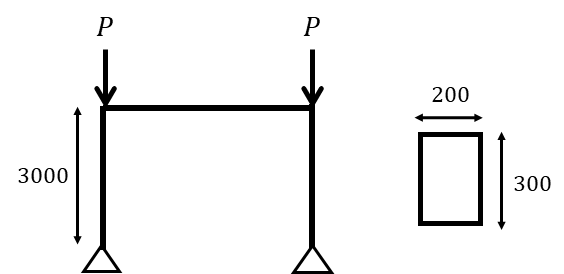
具体的なラーメン架構をみながら解いていきます。ラーメン架構の梁は剛接合とし柱脚はピンとします。

柱の長さを3000mm 部材断面を200×300とし、柱をつなげる梁は十分に剛体であり、面外方向の座屈は考慮しないものとします。

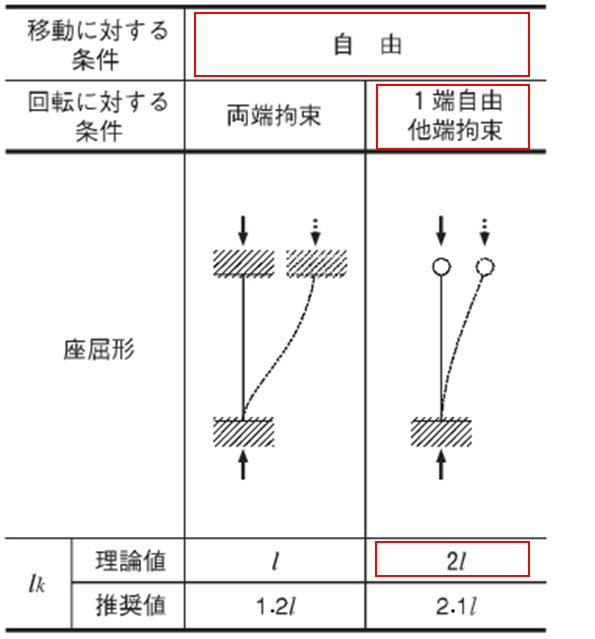
ラーメン架構の柱の座屈係数は水平移動は自由、回転に対しては自由一端拘束・一端自由となるので

\(l_{k}=2.0l=2\cdot 3000=6000\)

次はブレース架構を解いていきます。ブレース架構の梁はピン接合とし柱脚はピンとします

柱の長さを3000mm 部材断面を200×300とし、柱をつなげる梁は十分に剛体であり、面外方向の座屈は考慮しないものとします。

ブレース架構の柱の座屈係数は水平移動は拘束、回転に対して両端自由となるので

\(l_{k}=1.0l=1\cdot 3000=3000\)

座屈長さ係数は特に柱に対して論じられることが多いですが梁に対しても同じことが言えます。基本的に梁は軸力を負担しないという考えのもとで梁の座屈長さ係数を考慮しない場合もありますが、

トラス弦梁や軸力を大きく負担するの梁は座屈長さ係数を正しく把握しないと座屈を起こす可能性があるのでしっかりと確認しましょう！

今回は座屈長さについてまとめてきました。

座屈長さ

水平拘束のない片持ち柱は座屈長さが2.0に大きく変わり座屈しやすくなるので注意が必要です！

座屈長さは座屈しやすさに大きく関わるパラメータです正しく設定できることが一級建築士や構造設計に求められるスキルです！！

座屈長さを忘れてしまったら、この記事を参考にしてみて下さい！！