今回は許容曲げ応力度についてわかりやすく解説していきたいと思います。
許容曲げ応力度は鋼構造を設計する際に使うとても重要な知識です。ぜひこの記事を参考にしてみて下さい！！
許容曲げ応力度ってなんだ？？
許容曲げ応力度fbとは
許容曲げ応力度とは許容応力度設計における許容される応力度つまり、建築基準法で定められた曲げモーメントの応力度です。
許容曲げ応力度は引張応力度とは異なり、横座屈が発生するので単純に基準強度に安全率をかけただけでは算出できないので注意が必要です。
許容応力度設計とは建築基準法施行令第81条2項二のイに規定される設計法で鋼構造においては降伏応力度以下の応力度、
さらに曲げモーメントの場合では横座屈による低減された許容応力度以下の応力度内で部材サイズを選定する方法です。
応力度とは４つに大きく大別されます。
- 引張応力度
- 圧縮応力度
- 曲げ応力度
- せん断応力度
記号は[fb]で表し、bは”bending moment“の頭文字から来ています。単位は[N/mm2]です。
横座屈とは
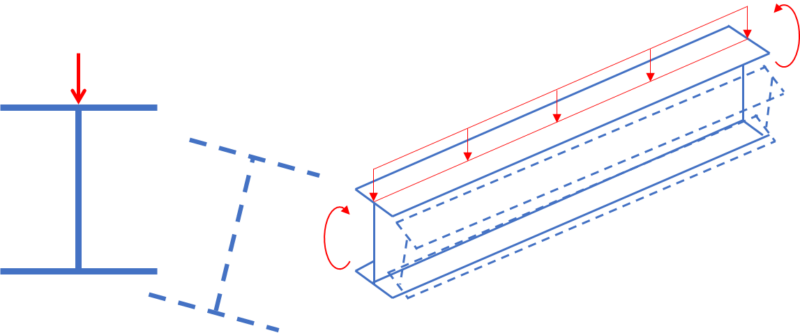
横座屈とは梁の強軸に曲げモーメントを受ける部材が軸対称から逸脱したねじりを伴った変形を弱軸に生じる座屈のことを指します。
横座屈を止める（生じさせない）ためには横補剛材やスチフナーをつけることで対策ができます。
横座屈はイメージしにくい座屈モードのなので見落としがちですが、非常に重要なトピックです。
旧規準(1973年)-許容曲げ応力度
鋼構造設計指針規準の許容曲げ応力度の式は旧規準式と新規準式の２つ存在しています。
旧規準式は建築基準法でも使われていて、手計算で求められるので一般に普及しています。
旧規準式では大きく、a)～e) の５つに分類されます。分類されている意図は鋼材ごとに横座屈の有無や面外・面内などを明確に分ける必要があるからです。
a) 圧延形鋼、プレートガーダー、組立材の許容曲げ応力度
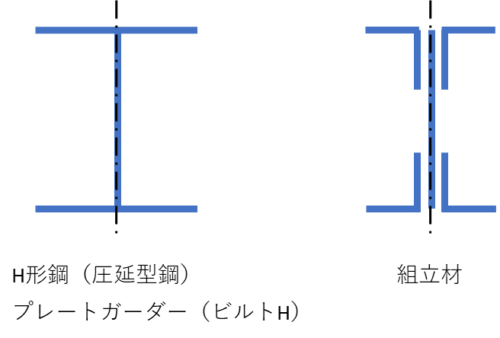
荷重面内に対称軸有する圧延形鋼、プレートガーダー、その他の組立材で幅厚比の制限を満足するものが、強軸周りに曲げを受ける場合（箱型断面を除く）、材の圧縮応力度は、(5.7)、(5.8)式のうち大きいほうをとる。ただし、圧縮応力度、引張応力度ともft(引張許容応力度)を超えることはできない。
[長期-許容曲げ応力度]
\(f_{b}=max[f_{b1},f_{b2}]\)
\(f_{b1}=\left[\dfrac{2}{3}-\dfrac{4}{15C}\left(\dfrac{l_{b}/i_{b}}{\Lambda}\right)^2\right]\cdot F\) …(5.7)式
\(f_{b2}=\dfrac{89000\cdot A_{f}}{l_{b}\cdot h}\leq F/1.5\) …(5.8)式
[短期-許容曲げ応力度] …長期の1.5倍
\(f_{b}=max[f_{b1},f_{b2}]\)
\(f_{b1}=\left[1-\dfrac{0.4}{C}\left(\dfrac{l_{b}/i_{b}}{\Lambda}\right)^2\right]\cdot F\)
\(f_{b2}=\dfrac{89000\cdot A_{f}}{l_{b}\cdot h}\leq F\)
F：基準強度 (N/mm2)
Λ：限界細長比
C：曲げモーメントの補正係数
ib：曲げ応力用の断面２次半径(mm)
lb：梁の横補剛間隔(mm)
Af：圧縮側フランジの断面積(mm2)
h：梁せい(mm)
\(C=1.75-1.05(M_{2}/M_{1})+0.3(M_{2}/M_{1})^2\leq 2.3\)
M1,M2：それぞれ座屈区間端部において小さいほうおよび大きいほうの強軸周りの曲げモーメント(M2/M1)は単曲率の場合は正、複曲率の場合負とする。区間中間モーメントがM1より大きい場合にはC=1.0とする。
Cの曲げモーメントの補正係数についての詳しい解説はこちらの記事を参考にしてみて下さい。
b) 鋼管、箱型断面の許容曲げ応力度
鋼管、箱型断面材および荷重面内に対称軸を有し、かつ弱軸周りに曲げを受ける材で幅厚比の制限に従う場合ならびに面内に曲げを受けるガセットプレートの圧縮および引張側許容曲げ応力度はft(引張許容応力度)とする。
c) みぞ形断面および荷重面内に対称軸を有しない材の許容曲げ応力度
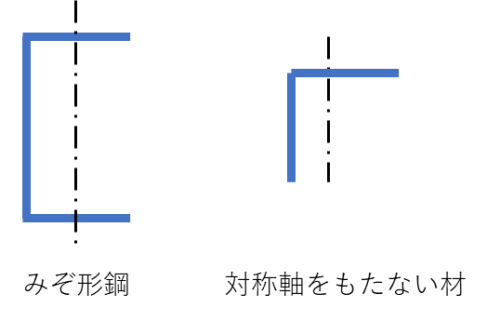
みぞ形断面材および荷重面内に対称軸を有しない材で幅厚比の制限に従う場合、材の圧縮側許容応力度は（5.8）式による。ただし、ft(引張許容応力度)を超えてはならない。
d) ベアリングプレートの許容曲げ応力度
ベアリングプレートなど面外に曲げを受ける板の許容曲げ応力度は（5.9）式の値とする。
\(f_{b1}=F/1.3\) …(5.9)式
F：基準強度 (N/mm2)
e) 曲げを受けるピンの許容曲げ応力度
曲げを受けるピンの許容曲げ応力度は（5.9）式の値とする。
\(f_{b2}=F/1.1\) …(5.10)式
F：基準強度 (N/mm2)
※ただしこの記事を書いている私自身も”曲げを受けるピン”が示す意味が分かりません。このような知恵袋の記事もありますが理解できませんでした。
ピンの意味するものがピン梁、ピン接合、ピンetc… 様々考えられ想像できません。もし意味を説明できる方がいればコメントいただけると幸いです。
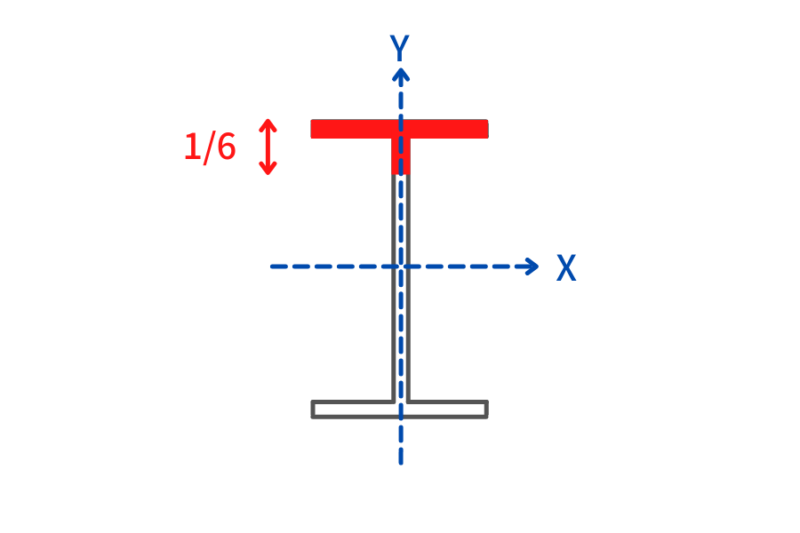
曲げ応力用の断面２次半径ib
曲げ応力用の断面２次半径ibは圧縮フランジ梁せいの1/6からなる断面のウェブ軸周りの断面二次半径を指します。
JIS材などの一般的な鋼材であれば機械的性質を調べると参考書に数値の記載があります。
計算の仕方などの詳しい解説はこちらの記事を参考にしてみて下さい。
限界細長比 Λ
[限界細長比]
\(Λ=\sqrt{\dfrac{\pi^2 E}{0.6F}}\)
E:ヤング係数(N/mm2)
F:基準強度(N/mm2)
限界細長比の詳しい解説はこちらの記事を参考にしてみて下さい！
基準強度 F値
基準強度F値は鋼材の種類によって異なります。
例えばSS400の鋼材(40㎜以下)であればF値が235N/mm2になるので
長期許容引張応力度 156.6N/mm2
短期許容引張応力度 235N/mm2
SN490の鋼材(40㎜以下)であればF値が325N/mm2になるので
長期許容引張応力度 216.6N/mm2
短期許容引張応力度 325N/mm2
基準強度F値についての詳しい解説はこちらの記事を参考にしてみて下さい。
長期と短期について
許容応力度は長期と短期で変わります。
長期とは長期間作用する荷重の合計つまり固定荷重や積載荷重など長期的に作用するものの合計したものを指します。
短期とは短期間作用する荷重の合計例えば地震や台風などの長期に加え短期的にも作用するものの合計したものを指します。
設計では長期許容曲げ応力度はLfb, 短期許容曲げ応力度はSfbで表すことがあります。
新規準(2005年)-許容曲げ応力度
新規準は旧規準に比べとても複雑です。旧規準式は建築基準法に取り入れられ社会的に浸透しているため従来通り使用することは可能です。今後、新規準式が浸透しシフトしていくと思われます。
ここでは本質と少しづれてしまいかなり説明が長くなるので新規準式については別の記事を用意していますのでこちらの記事を参考にしてみて下さい。
許容曲げ応力度の曲線
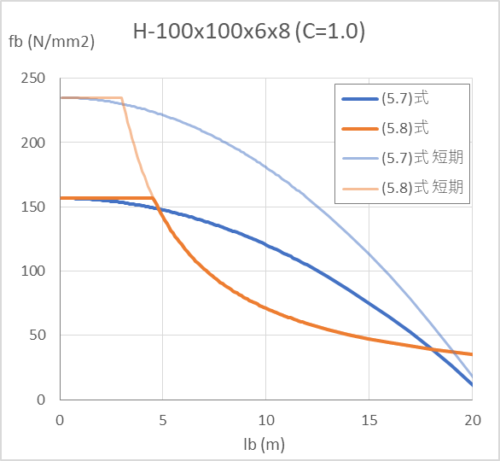
このグラフは許容曲げ応力度と座屈長さ(補剛間隔)の関係を表したグラフです。(C=1.0 F=235 E=205000 H-100x100x6x8の場合)
グラフを描くことで座屈長さが長くなるにつれて許容曲げ応力度はちいさくなることがわかります。また座屈長さが変わることで（5.7式）と（5.8式）のどちらが大きくなるかが一目瞭然となります。
ただしCの値や部材サイズによってグラフの形は様々なので一括りにどちらが大きくなるかはその都度、計算する必要があります。
共通して言えることは短期は長期の1.5倍になり、短期・長期ともに引張応力度ftの長期なら156.6N/mm2 短期なら235N/mm2を超えることはできません。
許容応力度検定
許容応力度検定は許容応力度に対して部材の負担する応力度が上回らないかを検定することです。
構造設計では許容応力度分の応力度をよく検定比と呼びます。この検定比が1.0を上回らないことが許容応力度設計です。
[許容曲げ応力度検定]
\(\sigma_{b}<f_{b}\)
\(\dfrac{\sigma_{b}}{f_{b}}<1.0\)
σb：曲げ応力度 (N/mm2)
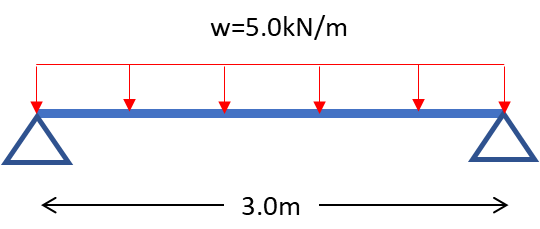
具体的な計算例を見ていきます。
梁材に長期の等分布荷重w=5.0kN/mをかけたときの応力度検定をします。
柱材はH-100x100x6x8 部材長さ3.0ｍ(横補剛材なし) 断面係数 Zx＝75.6cm3 曲げ応力用の断面二次半径 ib=27.5mm 材料をSS400材 ヤング係数E=205000N/mm2とします。簡易的な計算とするため自重は今回無視します。
まず部材に作用する曲げモーメントは
\(M=wl^2/8=5.0\cdot 3.0^2 / 8=5.63\)
つぎに部材に作用する曲げ応力度は
\(M/Z=5.63/ 75.6\cdot 1000=74.5\)
長期許容応力度fbを求めるためにまず細長比と限界細長比を求めます。
\(\lambda=l_{b}/i_{b}=3000/27.5=109.1\)
\(\Lambda=\sqrt{\dfrac{205000\pi^2}{0.6\cdot 235}}=119.7\)
（5.7式）で許容曲げ応力度を求めます。
\(f_{b1}=\left[\dfrac{2}{3}-\dfrac{4}{15C}\left(\dfrac{l_{b}/i_{b}}{\Lambda}\right)^2\right]\cdot F\)
\(f_{b1}=\left[\dfrac{2}{3}-\dfrac{4}{15*1.0}\left(\dfrac{109.1}{119.7}\right)^2\right]\cdot 235\)
\(f_{b1}=153.4\)
（5.8式）で許容曲げ応力度を求めます。
\(f_{b2}=\dfrac{89000\cdot A_{f}}{l_{b}\cdot h}\leq F/1.5\)
\(f_{b2}=\dfrac{89000\cdot 800}{3000\cdot 100}\leq 235/1.5\)
\(f_{b2}=156.6\)
（5.7式）（5.8式）のより大きいほうになるのでfb=156.6N/mm2
\(\dfrac{\sigma_{b}}{f_{b}}=\dfrac{74.5}{156.6}=0.48\) …OK
以上よりこの梁材は許容応力度以内に納まっているので許容応力度設計では問題ないことが確認できました。このように部材の設計を行っていきます。
まとめ
今回は許容曲げ応力度についてまとめてみました
許容応力度は構造設計をするうちで最も重要な値の一つです。この値を基準に部材サイズ・材質を決めたりしていきます。
一級建築士試験において許容曲げ応力度について問われることはほとんどありませんが、構造設計を生業とする場合は必ず覚えてください、というより切っても切れないほど多用するキーワードです。
許容曲げ応力度を確認する場合はぜひ本ブログを読み直してみて下さい！！
コメント