今回は露出柱脚のベースプレートの設計についてわかりやすく解説していきたいと思います。
私自身も露出柱脚の設計については設計するごとに頭を抱えるほど非常に重要かつ難しい設計のひとつです。しかしながら柱脚は建物の荷重を安全に地盤に反す役割があるため非常に大きい応力を負担する接合部です。したがって柱脚を正しく設計することは構造設計の中でも非常に重要なことです。
鋼構造を設計する際において露出柱脚は頻出の柱脚形式なので、ぜひこの記事を参考にしてみて下さい!!

露出柱脚の設計ってどうやるの??
露出柱脚の設計について

露出柱脚の設計は昔はよくピン柱脚(つまり曲げモーメントを負担しない柱脚)として設計されてきましたが、1996年の阪神淡路大震災で柱脚の被害が多かったことを機に回転剛性を加味し、曲げ応力を負担して設計するように求められています。
したがって露出柱脚は軸力(引張あるいは圧縮)、せん断力、曲げモーメントの3種類を用いて設計していきます。
ピン柱脚は柱脚が曲げモーメントを負担しないため柱頭に大きなモーメントが現れ、柱脚はモーメントがなし。つまり柱頭は安全側の設計、柱脚は危険側の設計となります。
半固定柱脚は柱脚が曲げモーメントを負担するため柱頭のモーメントが小さくなり、柱脚にはモーメントが現れます。つまり柱頭は危険側の設計、柱脚は安全側の設計となります。
完全なピン柱脚は存在しないことから考えると半固定柱脚の方が実状に合っているといえます。
露出柱脚の設計は検討項目が非常に複雑に分かれています。
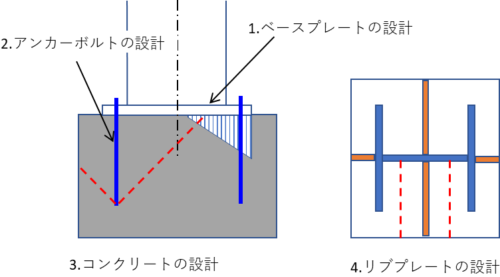
- ベースプレートの設計
- アンカーボルトの設計
- 柱型、基礎コンクリートの設計
- リブプレートの設計
1.ベースプレートの設計は圧縮応力による面外曲げの検討、引張応力による面外曲げの検討があります。
2.アンカーボルトの設計は引張力とせん断力に耐えうるかの検討があります。
3.柱型・基礎コンクリートの設計は引張力とせん断力によってコーン破壊しないかの検討があります。
4.リブプレートの設計はリブプレートが負担する範囲の圧縮応力に対して溶接部の検討があります。
以上だけでも非常に複雑かつ詳細な検討が多いことがわかっていただけたと思います。
今回の記事ではベースプレートの設計に焦点を絞って解説していきます。またほかの項目についても記事を更新していきますので、少々お待ちください。
ベースプレートの設計
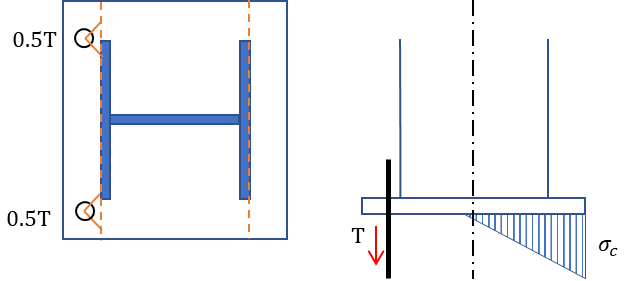
ベースプレートの設計項目は以下の通りです。
- 圧縮応力による面外曲げの検討
- アンカーボルトの引張応力による面外曲げの検討
圧縮応力による面外曲げの検討をするためには圧縮反力σcが必要になり、アンカーボルトによる面外曲げの検討するためにはアンカーボルトが負担する引張力Tが必要になります。これから紹介する算出方法でσcとTを求めていきます。
ベースプレートの曲げ応力の算出方法
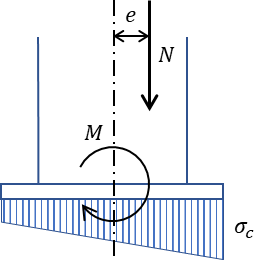
ベースプレートの曲げ応力を計算するためにまず偏心距離eを求めます。
さらに偏心距離eを使い、判別式からそれぞれに対応した式から圧縮反力σcとアンカーボルトの負担する引張力Tを求めていきます。
偏心距離eは柱脚にかかる軸力Nと曲げモーメントを使って以下の式によって求められます。
\(e=\dfrac{M}{N}\)
M:曲げモーメント (kN・mm)
N:軸力 (kN)
この記事ではN<0が引抜時とし、N<0のときe<0とします。またMは絶対値をとります。また正負が混在し不明瞭になるため、あえて絶対値記号を表記します。
つぎに判別式は以下のように分けられます。
- N>0 かつ e≦D/6 の場合
- N>0 かつ D/6<e≦D/6+d‘/3 の場合
- N>0 かつ D/6+d‘/3<e≦e3 の場合
- N>0 かつ e3<e の場合
- N=0 の場合
- N<0 かつ e2 ≦|e| の場合
- N<0 かつ 2(D/2-d’)2/D≦|e|<e2 の場合
- N<0 かつ 0<|e|<2(D/2-d’)2/D の場合
1. N>0 かつ e≦D/6 の場合
1.の場合は柱脚にかかる応力は圧縮力と相対的に小さい曲げモーメントが想定されます。
偏心距離の小さくベースプレートの断面の核の範囲に収まった場合、ベースプレートの全面圧縮時かつアンカーボルトは引張力を発生しない場合の検討になります。
\(\sigma_{c}=\dfrac{N}{BD}\left(1+\dfrac{6e}{D}\right)\)
\(T=0\)
B:ベースプレートの幅(曲げモーメントと直交方向の面)
D:ベースプレートのせい(曲げモーメントと平行方向の面)
2. N>0 かつ D/6<e≦D/6+d‘/3 の場合
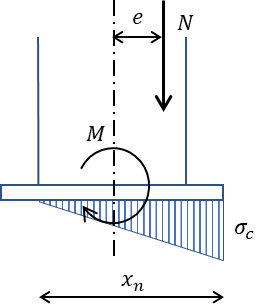
2.の場合は柱脚にかかる応力は圧縮力と少し大きめの曲げモーメントが想定されます。
偏心距離が小さくはないが大きくもない中程度であり、ベースプレートの断面の一部圧縮時かつアンカーボルトに引張力が発生しない場合の検討になります。
\(\sigma_{c}=\dfrac{2N}{3B\left(\dfrac{D}{2}-e\right)}\)
\(T=0\)
\(x_{n}=3\left(\dfrac{D}{2}-e\right)\)
B:ベースプレートの奥行幅
D:ベースプレートのせい(曲げモーメントと平行方向の面)
3. N>0 かつ D/6+d‘/3<e≦e3 の場合
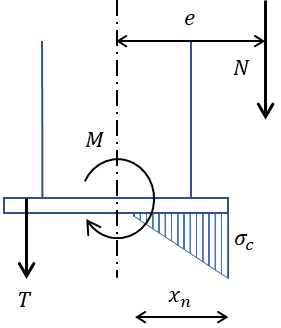
3.の場合は柱脚にかかる応力は圧縮力と大きめの曲げモーメント、または引張力と大きめの曲げモーメントが想定されます。
偏心距離が大きく、ベースプレートの断面の一部圧縮時かつ引張側アンカーボルトに引張力が発生する場合の検討になります。
\(x_{n}^3+3\left(e-\dfrac{D}{2}\right)x_{n}^2-\dfrac{6na_{t}}{B}\left(e+\dfrac{D}{2}-d’\right)(D-d’-x_{n})=0\)
\(\sigma_{c}=\dfrac{2N\left(e+\dfrac{D}{2}-d’\right)}{Bx_{n}\left(D-d’-\dfrac{x_{n}}{3}\right)}\)
\(T=\dfrac{N\left(e-\dfrac{D}{2}+\dfrac{x_{n}}{3}\right)}{D-d’-\dfrac{x_{n}}{3}}\)
B:ベースプレートの奥行幅
D:ベースプレートのせい(曲げモーメントと平行方向の面)
n:コンクリートに対する鋼材のヤング係数比 (n=15)
at:引張側アンカーボルトの軸部の総断面積
d’:ベースプレート端から引張側アンカーボルトまでの距離
4. N>0 かつ e3<e の場合
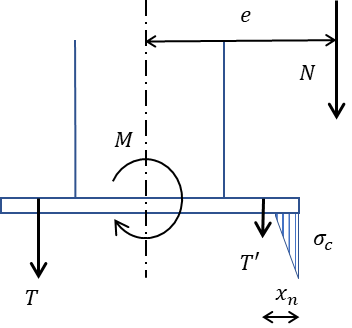
4.の場合は柱脚にかかる応力は圧縮力とさらに大きいの曲げモーメントが想定されます。
偏心距離がさらも大きく、ベースプレートの断面のごく一部圧縮時かつアンカーボルトすべてに引張力が発生する場合の検討になります。
\(x_{n}^3+3\left(e-\dfrac{D}{2}\right)x_{n}^2-\dfrac{12na_{t}}{B}\left[e\left(\dfrac{D}{2}-x_{n}\right)+\left(\dfrac{D}{2}-d’\right)^2\right]=0\)
\(\sigma_{c}=\dfrac{N}{Bx_{n}/2-na_{t}\dfrac{D-2x_{n}}{x_{n}}}\)
\(T=\dfrac{na_{t}N}{Bx_{n}/2-na_{t}\dfrac{D-2x_{n}}{x_{n}}}\dfrac{D-d’-x_{n}}{x_{n}}\)
\(T’=\dfrac{na_{t}N}{Bx_{n}/2-na_{t}\dfrac{D-2x_{n}}{x_{n}}}\dfrac{d’-x_{n}}{x_{n}}\)
B:ベースプレートの奥行幅
D:ベースプレートのせい(曲げモーメントと平行方向の面)
n:コンクリートに対する鋼材のヤング係数比 (n=15)
at:引張側アンカーボルトの軸部の総断面積
d’:ベースプレート端から引張側アンカーボルトまでの距離
ただし4.の場合が成り立つのはβが1未満の場合のみである。βが1以上の場合は3.になります。
\(e_{3}=\dfrac{\dfrac{-3na_{t}}{Bd’}\left(\dfrac{D}{d’}-2\right)^2-\dfrac{3D}{2d’}+1}{\dfrac{6na_{t}}{Bd’}\left(\dfrac{D}{d’}-2\right)-3}\cdot d’\)
\(\beta=\dfrac{2na_{t}}{Bd’}\left(\dfrac{D}{d’}-2\right)<1.0\)のとき\(e_{3}\)は存在する。\(e_{3}\)が存在しない場合は判別式3.とする。
5. N=0 の場合
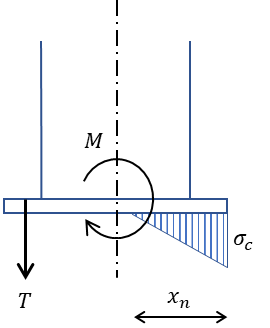
5.の場合は柱脚にかかる曲げモーメントのみになります。
偏心距離が計算できません、応力状態はベースプレートの断面の一部圧縮時かつアンカーボルトに引張力が発生する場合の検討になります。
\(x_{n}=\dfrac{na_{t}}{B}\left(-1+\sqrt{1+\dfrac{2B(D-d’)}{na_{t}}}\right)\)
\(\sigma_{c}=\dfrac{2M}{Bx_{n}(D-d’-x_{n}/3)}\)
\(T=\dfrac{M}{D-d’-x_{n}/3}\)
B:ベースプレートの奥行幅
D:ベースプレートのせい(曲げモーメントと平行方向の面)
n:コンクリートに対する鋼材のヤング係数比 (n=15)
at:引張側アンカーボルトの軸部の総断面積
d’:ベースプレート端から引張側アンカーボルトまでの距離
6. N<0 かつ e2≦|e| の場合
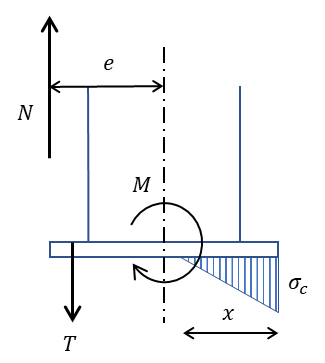
6.の場合は柱脚にかかる応力は引張力と大きめの曲げモーメントが想定されます。
偏心距離が大きく、ベースプレートの断面の一部圧縮かつ引張側アンカーボルトに引張力が発生する場合の検討になります。
\(x^3-3\left(|e|+\dfrac{D}{2}\right)x^2+\dfrac{6na_{t}}{B}\left(\dfrac{D}{2}-|e|-d’\right)x-\dfrac{6na_{t}}{B}\left(\dfrac{D}{2}-|e|-d’\right)(D-d’)=0\)
\(\sigma_{c}=\dfrac{|e|-D/2+d’}{D-d’-x/3}\cdot\dfrac{2}{Bx}|N|\)
\(T=\dfrac{|e|+D/2-x/3}{D-d’-x/3}|N|\)
B:ベースプレートの奥行幅
D:ベースプレートのせい(曲げモーメントと平行方向の面)
n:コンクリートに対する鋼材のヤング係数比 (n=15)
at:引張側アンカーボルトの軸部の総断面積
d’:ベースプレート端から引張側アンカーボルトまでの距離
またe2の計算式は以下のようになります。6.の場合が成り立つのはβが1以上の場合のみであり、βが1未満の場合は7.になります。
\(e_{2}=\dfrac{\dfrac{3na_{t}}{Bd’}\left(\dfrac{D}{d’}-2\right)^2+\dfrac{3D}{2d’}-1}{\dfrac{6na_{t}}{Bd’}\left(\dfrac{D}{d’}-2\right)-3}\cdot d’\)
7. N<0 かつ 2(D/2-d’)2/D≦|e|<e2 の場合
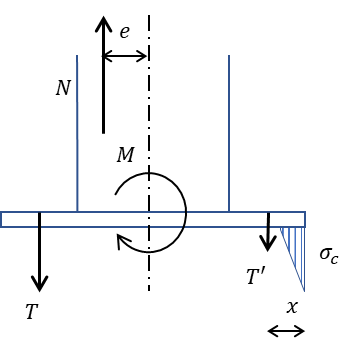
7.の場合は柱脚にかかる応力は引張力と曲げモーメントが想定されます。
偏心距離が中程度でベースプレートの断面の局部圧縮かつアンカーボルトすべてに引張力が発生する場合の検討になります。
\(x^3-3\left(|e|+\dfrac{D}{2}\right)x^2-\dfrac{12na_{t}|e|}{B}x+\dfrac{6na_{t}}{B}\left[D\left(|e|+\dfrac{D}{2}\right)-\left(D-d’\right)^2-d’^2\right]=0\)
\(\sigma_{c}=\dfrac{|N|}{-Bx/2+na_{t}\dfrac{D-2x}{x}}\)
\(T=na_{t}\sigma_{c}\dfrac{D-d’-x}{x}\)
\(T’=na_{t}\sigma_{c}\dfrac{d’-x}{x}\)
B:ベースプレートの奥行幅
D:ベースプレートのせい(曲げモーメントと平行方向の面)
n:コンクリートに対する鋼材のヤング係数比 (n=15)
at:引張側アンカーボルトの軸部の総断面積
d’:ベースプレート端から引張側アンカーボルトまでの距離
8. N<0 かつ 0≦|e|≦ 2(D/2-d’)2/D の場合
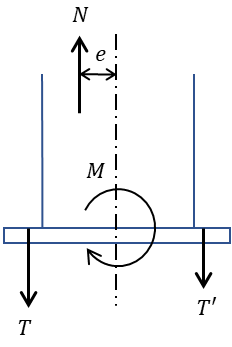
8.の場合は柱脚にかかる応力は引張力と小さめの曲げモーメントが想定されます。
偏心距離が小さく、ベースプレートにかかる圧縮はなくかつアンカーボルトすべてに引張力が負担する場合の検討になります。
\(T=(0.5+\dfrac{|e|}{D-2d’})|N|\)
\(T’=(0.5-\dfrac{|e|}{D-2d’})|N|\)
D:ベースプレートのせい(曲げモーメントと平行方向の面)
d’:ベースプレート端から引張側アンカーボルトまでの距離
上記の数式は基本的にアンカーボルトが4隅に一本ずつの場合の時のみに成り立ちます。
アンカーボルト4本以上のベースプレートの計算は変わりますが参考図書もないため、設計者判断になります。別の方法として、既製品柱脚を使うと比較的簡単です。
圧縮反力による面外曲げの検討
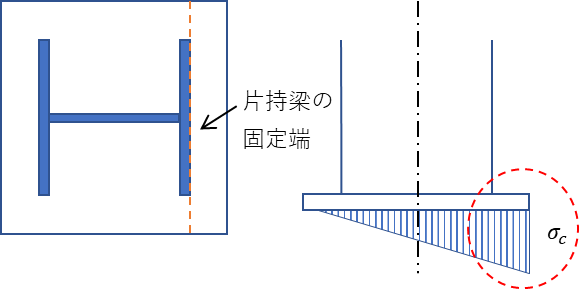
ここまでで判別式とベースプレートにかかる応力を求めることができます。次は圧縮反力による面外曲げの検討を行います。
求めたベースプレートに作用する圧縮反力σcから固定端までの距離を用いて曲げモーメントを算出し、ベースプレートのもつ許容曲げ応力度fbを上回らないことを確認します。
曲げモーメントはベースプレートの形状、リブプレートの有無によって検討項目が変化します。
ここではその形状の一例を紹介します。
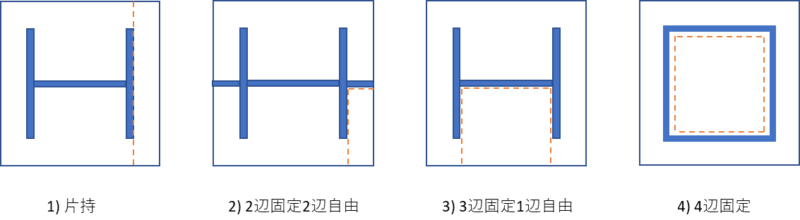
- 片持梁としての検討
- 2辺固定端2辺自由端としての検討
- 3辺固定端1辺自由端としての検討
- 4辺固定端としての検討
1.片持梁としての検討 は等分布荷重を受ける片持ち梁と同じように計算します。
\(M=\dfrac{1}{2}\sigma_{c}l^2\)
\(\sigma_{c}\)は算出した圧縮反力です。実際には応力勾配があるので台形分布となりますが計算を単純化するため最大圧縮反力を等分布荷重とみなして計算します。
\(l\) は固定端から自由端(ベースプレート端)までの距離となります。
曲げモーメントの算出方法についての詳しい解説はこちらの記事を参考にしてみて下さい。
2.~4. の場合は長方形スラブの応力図表から曲げモーメントMを求めます。
\(l_{x}\)は短い方の固定端から自由端(ベースプレート端)までの距離\(l_{y}\)は長い方の固定端から自由端(ベースプレート端)までの距離となります。
\(\dfrac{l_{y}}{l_{x}}\)を求め、図表から曲げモーメントMを求めます。
Mが求まったら次に断面係数Zを求めます。Zは単位幅つまり1mm幅での断面係数とします。計算式は以下になります。
[断面係数Z]
\(Z=\dfrac{t^2}{6}\)
t:ベースプレート厚さ(mm)
曲げモーメントMと断面係数Zを求めることができたので曲げ応力度σbを求め、さらにベースプレートの許容曲げ応力度fbと比較することでベースプレートの許容応力度設計ができます。
曲げ応力度σbと許容曲げ応力度fbは以下になります。
[曲げ応力度σb]
\(\sigma_{b}=\dfrac{M}{Z}\)
[許容曲げ応力度fb]
\(f_{b}=\dfrac{F}{\nu}\)
[許容応力度設計]
\(\dfrac{\sigma_{b}}{f_{b}}≦1.0\)
F:基準強度
ν:長期=1.5 短期=1.0
アンカーボルトの引張力による面外曲げの検討
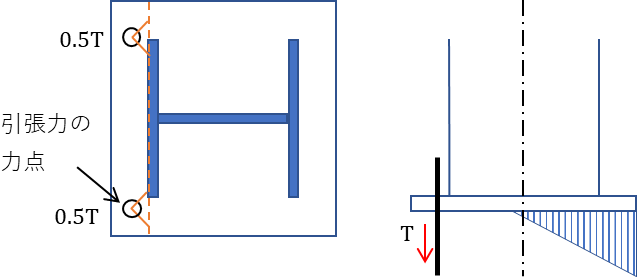
アンカーボルトの引張力による面外曲げの検討は先ほど求めたアンカーボルトに作用する引張力Tから固定端までの距離を用いて曲げモーメントを算出し、ベースプレートのもつ許容曲げ応力度fbを上回らないことを確認します。
曲げモーメントはアンカーボルトから固定端までの距離、リブプレートの有無によって変化します。
ここではその形状の一例を紹介します。
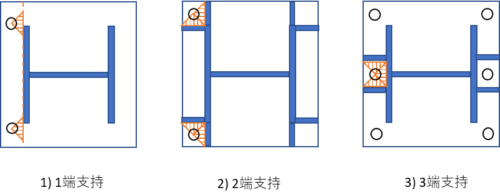
- 1端支持としての検討
- 2端支持としての検討
- 3端支持としての検討
アンカーボルトの中心を力点として考え、そこから柱端部までの距離を \(l\) とします。
引張力は45°方向の加力線にそって応力分配できると仮定し、協力幅b’において断面検討を行います。
曲げモーメントの算出方法は引張側のアンカーボルト本数ntで引張力Tを除する必要があります。
\(M=\dfrac{T}{n_{t}}\cdot l\)
Mが求まったら次に断面係数Zを求めます。Zは協力幅で断面係数を使います。計算式は以下になります。
[協力幅b’]
\(b’=2l\cdot i\)
i:支持端の数 1端支持ならばi=1
※B.PLの形状、A.Bolt、Rib.PLの配置によっては上記の式によらず実状に沿ったb’を設定すること
[断面係数Z]
\(Z=\dfrac{b’\cdot t^2}{6}\)
t:ベースプレート厚さ(mm)
曲げモーメントMと断面係数Zを求めることができたので曲げ応力度σbを求め、さらにベースプレートの許容曲げ応力度fbと比較することでベースプレートの許容応力度設計ができます。
曲げ応力度σbと許容曲げ応力度fbは以下になります。
[曲げ応力度σb]
\(\sigma_{b}=\dfrac{M}{Z}\)
[許容曲げ応力度fb]
\(f_{b}=\dfrac{F}{\nu}\)
[許容応力度設計]
\(\dfrac{\sigma_{b}}{f_{b}}≦1.0\)
F:基準強度
ν:長期=1.5 短期=1.0
おすすめの参考書
上記の図書は鋼構造設計の基本的な設計方法を示したもので柱脚の設計の一部が記されたもので、鋼構造設計の基本を学びたいひとは購入を考えてみてください!!
上記の図書は非常に細かく柱脚の設計から施工までを記されたもので、ここにしか載っていないグラフもあるので柱脚を詳しく知りたい方は購入を考えてみてください!!
「鋼構造の性能と設計」はベースプレートの曲げ引張りに関しての記載のある唯一の書籍です。リンクは正しいですが画像は「免疫研究の最前線」となっており間違っています。ご確認の上ご購入下さい。
お知らせ
露出柱脚の応力算定シートを作成しました。
有料にはなりますが、皆様の設計の一助となれば幸いです。ぜひダウンロードしてください!!
まとめ
今回は露出柱脚のベースプレートの設計方法についてまとめてみました。
ベースプレートの設計は構造設計のなかでも個人的に最も難しいと思う設計法です。
構造設計を生業とするひとは必ずつまづく問題です。ここまで詳しく記載したブログはほかにないと思います。ぜひ算出過程をこのブログで覚えていってください!!


コメント
構造設計の仕事をしていまして、露出柱脚の設計について拝見させて頂きました。
露出柱脚の設計で、曲げ圧縮が生じた場合の設計方法は色々な書籍に記載があるのですが、
曲げ引張が生じている場合については、なかなか記載がなく困っていました。
このブログでは細かく書かれているので、勉強になります。
日本建築士事務所協会連合会の出版の構造設計Q&A集に、曲げ引張についての説明があったのですが、ここに書かれているものとは異なっていました。
申し訳ありませんが、ここに記載されている曲げ引張の計算方法の出典元をご教示いただけないでしょうか。
コメントありがとうございます。
私も同じように曲げ引張りの問題によく直面し、書籍を探していたところ
「綱構造の性能と設計」桑村仁 著 という書籍に
曲げ引張りの記述を見つけました、こちらを参照しています。
おそらく唯一の書籍になると思います。
本ブログではeの絶対値をとり、正負を逆転させている箇所もごさいますが、最終的な数値が同じになることを確認しております。
リンクをブログ内で添付いたします。
ありがとうございます。参考にさせて頂きます。
booth にて1000円でベースプレート検討のエクセルを購入しました。
下記の場合に、#NAME?となって結果が表示されません。
理由や改善方法をご教示いただけませんでしょうか。
よろしくお願い申し上げます。
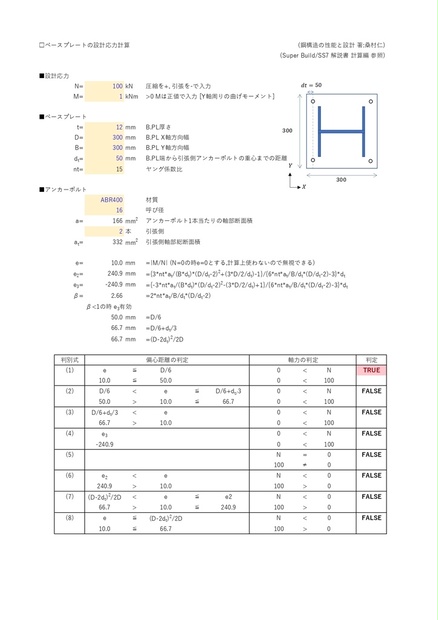
□ベースプレートの設計応力計算 (鋼構造の性能と設計 著:桑村仁)
(Super Build/SS7 解説書 計算編 参照)
■設計応力
N= 11.5 kN 圧縮を+, 引張を-で入力
M= 22.56 kNm >0 Mは正値で入力 [Y軸周りの曲げモーメント]
■ベースプレート
t= 25 mm B.PL厚さ
D= 450 mm B.PL X軸方向幅
B= 450 mm B.PL Y軸方向幅
dt= 50 mm B.PL端から引張側アンカーボルトの重心までの距離
nt= 15 ヤング係数比
■アンカーボルト
SS400 材質
25 呼び径
a= 507 mm2 アンカーボルト1本当たりの軸部断面積
2 本 引張側
at= 1014 mm2 引張側軸部総断面積
e= 1961.7 mm =|M/N| (N=0の時e=0とする,計算上使わないので無視できる)
e2= 220.3 mm ={3*nt*at/(B*dt)*(D/dt-2)2+(3*D/2/dt)-1}/{6*nt*at/B/dt*(D/dt-2)-3}*dt
e3= -220.3 mm ={-3*nt*at/(B*dt)*(D/dt-2)2-(3*D/2/dt)+1}/{6*nt*at/B/dt*(D/dt-2)-3}*dt
β= 9.46 =2*nt*at/B/dt*(D/dt-2)
β<1の時 e3有効
75.0 mm =D/6
91.7 mm =D/6+dt/3
136.1 mm =(D-2dt)2/2D
判別式 偏心距離の判定 軸力の判定 判定
(1) e ≦ D/6 0 75.0 0 < 11.5
(2) D/6 < e ≦ D/6+dt/3 0 < N FALSE
75.0 91.7 0 < 11.5
(3) D/6+dt/3 < e 0 < N TRUE
91.7 < 1961.7 0 < 11.5
(4) e3 0 < N FALSE
-220.3 0 < 11.5
(5) N = 0 FALSE
11.5 ≠ 0
(6) e2 < e N < 0 FALSE
220.3 0
(7) (D-2dt)2/2D < e ≦ e2 N < 0 FALSE
136.1 220.3 11.5 > 0
(8) e ≦ (D-2dt)2/2D N 136.1 11.5 > 0
_img3
■(1) e≦D/6の時 FALSE
σc= — N/mm2
■(2) D/6<e≦D/6+dt/3の時 FALSE
xn2= — mm
σc= — N/mm2
■(3) D/6+dt/3<e≦e3の時 TRUE 1 5210.217391 433330.6957 -173332278.3
xn3= #NAME? mm
σc= #NAME? N/mm2
T= #NAME? kN T/nt= #NAME? kN/本
■(4) e3<eの時 FALSE 1 5210.217391 795681.3913 -191449813
xn4= — mm
σc= — N/mm2
T= — kN T/nt= — kN/本
T'= — kN T'/nt= — kN/本
■(5) N=0の時 FALSE
xn5= — mm
σc= — N/mm2
T= — kN T/nt= — kN/本
■(6) e2<eの時 (N<0) FALSE 1 -6560.217391 -362350.6957 144940278.3
xn6= — mm
σc= — N/mm2
T= — kN T/nt= — kN/本
■(7) (D-2dt)2/2D<e≦e2の時 (N<0) FALSE 1 -6560.217391 -795681.3913 166606813
xn7= — mm
σc= — N/mm2
T= — kN T/nt — kN/本
T'= — kN T'/nt= — kN/本
■(8) e≦(D-2dt)2/2Dの時 (N<0) FALSE
T= — kN T/nt= — kN/本
T'= — kN T'/nt= — kN/本
ご購入ありがとうございます。
まず考えられるのは、アンカーボルトサイズの25は想定していないので、エラーになるかもしれません
私のメールアドレスにEXCELを送付いただければ確認いたします。
しかしながらお時間いただくかもしれません
よろしくお願いします
ttb.abc.ln7@gmail.com
いつも勉強させていただいております。
2軸曲げの場合、それぞれの軸に対して上記の計算を行う認識でよろしいでしょうか。
ご教示いただけますと幸いです。
柱脚2軸曲げに対しては具体的な文献がないので
我々設計者も設計には苦慮しております。
実務では強軸曲げの検定比と弱軸曲げの検定比を足し合わせことで簡易的に求めることが多いです。安全側の設計になるため
但し、検定比は大きく出るので過剰設計になることもあります。
基礎フーチングの2軸曲げの検討を参考にすることもあります。
正確にやろうとするならばFEM解析で柱脚をモデル化して応力度を求める他ないようです。
ご返信いただき、ありがとうございます。
参考にさせていただきます。
強度計算の仕事をしていることがあり、
露出柱脚の設計についての箇所を拝見させていただきました。
上記において『5. N=0 の場合』の式を挙げていただいていますが、
その部分の根拠となる出典を私自身が探すことができておりません。
もし開示いただくことが可能であれば、その出典などをご教授いただけないでしょうか。
お手数おかけしますが、よろしくお願いいたします。
ユニオンシステム様のss7のマニュアルになります。
お手数をおかけしますがよろしくおねがいします。