切断法とは

今回は切断法についてわかりやすく解説していきたいと思います。

一級建築士試験におけるトラスの問題は節点法と切断法を用いる頻出問題です。今回はそのひとつの切断法についてまとめたいと思います。

節点法についても記事がありますので、ぜひ参考にしてみて下さい。

節点法とは

切断法とは

切断法とは軸力を求めたい部材を切断しモーメントのつり合い式から軸力を求めることができる方法を指します

切断法のメリットは軸力を求めたい部材をすぐに求められる点

切断法のデメリットは切断できる軸力の未知数が4つ以上になると解くことが不可能な点

したがって切断できる箇所は自然と決まるので複雑なトラスには切断法が使えません

軸力０の部材の見つけ方

トラスにおける軸力０の部材を見つける方法として節点を直線につなぐトラス構造には法則があります。この法則をつかう条件は

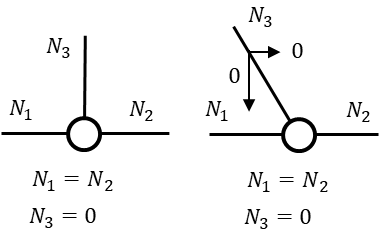
上記の図の場合でみると直線上の２つの部材の軸力（引張・圧縮力）は力のつり合い式によって常につり合うため

\(N_{1}=N_{2}\)

対して直角方向（図の場合は鉛直方向）の力が0でないと、力のつり合い式が成立しないためN₃の軸力は必ず０になります。（斜めに取りつく場合でもN₃の軸力は０）

\(N_{3}=0\)

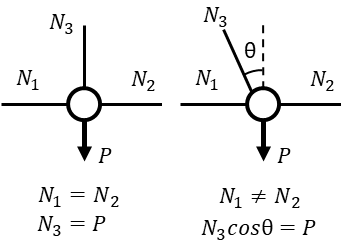
①節点には荷重（外力）が作用する場合かつ②3つ目の部材が直角に取りつく場合は

直線上の部材の軸力（引張・圧縮力）は常につり合い、直角方向（図は鉛直方向）の力がPでないと力のつり合い式が成り立たないため\(N_{3}\)（直線上にない部材）の軸力は常に荷重Pと一致します。

\(N_{1}=N_{2}\)
\(N_{3}=P\)

3つ目の部材が斜めに取りつく場合は直角方向の力がPになるように力のつり合い式を求めると

\(N_{3}\cos\theta=P\)

一方で\(N_{3}\)の水平成分の力が発生することにより

\(N_{1}≠N_{2}\)

となるので注意しましょう！

切断法の解き方

切断法の解き方は

1. 支点反力をもとめる
2. 部材を仮想的に切断する
3. 求めたい軸力を計算できる節点からモーメントのつり合い式を求める
4. 求めたい軸力があれば3の繰り返し

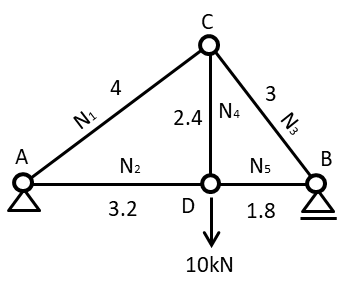
ここで例題を見ながら解いてみましょう

D点に10kNの荷重が作用しているモデルを想定します

部材ごとの軸力を(N₁、N₂…)のように仮に定義しておきます

1.支点反力を求める

まずは支点反力を求めます

A点、B点それぞれの反力をRa、Rbとします

水平方向の力つり合い式ΣH=0はB点ローラー支点とわかればA点の水平反力は0と瞬時に判断しましょう

鉛直方向の力つり合い式ΣV=0は

\(Ra+Rb=10\)　…(1)

A点まわりのモーメントのつり合い式ΣMa=0は

\(10\times3.2-5\times Rb=0\) …(2)

(1)(2)式を計算すると

\(Ra=3.6\)
\(Rb=6.4\)

と求まりました

（支点反力を求めるの節点法および切断法ともに共通です）

2.部材を仮想的に切断する

つぎに部材を仮想的に切断します

切断の方法は①求めたい部材の軸力を切ることと②4本以上部材を切断しないことです

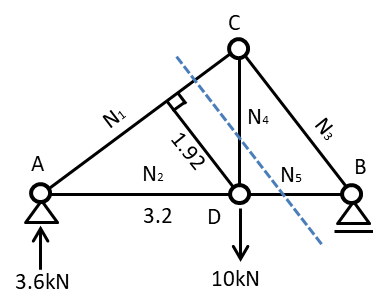
もし仮にN₁の軸力を求めたいときにはN₁を切るように切断線を引きます

図では赤線と青線で引きましたどちらでも解けますが

赤線の場合は解き方が節点法とおなじになるため

今回は青線のように切断した時を想定します

節点法の解き方はこちら

3.求めたい軸力を計算できる節点からモーメントのつり合い式を求める

つぎに求めたい軸力を計算できる節点からモーメントのつり合い式を求めます

ここでいう『求めたい軸力を計算できる節点』とは

N₁を求めたいときはN₄,N₅の交点となる節点つまりD点が条件の合う節点です

逆に

N₄を求めたいときはN₁,N₅の交点の節点A

N₅を求めたいときはN₁,N₄の交点の節点C

つまり

求めたい軸力以外の未知数の部材の交点からモーメントのつり合いをつくります

N₁：D点まわりのモーメントのつり合い

\(3.6kN\times 3.2-N_{1}\times1.92=0\)
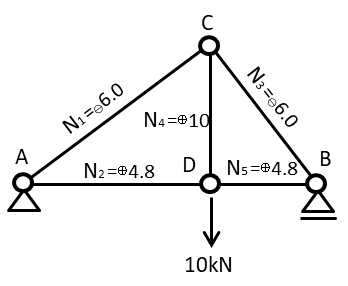
\(N_{1}=6kN\) (圧縮⊖)

N₄：A点まわりのモーメントのつり合い

\(10kN\times 3.2-N_{4}\times3.2=0\)
\(N_{4}=10kN\) (引張⊕)

N₅：C点まわりのモーメントのつり合い

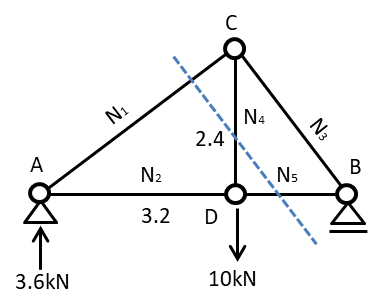
\(3.6kN\times 3.2-N_{5}\times2.4=0\)
\(N_{5}=4.8kN\) (引張⊕)

ここまでで紹介した方法でN₂とN₃についても解けると思いますので

練習がてら解いてみるとよいのではないでしょうか！？

具体的な問題

最後に実際にあった一級建築士試験の節点法の問題から解いてみましょう

節点法の問題

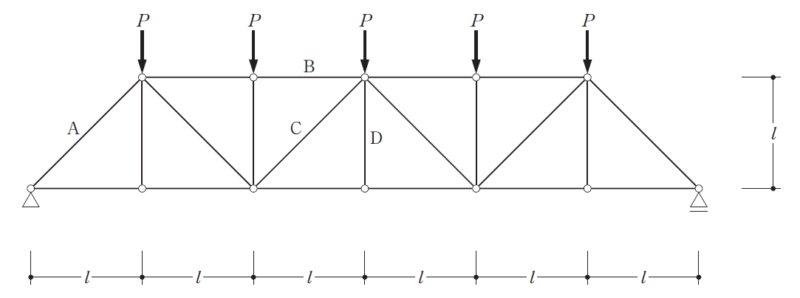
[問題]

部材A・B・C・Dの軸力を求める問題です

このような問題は節点法より切断法のほうが解くスピードは速くなります

先ほど説明した切断法の解き方で早速解いてみましょう！

[計算過程]

1.軸力０部材を洗い出す

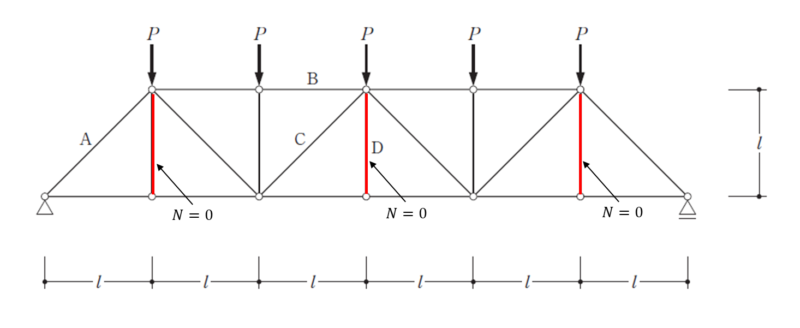
まずは軸力０の部材は最初に探しておきます。先ほど紹介した軸力０の見つけ方を適用すると

直線となる2つの部材とそれに取りつく1つの部材で構成されている箇所は３つ該当するので、したがって\(N_{D}=0\)となることがわかりました

2.支点反力を求める

つぎはトラスの支点反力を求めます

水平反力は片側ローラー支点かつ水平荷重がないので０と瞬時にわかります

鉛直反力もシンメトリー(対称軸を持つ)モデルなので左右の反力は同じになるので

\(R_{1}=R_{2}=\dfrac{5}{2}P\)

つぎに切断箇所を決めます

3.切断法で軸力を算定する

つぎからは順次、切断法を行い軸力を算定します。

1回ではすべての軸力が求まらないので数回に分けます、まずはAの軸力を求めたいので部材Aを切ります。

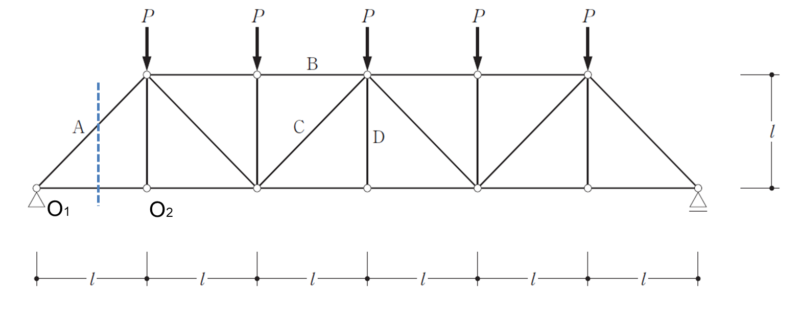
N_A：O₂点まわりのモーメントのつり合い

\(\dfrac{5}{2}P\times l-N_{A}\times\dfrac{l}{\sqrt{2}}=0\)

\(N_{A}=\dfrac{5\sqrt{2}}{2}P\)

N_Aを節点を押し込む向きに設定し

つぎにB・Cの軸力を求めたいのでB・C・E部材を切り、N_Bを求めるためCとEの交点O₃からつり合い式を出します

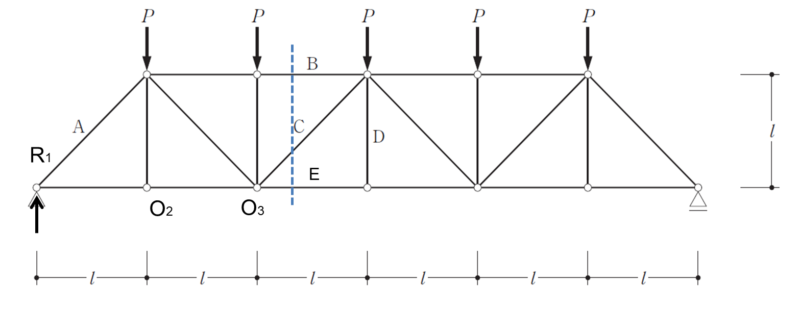
N_B：O₃点まわりのモーメントのつり合い

\(\dfrac{5}{2}P･2l-P･l-N_{B}･l=0\)

\(N_{B}=4P\)

N_Bを節点を押し込む向きに設定したので圧縮力となります。

つぎにCの軸力を求めたいので未知数Eの直線上で任意点のO₂からつり合い式を出します

N_C：O₂点まわりのモーメントのつり合い

\(\dfrac{5}{2}P･l+P･l-N_{B}･l+N_{C}･\dfrac{l}{\sqrt{2}}=0\)

\(N_{C}=\dfrac{\sqrt{2}}{2}P\)

これですべての軸力がわかりました

答えは『N_A=5√2P/2(圧縮),N_B=4P(圧縮),N_C=√2P/2(圧縮),N_D=0』となります

もちろん節点法による解き方もありますのでトライしてみて下さい！！

節点法とは

まとめ

今回は切断法についてまとめてきました

一級建築士試験でも頻出の問題です

切断法は支点反力を求めて、未知数が3つ以下になるように切断し軸力のを求める方法です

切断のしかたやモーメントのつり合い式をたてる基点の置き方、ベクトルの向きの置き方に少し癖があります

イメージがつかみにくいですがマスターすれば求めたい軸力をすぐに求められて便利です

習得できるようにこの記事を何度も見て勉強してください！！それでは！！