今回は建築で使われる風荷重についてわかりやすく解説していきたいと思います。
風荷重は建築の構造設計を行う上で重要な要素です。ぜひこの記事を参考にしてみて下さい!!

風荷重・風圧力ってなんだ??
こちらの記事は建築基準法施行令第87条および建設省告示1458号を参照しています。
風荷重とは

風荷重(英:Wind Load)とは建物の形状ないしは風の向き、あるいは部材の形状によって変化する風荷重の大きさを係数で表した値です。
例えば同じ風でも風上と風下を比較すると風が先にあたる風上の方が大きく風下は小さくなることがイメージできるかと思います。
したがって同じ速度圧(風速)であっても建物形状や風の当たる場所によって建物に与える荷重の大きさ変化すると覚えておいてください。
風荷重の記号は[W]や[W.L]で表し、単位は力の[N],[kN]です。風荷重を式で表すと
[風荷重・風圧力]
\(W=p\cdot A\)
\(\omega=Cf\cdot q\)
A:受風面積(m2)
ω:単位面積当たりの風圧力(N/m2)
Cf:風力係数
q:速度圧(N/m2)
速度圧の求め方
速度圧は国土交通大臣が定める方法で算出した値と基準風速から求めることができ、風圧力の算定に用います。
速度圧は記号は[q]で表し、単位は力/面積の[N/m2],[kN/m2]です。算定式は
[速度圧]
\(q=0.6E\cdot V_{0}^2\)
E:国土交通大臣が定める方法で算出した値
V0:基準風速(m/s)
基準風速は建物を建てる(あるいは建っている)その地方・場所により決定されます。
基準風速はこちら
国土交通大臣が定めるEの求め方
Eは国土交通大臣が定める方法で算出した値のことを指します。具体的にはその地方のガスト影響係数と地表面粗度区分から求めることができ、速度圧の算定に必要な値です。算定式は
[国土交通大臣が定める値 E]
\(E=E_{r}^2\cdot G_{f}\)
Er:平均風速の高さ方向の分布を表す係数
Gf:ガスト影響係数
平均風速の高さ方向の分布を表す係数 Er
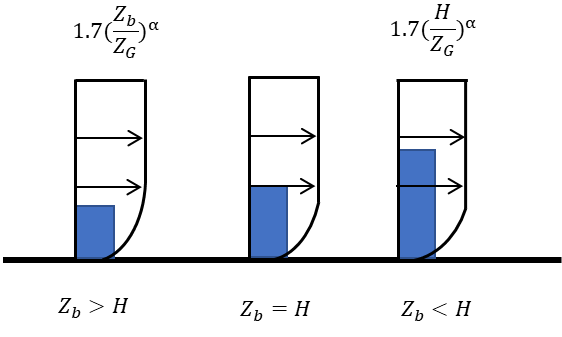
平均風速の高さの分布を表す係数は粗度区分から算定される値で建物の高さと地表面粗度区分によって変わる係数です。建物高さHが大きくなればなるほど値は大きくなり、地表面粗度区分が地表面が粗くなるほど小さくなる傾向にあります。
平均風速の高さの分布を表す係数の記号は[Er]で表記され、単位は無次元です。平均風速の高さの分布を表す係数の基本値は以下の式で求めらます。
[平均風速の高さ方向の分布を表す係数Er]
H≦Zbの場合
\(Er=1.7\left(\dfrac{Zb}{Z_{G}}\right)^\alpha\)
H>Zbの場合
\(Er=1.7\left(\dfrac{H}{Z_{G}}\right)^\alpha\)
H:建築物の高さと軒の高さの平均(m)
Zb,ZG及びα:粗度区分に応じて定められる数値
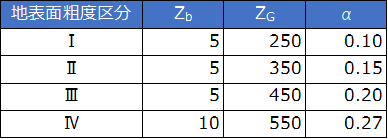
計算例として地表面粗度区分をⅡ、建築物高さH=20mとした場合
\(H=20>Zb=5\)なので適用する式は
\(Er=1.7\left(\dfrac{H}{Z_{G}}\right)^\alpha\)
\(Er=1.7\left(\dfrac{20}{350}\right)^{0.15}\)
\(Er=1.11\)
ガスト影響係数 Gf
ガスト影響係数(英:Gust effect factor)は同じく粗度区分から算定される値で風の乱れや風の変動の影響を考慮した割り増し係数になります。
ガスト影響係数の値は1.8~3.1の間で推移するので平均風速の2,3倍程度は大きく安全性が保たれるように規定されていることがわかります。また建築物高さHが低いものの方が係数が大きくなるので低層建築物の方が風の乱れの影響が大きいこともわかります。
ガスト影響係数の記号は[Gf]で表記され、単位は無次元です。ガスト影響係数の値は下記の表から読み取ります。

建築物高さHが(二)に該当する(10m以上、40m以下)場合は直線補間を行う必要があるのでその際は以下の式を使って下さい
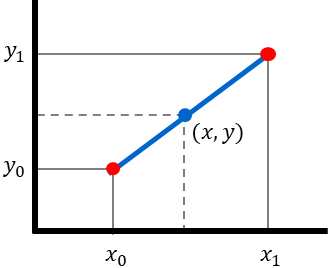
求めたい値をy,建築物高さx=Hとすると
\(y=y_{0}+(y_{1}-y_{0})\dfrac{x-x_{0}}{x_{1}-x_{0}}\)
例えば粗度区分ⅡでH=20mとしたら
\(y=2.2+(2.0-2.2)\dfrac{20-10}{40-10}\)
\(y=2.13\)
地表面粗度区分についてはこちらの記事を参考にしてみて下さい
地表面粗度区分とは
風力係数
風力係数とは建物の形状ないしは風の向き、あるいは部材の形状によって変化する風荷重の大きさを係数で表した値です。
例えば同じ風でも風上と風下を比較すると風が先にあたる風上の方が大きく風下は小さくなることがイメージできるかと思います。
したがって同じ速度圧(風速)であっても建物形状や風の当たる場所によって建物に与える荷重の大きさ変化すると覚えておいてください。
風力係数の記号は[Cf]で表し、単位は無次元です。
風力係数は以下の記事で詳しく解説していますので、そちらを参照してください。
風力係数とは(閉鎖型・開放型)
風力係数とは(独立上屋・ラチス構造物)
風荷重の計算例
ここで風荷重の具体的な計算例を示します。
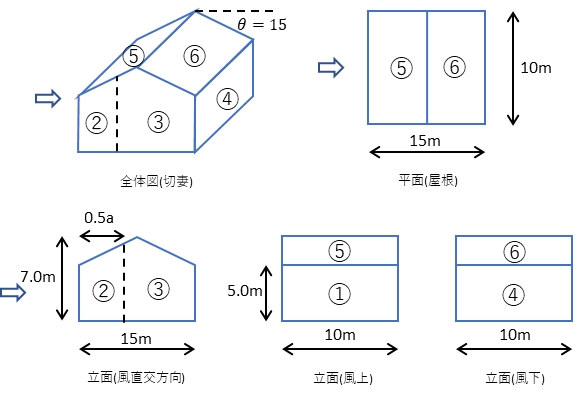
- 切妻屋根・閉鎖型の建物
- B=10m D=15m
- 地表面粗度区分Ⅲ
- 場所は東京23区内
- 建築物の高さと軒の高さとの平均H=6m
- 当該部分の地盤面からの高さはZ=7mとする
- 屋根勾配15度
1.風力係数を求める
風力係数の求め方は複雑なので今回は以前紹介した記事の風力係数を流用します。
詳しい風力係数の解説についてはこちらの記事を参考にしてください。
風力係数とは(閉鎖型・開放型)
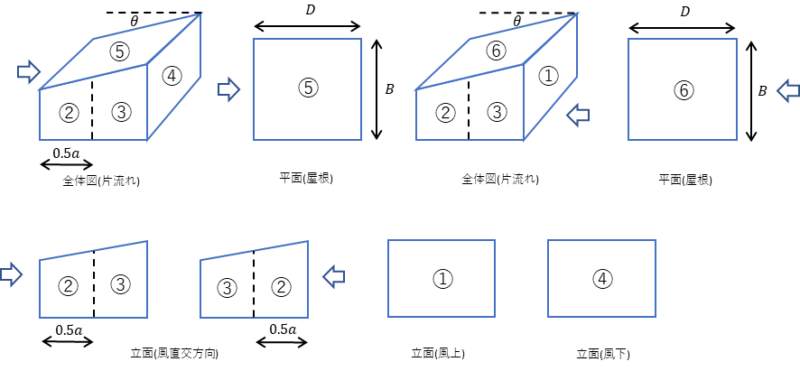
張間方向の風力係数
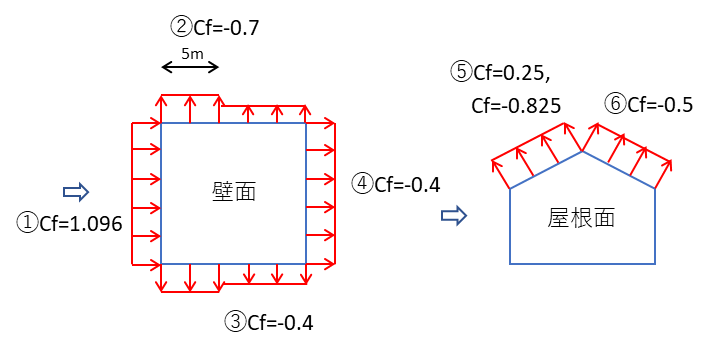
①風上壁面
\(Cf_{1}=0.896-(-0.2)=1.096\)
②側壁面 風上端部より0.5aの領域
\(Cf_{2}=-0.7-0=-0.7\)
③側壁面 風上端部より0.5aの領域以外の領域
\(Cf_{3}=-0.4-0=-0.4\)
④風下壁面
\(Cf_{4}=-0.4-0=-0.4\)
⑤風上屋根(その1 正の係数の場合)
\(Cf_{51}=0.05-(-0.2)=0.25\)
⑤風上屋根(その2 負の係数の場合)
\(Cf_{52}=-0.825-0=-0.825\)
⑥風下屋根
\(Cf_{6}=-0.5-0=-0.5\)
桁行方向の風力係数
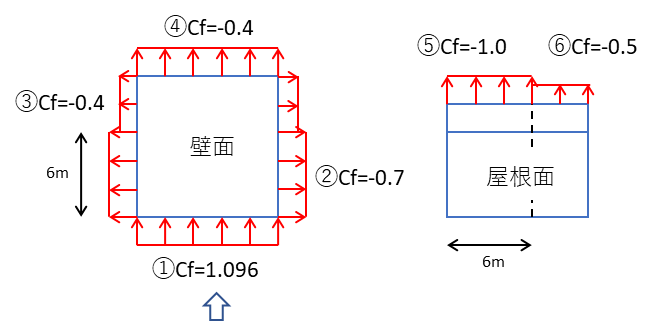
①風上壁面
\(Cf_{1}=0.896-(-0.2)=1.096\)
②側壁面 風上端部より0.5aの領域
\(Cf_{2}=-0.7-0=-0.7\)
③側壁面 風上端部より0.5aの領域以外の領域
\(Cf_{3}=-0.4-0=-0.4\)
④風下壁面
\(Cf_{4}=-0.4-0=-0.4\)
⑤風上屋根
\(Cf_{5}=-1.0-0=-1.0\)
⑥風下屋根 風上端部より0.5aの領域以外の領域
\(Cf_{6}=-0.5-0=-0.5\)
2.地表面粗度区分からErとGfを求める
つぎに地表面粗度区分からErとGfを求めます
平均風速の高さ方向の分布を表す係数 Er

地表面粗度区分をⅢ、建築物高さH=6mとした場合
\(H=6>Zb=5\)なので適用する式は
\(Er=1.7\left(\dfrac{H}{Z_{G}}\right)^\alpha\)
\(Er=1.7\left(\dfrac{6}{450}\right)^{0.20}\)
\(Er=0.72\)
ガスト影響係数 Gf

地表面粗度区分をⅢ、建築物高さH=6mとした場合
\(H=6<10\)なので
\(Gf=2.5\)
3.ErとGfからEと速度圧を求める
つぎに国土交通大臣が定めるEと速度圧qを求めます。
国土交通大臣が定めるE
平均風速の高さ方向の分布を表す係数とガスト影響係数が求まったので、
\(E=E_{r}^2 \cdot G_{f}=0.72^2\cdot2.5\)
\(E=1.30\)
速度圧q
場所が東京23区内ということは基準風速が34m/sになるので、速度圧は
\(q=0.6EV_{0}^2=0.6\cdot 1.30\cdot 34^2\)
\(q≒902N/m^2\)
\(q≒0.902kN/m^2\)
4.受風面積と速度圧から風荷重を求める
最後に風荷重を求めます。先ほど求めた風力係数と速度圧そして受風面積を掛合われば、風荷重は求めることができます。これもまた張間方向と桁行方向で異なります。
張間方向の風荷重
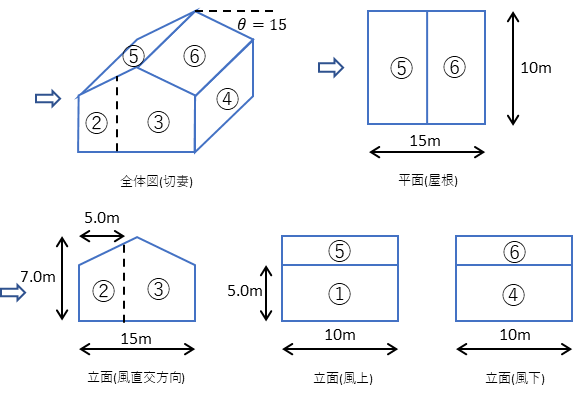
①風上壁面
\(W_{1}=1.096\cdot 0.902\cdot 50=49.43kN\)
②側壁面 風上端部より0.5aの領域 (両直交壁方向)
\(W_{2}=0.7\cdot 0.902\cdot 30=±18.94kN\)
③側壁面 風上端部より0.5aの領域以外の領域 (両直交壁方向)
\(W_{3}=0.4\cdot 0.902\cdot 60=±21.65kN\)
④風下壁面
\(W_{4}=-0.4\cdot 0.902\cdot 50=-18.04kN\)
⑤風上屋根(その1 正の係数の場合)
\(W_{51}=0.25\cdot 0.902\cdot 75/\cos{15}^{\circ}=17.51kN\)
⑤風上屋根(その2 負の係数の場合)
\(W_{52}=-0.825\cdot 0.902\cdot 75/\cos{15}^{\circ}=-57.78kN\)
⑥風下屋根
\(W_{6}=-0.5\cdot 0.902\cdot 75/\cos{15}^{\circ}=-35.02kN\)
桁行方向の風力係数
①風上壁面
\(W_{1}=1.096\cdot 0.902\cdot 90=88.97kN\)
②側壁面 風上端部より0.5aの領域(両直交壁方向)
\(W_{4}=-0.7\cdot 0.902\cdot 30=±18.94kN\)
③側壁面 風上端部より0.5aの領域以外の領域(両直交壁方向)
\(W_{3}=-0.4\cdot 0.902\cdot 20=±7.22kN\)
④風下壁面
\(W_{4}=-0.4\cdot 0.902\cdot 90=-32.47kN\)
⑤風上屋根
\(W_{5}=-1.0\cdot 0.902\cdot 90/\cos{15}^{\circ}=-84.04kN\)
⑥風下屋根 風上端部より0.5aの領域以外の領域
\(W_{6}=-0.5\cdot 0.902\cdot 60/\cos{15}^{\circ}=-28.01kN\)
引用元:建築物荷重指針・同解説
お知らせ
風圧力の算定シートを作成しました。
有料にはなりますが、皆様の設計の一助となれば幸いです。ぜひダウンロードしてください!!

まとめ
今回は風荷重についてまとめてきました。風荷重はとても複雑です算定するのに膨大な計算式が必要です。
風荷重は求めるものが多く、難しいのでもしも忘れてしまった場合はこちらの記事を参考にしてみてください!!
- 風荷重=(風圧力)×(風力係数)×(受風面積)
- 風圧力=0.6×(E)×(基準風速)


コメント