今回は前回に引き続き、独立上屋・ラチス構造の風力係数ついてわかりやすく解説していきたいと思います。
風力係数は建築の構造設計を行う上で必要となる風荷重を求める際に使う値です。風力係数は風荷重を扱う上で重要なキーワードなので、ぜひこの記事を参考にしてみて下さい!!

風力係数ってなんだ??
風力係数とは

風力係数とは建物形状ないしは風の向き、あるいは部材の形状によって変化する風荷重の大きさを係数で表した値です。
例えば同じ風でも風上と風下を比較すると風が先にあたる風上の方が大きく風下は小さくなることがイメージできるかと思います。
したがって同じ速度圧(風速)であっても建物形状や風の当たる場所によって建物に与える荷重の大きさ変化すると覚えておいてください。
風力係数の記号は[Cf]で表し、単位は無次元です。
建物の形式が閉鎖型と開放型の場合の風力係数についてはこちら記事を参考にしてみて下さい
風力係数(閉鎖型・開放型)とは
kzの求め方
kzは風力係数の算定に必要な値です。地表面粗度区分から求めることができ、kzの算定式は
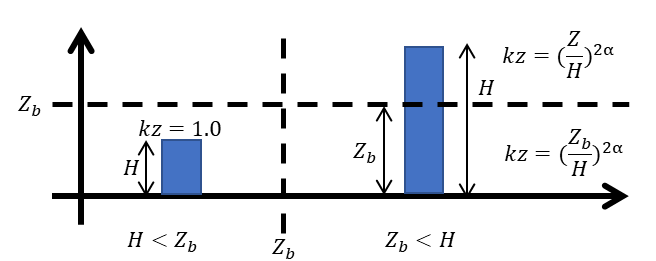
H≦Zbの場合
\(kz=1.0\)
H>ZbかつZ≦Zbの場合
\(kz=\left(\dfrac{Z_{b}}{H}\right)^{2\alpha}\)
H>ZbかつZ>Zbの場合
\(kz=\left(\dfrac{Z}{H}\right)^{2\alpha}\)
H:建築高さおよび軒高さの平均
Z:当該部分の地盤面からの高さ
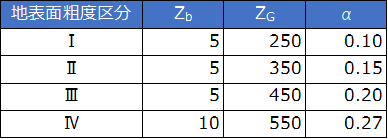
Zb,α:地表面粗度区分から求まる数値(下表を参照)
計算例として地表面粗度区分をⅡ、建築物高さH=20m Z=18mとした場合
\(H>Zb\) かつ \(Z>Zb\)なので適用する式は
\(kz=\left(\dfrac{Z}{H}\right)^{2\alpha}\)
\(kz=\left(\dfrac{18}{20}\right)^{2\cdot 0.15}\)
\(kz=0.969\)
地表面粗度区分についてはこちらの記事を参考にしてみて下さい
独立上屋の風力係数
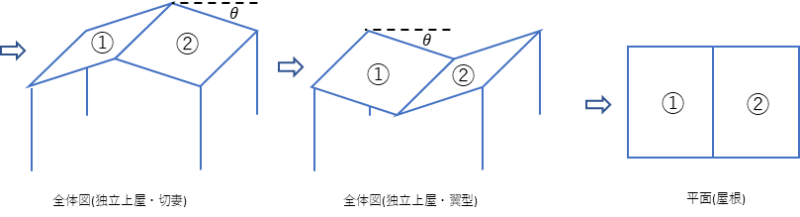
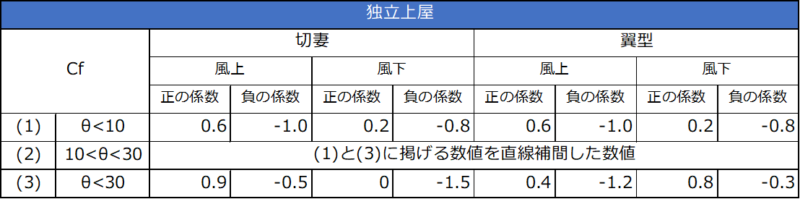
θ:屋根面が水平面となす角度(度)
※陸屋根の場合と同じ外圧係数の値を示します。
陸屋根の風力係数はこちらからどうぞ 風力係数(閉鎖型・開放型)とは
ラチス構造物
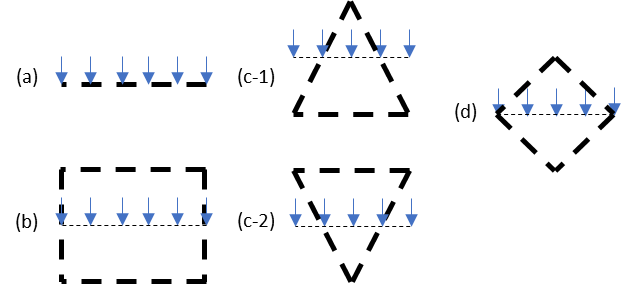
黒の太い破線がラチス材を表し、黒の細い破線が見付面積の最外縁までの距離を表しています。
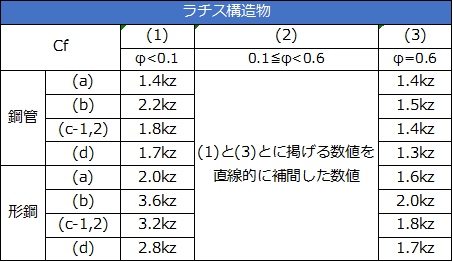
φ:充実率(風を受ける部分の最外縁により囲まれる面積に対する見付面積の割合)
充実率の算定は受圧する最外郭面積に対する見付面積として求められるが、ここで見付面積としては風上側の構成面のみの構成部材の面積を合計したものでよいです。風上側の鋼面での構成部材の隙間を通して見える風下側の構面を構成する部材の面積は見付面積に算入する必要はありません。
充実率が0.6を超える場合は風洞実験で風力係数を求めることが必要になります。
金網その他の網状の構造物
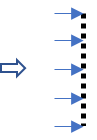

煙突のその他の円筒形の構造物
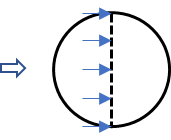
B:風向に対する見付幅(m)
H:建築高さおよび軒高さの平均

ラチス構造の風力係数の計算例

ここでラチス構造の風力係数の具体的な計算例を示します。
- ラチス構造 形状は(a)
- 地表面粗度区分Ⅱ
- 建築物の高さH=6m
- 風力係数を求めたい部分は地盤面からの高さZ=4mとする
- 部材はすべて形鋼L-65x65x6とする
1.kzを求める
まずラチス構造の風力係数の算出にはkzが必要になるので、地表面粗度区分Ⅱから

\(H>Zb\) かつ \(Z<Zb\)なので適用する式は
\(kz=\left(\dfrac{Zb}{H}\right)^{2\alpha}\)
\(kz=\left(\dfrac{5}{6}\right)^{2\cdot 0.15}\)
\(kz=0.95\)
2.充実率を求める
つぎにラチス構造の充実率を求めていきます。

ラチス構造は一定の間隔で同じような架構形状していることがほとんどです。であるならば、充実率は一定の間隔で計測した場合も同じなので簡易的に求めます。
[最外縁面積]
\(A=1000\times 500=50\cdot 10^4\)
[見付面積]
柱:\(1000\times 65\times 2=13\cdot 10^4\)
梁:\((500-65\cdot 2)\cdot 65=2.4\cdot 10^4\)
斜材:\((500-65\cdot 2)\cdot\sqrt{2}\cdot 65=3.4\cdot 10^4\)
見付面積の合計は
\((13+2.4+3.4)\cdot 10^4=18.8\cdot10^4\)
したがって充実率φは(見付面積/最外縁面積)なので
\(\phi=18.8/50=0.376\)
3.風力係数を求める
最後に風力係数を求めます。ラチス構造の(a)かつ形鋼、充実率は0.376なので線形補間してきます。

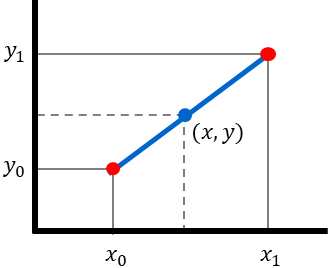
求めたい風力係数をy=Cf,充実率をx=φとすると
\(y=y_{0}+(y_{1}-y_{0})\dfrac{x-x_{0}}{x_{1}-x_{0}}\)
\(y=2.0kz+(1.6kz-2.0kz)\dfrac{0.376-0.1}{0.6-0.1}\)
\(y=1.78\)
\(Cf=1.78kz=1.78\cdot0.95=1.69\)
このようにラチス材の風力係数を求めることができます。
引用元:建築物荷重指針・同解説
まとめ
今回は風力係数についてまとめてきました。風力係数は風荷重を算定するのに必要な知識です。
風力係数は求めるものが多く、難しいのでもしも忘れてしまった場合はこちらの記事を参考にしてみてください!!
- ラチス構造の充実率をもとめる
- 直線補間の式を覚えておこう


コメント
独立上屋の風力係数の表ですが、
(1)の①風上の歩の係数ですが、
-0.1ではなく、-1.0ではありませんか?
コメントありがとうございます。
おっしゃる通りでございます。記事を修正させていただきました。
今後ともよろしくお願いいたします。