今回は2020年度一級建築士 学科試験Ⅳ構造のNo.2の問題についてまとめていきたいと思います
今回は構造力学のたわみ及び力のつり合い式から出題されています
3次元的な単純梁の問題で初めて見る人も多いとおもいます。この記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

3次元の単純梁は見たことない!!どうやって解くの!?
問題 No.2
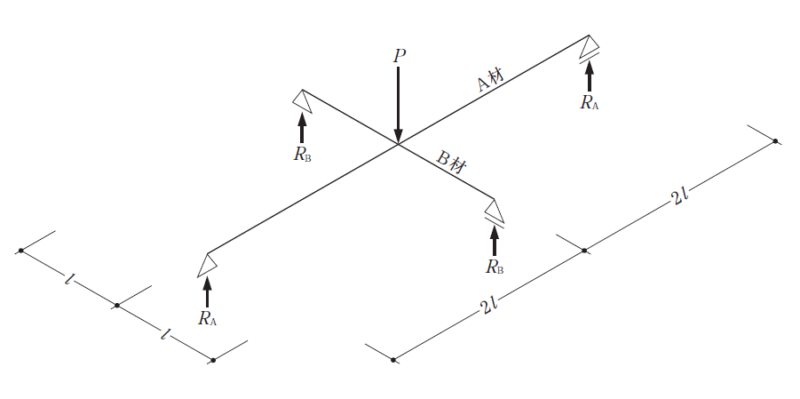
[No.2]
図に示す交差梁のA材とB材の交点に集中荷重P が作用したときのA材、B材の支点の反力をそれぞれRA、RBとするとき、その比として、正しいものは、次のうちどれか。なお、A材とB材は等質等断面とし、梁の重量は無視するものとする。
[選択肢](RA:RB)
- 1:1
- 1:2
- 1:4
- 1:8
この問題キーワードは
- 単純梁の力のつり合い式
- 単純梁のたわみ
前提条件
この問題は以下の知識について問われています
- 力のつり合い式による反力の求め方
- たわみ公式
ひとつずつ紐解いていきましょう!!
力のつり合い
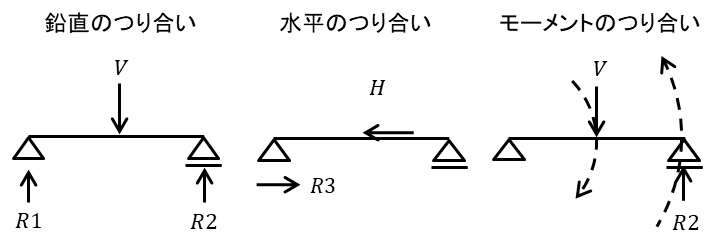
力がつり合う(静止や等速直線運動のような)状態は荷重=反力になる、つまり力の合計は0であることです
力のつり合い式は基本的には2軸つまり鉛直方向と水平方向で考えます。数式で表すならば
鉛直方向:\(\Sigma V=0\)
水平方向:\(\Sigma H=0\)
モーメント:\(\Sigma M=0\)
V:鉛直方向の力
H:水平方向の力
M:ある基点周りのモーメント
単純梁の集中荷重のたわみ
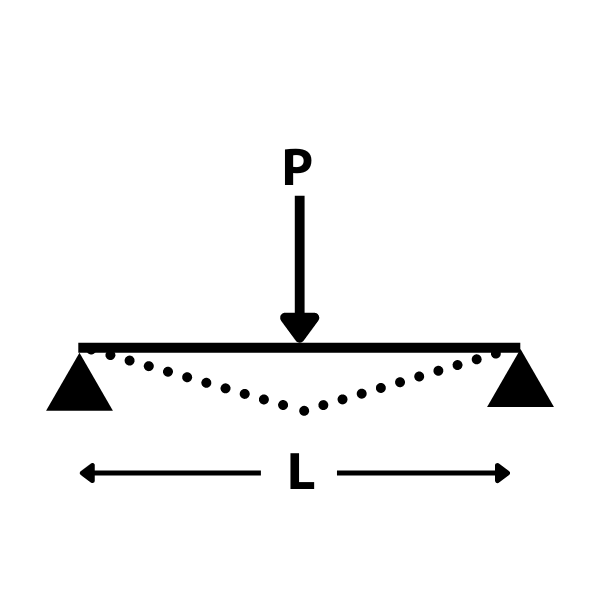
単純梁・集中荷重のたわみの公式は
\(\delta=\dfrac{PL^3}{48EI}\)
δ:たわみ(梁中央)
P:集中荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
たわみの導出や覚え方について詳しくはこちらをご覧ください
解き方
解く順序は
- 力のつり合い式をたてる
- 梁のたわみを求める
- 反力を求める
ひとつずつ算出していきましょう
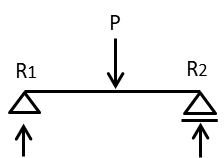
まずは一番簡単な鉛直方向の力のつり合いを求めます。式をたてると
\(\Sigma V=0\)
\(P=2R_{A}+2R_{B}\)
ここで多くの人がモーメントのつり合い式をたてて解こうとしてしまいますが、計算していくと解けないことがわかると思います。そこで中央でのたわみが縦と横のモデルで一致することに注目します。
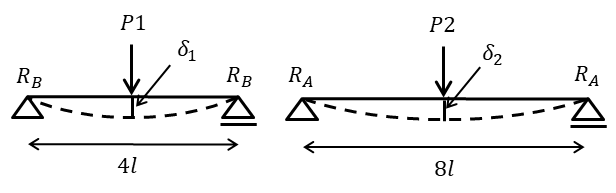
モデルを2つに分けて考えると解きやすいと思います。わけたモデルは上図のようになり数式で表現すると、
\(\delta_{1}=\delta_{2}\)
両方のたわみは一致し、
\(P=P_{1}+P_{2}\)
両方の荷重の合計は元の荷重は一致します。
そして単純梁-集中荷重のたわみの公式は
\(\delta=\dfrac{PL^3}{48EI}\)
モデルに合わせて\(L \Rightarrow 4l \quad L \Rightarrow 8l \)に変換します
\(\delta_{1}=\dfrac{8P_{1}l^3}{3EI}\)
\(\delta_{2}=\dfrac{32P_{2}l^3}{3EI}\)
たわみは一致することから等式が成り立つので結果
\(P_{1}=8P_{2}\)となり
\(P_{1}:P_{2}=8:1\)であることがわかりました。
最後にそれぞれのモデルの荷重から反力を計算します。すでに荷重比によって反力比も決定していますが、計算で示すと鉛直のつり合いより
\(P_{1}=2R_{B}\)
\(R_{B}=P_{1}/2\)
\(P_{2}=2R_{A}\)
\(R_{A}=P_{2}/2\)
つまりは
\(R_{A}:R_{B}=\dfrac{P_{2}}{2}:\dfrac{P_{1}}{2}=P_{2}:8P_{2}\)
\(R_{A}:R_{B}=1:8\)
最終的な答えは④でした
まとめ
今回は2020年 一級建築士 学科試験Ⅳ構造 No.2の解説をしてきました
今回のポイントは単純梁のたわみと気が付けたかどうかです。
公式をすぐに忘れてしまう人も多いかと思いますが、今回の問題は単純梁のたわみの公式の分母の係数48については必要ありません。係数がわからなくとも問題は解けます。解くために必要なのは\(L^3\)の部分です。ここだけでもよく覚えておいてください!!
過去のたわみ記事ではたわみの公式を導出できる方法を紹介していますので、是非たわみの記事もあわせて是非参考にしてみて下さい!!


コメント