今回は2021年度一級建築士 学科試験Ⅳ構造のNo.2の問題についてまとめていきたいと思います
今回は構造力学のたわみ及び力のつり合い式から出題されています
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
問題 No.2
[No.2]
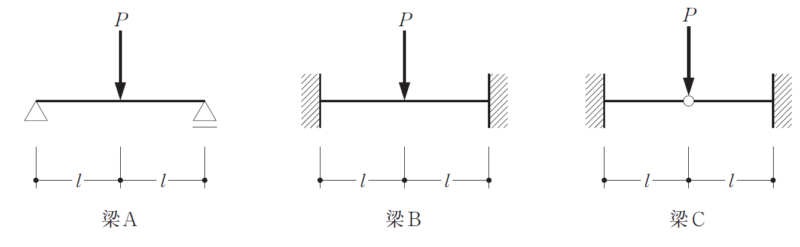
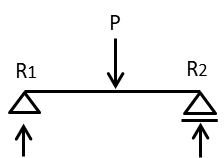
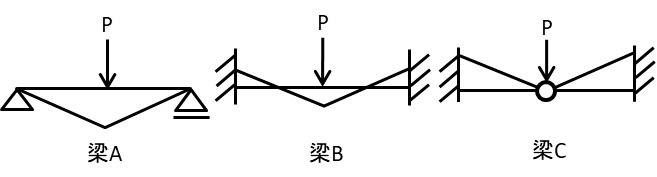
図のような梁A、梁B及び梁Cにそれぞれ荷重P が作用している場合、梁A、梁B及び梁Cにおける応力、たわみ等の大きさの比(梁A:梁B:梁C)として、最も不適当なものは、次のうちどれか。ただし、全ての梁は同一断面で、全長にわたって等質等断面の弾性部材とし、自重は無視する。
[選択肢](左から梁A:梁B:梁Cの比率とする)
・鉛直方向の支点反力 1:1:1
・最大曲げモーメント 2:1:2
・最大せん断力 1:1:1
・荷重点のたわみ 2:1:2
この問題キーワードは
- 単純梁と固定梁の曲げモーメント
- 梁Cのたわみ
前提条件
この問題は
・力のつり合い式による各支点の反力
・せん断のQ図
・モーメントのM図
・たわみ公式
についての知識が問われています
力のつり合い
力がつり合う(静止や等速直線運動のような)状態は荷重=反力になる、つまり力の合計は0であることです
力のつり合い式は基本的には2軸つまり鉛直方向と水平方向で考えます
数式で表すならば
鉛直方向:\(\Sigma V=0\)
水平方向:\(\Sigma H=0\)
V:鉛直方向の力
H:水平方向の力
単純梁の集中荷重のたわみ
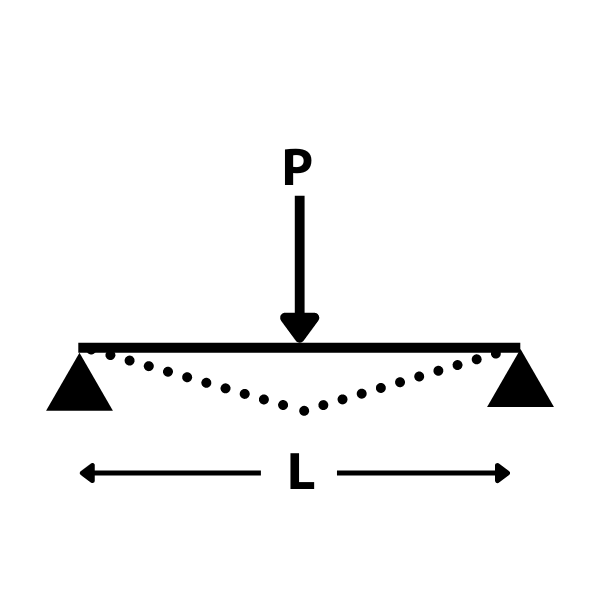
単純梁・集中荷重のたわみの公式は
\(\delta=\dfrac{PL^3}{48EI}\)
δ:たわみ(梁中央)
P:集中荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
たわみの導出や覚え方について詳しくはこちらをご覧ください
両端固定梁の集中荷重のたわみ
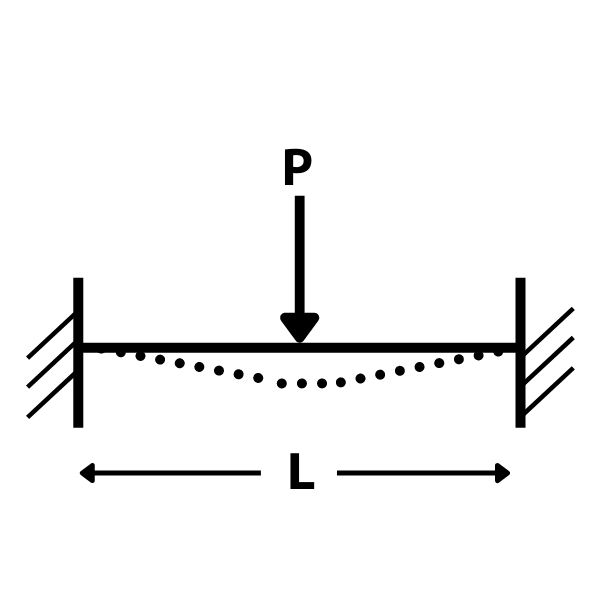
両端固定梁・集中荷重のたわみの公式は
\(\delta=\dfrac{PL^3}{192EI}\)
δ:たわみ(梁中央)
P:集中荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
両端固定梁のたわみの導出や覚え方について詳しくはこちらをご覧ください
片持梁の集中荷重のたわみ
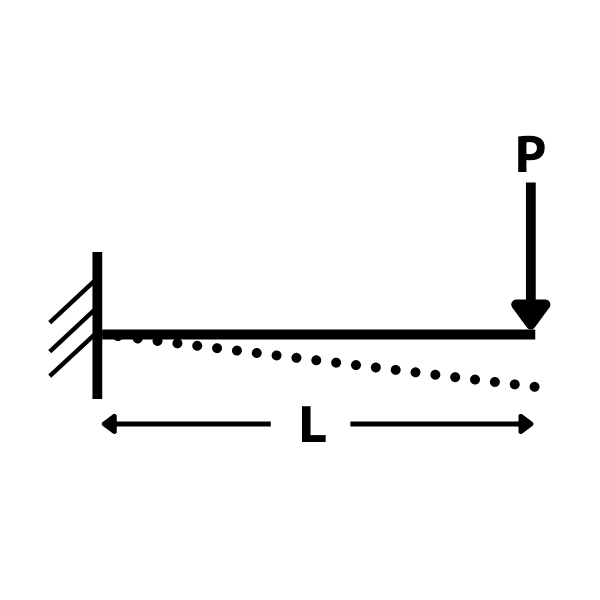
片持梁・集中荷重のたわみの公式は
\(\delta=\dfrac{PL^3}{3EI}\)
δ:たわみ(梁中央)
P:集中荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
片持梁のたわみの導出や覚え方について詳しくはこちらをご覧ください
解き方
解く順序は
- 力のつり合い式より鉛直方向反力の算出
- 最大モーメントと最大せん断力の算出
- 各モデルのたわみの算出
ひとつずつ算出していきましょう
まずは一番簡単な鉛直方向の反力の算出です。この問題は共通して対称軸をもつモデルなので左右の反力が同じです。(もし荷重Pの位置が中心からずれていましたら簡単には解けません!)
すべてのモデルで同じなので左の反力をR1・右の反力をR2とし、式をたてると
\(\Sigma V=0\)
\(P=R_{1}+R_{2}\)
\(R_{1}=R_{2}\) から
\(R_{1}=R_{2}=\dfrac{P}{2}\)
したがって鉛直方向の反力の比は『1:1:1』です
※この問題自体が鉛直方向の支点反力の比ではなく、鉛直方向の合計反力の比や右側支点反力の比のように指定しなければならなく、もし荷重Pの位置が中心からずれたときになにを比較するかわからなくなるため問題の定義不足と言えます。
つぎに最大曲げモーメントを求めます。最大曲げモーメントを求めるためはM図を描きます。最大曲げモーメントはM図から絶対値の最大箇所を見つけるので梁Bだけ注意が必要です
梁Cは普段から見慣れないモデルですが片持梁が2つあるものとして考えて問題ないです
梁Aの中央曲げモーメントは
\(M=\dfrac{Pl}{2}\)
梁Bの中央曲げモーメントは
\(M=\dfrac{Pl}{4}\)
梁Bの端部曲げモーメントは
\(M=\dfrac{Pl}{4}\)
したがって梁Bの最大曲げモーメントは
\(M=\dfrac{Pl}{4}\)
梁Cの端部曲げモーメントは
\(M=\dfrac{Pl}{2}\)
したがって最大曲げモーメントの比は『2:1:2』です
つぎに最大せん断力を求めます。最大せん断力を求めるためはQ図を描きます。せん断力は反力から求めることができるので先ほど解いた鉛直支点反力の比と同じになります。
梁A・梁B・梁Cの支点反力はいずれも\(P/2\)なので
梁A・梁B・梁Cの最大せん断もいずれも\(P/2\)になります
したがって最大せん断力の比は『1:1:1』です

最後にたわみを比較します。単純梁と両端固定梁の集中荷重によるたわみは公式より
単純梁‐集中荷重によるたわみは
\(\delta=\dfrac{Pl^3}{48EI}\)
\(l\Rightarrow 2l\) に変更する必要があるので今回の場合のたわみは
\(\delta=\dfrac{Pl^3}{6EI}\)
両端固定梁‐集中荷重によるたわみは
\(\delta=\dfrac{Pl^3}{192EI}\)
\(l\Rightarrow 2l\) に変更する必要があるので今回の場合のたわみは
\(\delta=\dfrac{Pl^3}{24EI}\)
最後の梁Cのモデルに関してはモデルを2等分し片持梁モデルのたわみにして考えると簡単に解けます
片持ち梁‐集中荷重によるたわみは
\(\delta=\dfrac{Pl^3}{3EI}\)
荷重についてはモデルを2等分したならば反力がP/2とつり合うように
\(P\Rightarrow P/2\) に変更する必要があるので今回の場合のたわみは
\(\delta=\dfrac{Pl^3}{6EI}\)
以上をまとめると
\(\dfrac{Pl^3}{6EI}:\dfrac{Pl^3}{24EI}:\dfrac{Pl^3}{6EI}\)
したがってたわみの比は『4:1:4』です
最終的な答えは④でした
まとめ
今回は2021年 一級建築士 学科試験Ⅳ構造 No.2の解説をしてきました
今回のポイントは梁Bの最大曲げモーメントを算出できたか、あるいは梁Cを片持ち梁として解くことができたかどうかです。
公式をすぐに忘れてしまう人も多いかと思いますが過去のたわみ記事ではもし忘れてしまってもたわみの公式を導出できる方法を紹介していますので、是非たわみの記事もあわせて参考にしてみて下さい
・荷重が等分布荷重になった場合
・荷重点が中央部でない場合
・たわみ角について問われる場合
こちらも自分で問題を作って解いてみるとよいでしょう!!




コメント