今回は2021年度二級建築士 学科試験Ⅲ建築構造のNo.5の問題についてまとめていきたいと思います
今回は構造力学の静定ラーメンの曲げモーメントの問題から出題されています
力学の基本的な問題なのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
問題 No.5
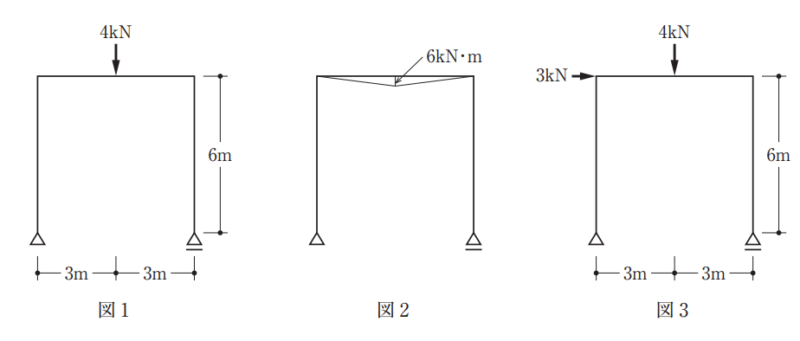
[No.5]
図 1 は鉛直方向に外力を受ける静定ラーメンであり、その曲げモーメント図は図 2 のように表せる。図 1 の静定ラーメンに水平方向の外力が加わった図 3 の静定ラーメンの曲げモーメント図として、正しいものは、次のうちどれか。ただし、曲げモーメント図は、材の引張側に描くものとする。
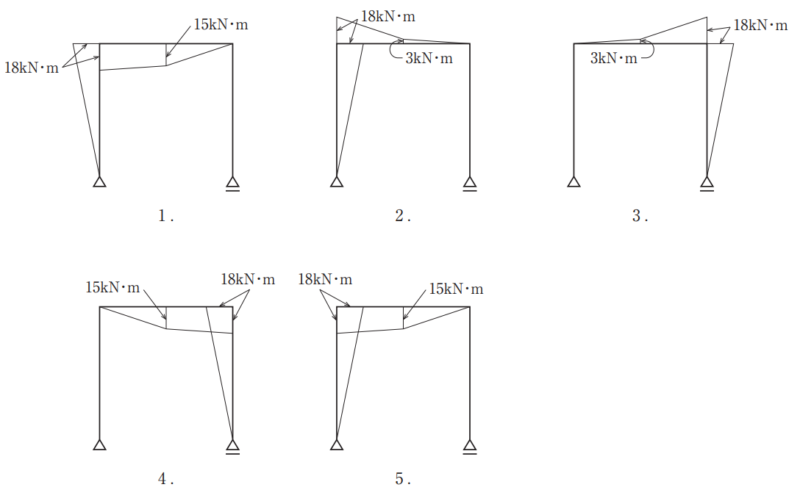
[選択肢]
この問題を解くためのキーワードは
- 静定架構の曲げモーメント
- 剛節点の応力伝達
だと思います。力学の基本的な知識が問われています。
前提条件
この問題を解くためには曲げモーメントのM図について覚えておく必要があります。
M図とは
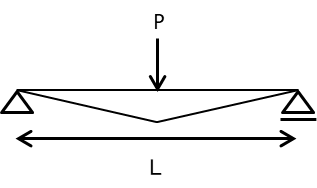
M図とは、部材に生じる曲げモーメントの値を図示したものです。上図では荷重点で最も大きい曲げモーメントが発生しているのがわかります。
このように図にすることで、体系的に曲げモーメントの大小を把握できます。
曲げモーメント図の描き方は
- 支点反力を求める
- 支点から\(x\)進んだ点での\(M(x)\)の式をたてる
- \(M(x)\)のグラフを描く
曲げモーメント図の描くルールとして
- 引張側にモーメントを描く(日本での暗黙のルール、海外などでは圧縮側に描くこともある)
- ピン支点、ローラー支点ではモーメントは0
剛節点の応力伝達

静定ラーメンの問題で剛節点の応力伝達は一般的な単純梁をイメージするとわかりやすいです。
伝達されるモーメントは両端で大きさ等しく、向きも折り曲げたようにつり合います。
解き方
解く方法順序は
- 支点反力を求める
- 右柱のせん断力を求める
- 左柱の引張側にモーメントを描く
- 中央でモーメントのつり合い式を求める
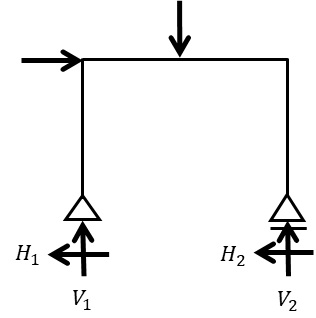
ひとつずつ算出していきましょう
まずは与えられた荷重をもとに支点反力を求めます。左の支点を\(V_{1},H_{1}\)右の支点を\(V_{2},H_{2}\)とします。
水平成分:\(H_{1}=3kN \quad H_{2}=0kN \) …(1)式
鉛直成分:\(V_{1}+V_{2}=4kN\) …(2)式
モーメントのつり合い式を左の支点を基点にすると
\(3\cdot6+4\cdot3-V_{2}\cdot6=0\)
(2)式より
\(V_{2}=5\)
\(V_{1}=-1\)
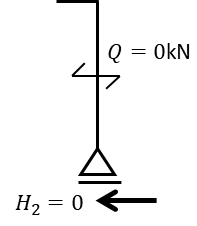
つぎに右柱のせん断力を求めます。とは言っても先ほど右の支点がローラー支点のため(1)式より
\(H_{2}=0kN \)
したがって右柱のせん断力は0つまりは右柱のモーメントが0になります。
この時点で選択肢の3・4は不正解となります。(残りは1・2・5)
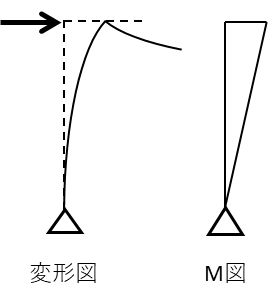
つぎに左柱の引張側にモーメントを描きます。
柱の変形図を想像し引張側にM図を描くため、柱の右側に引張が生じることがわかります。もしわからない場合は片持梁の集中荷重のM図を描いてください。詳しい解説はこちら→片持梁・集中荷重のたわみ
この時点で柱の左側にモーメントがある選択肢の1は不正解となります。(残りは2・5)

最後に2・5の違いは剛節点の伝達モーメントと中央の曲げモーメントが異なるので剛節点の応力伝達でも解くことができますが、中央の曲げモーメントを計算します。
\(M=V_{1}\cdot 3+H_{1}\cdot 6\)
\(M=-1\cdot 3+3\cdot 6=15\)
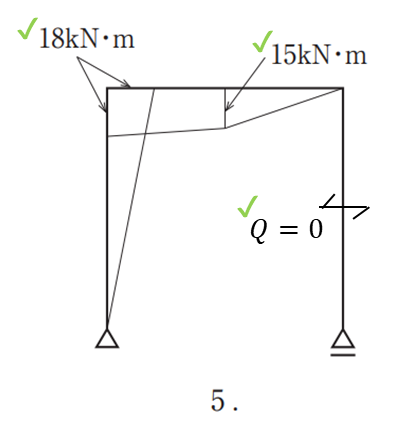
したがって答えは⑤でした
まとめ
今回は2021年 二級建築士 学科試験Ⅲ建築構造 No.5の解説をしてきました。
今回の問題は静定ラーメンの問題でM図を求める問題でした力学の中では基本中の基本であるので、もし忘れてしまった方は是非とも解けるようにしてください!!
・曲げモーメント荷重の場合
・たわみを求める場合
こちらも自分で問題を作って解いてみるとよいでしょう!!




コメント