今回は2022年度一級建築士 学科試験Ⅳ構造のNo.4の問題についてまとめていきたいと思います。
今回は崩壊荷重の問題から出題されています。
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

崩壊荷重ってなんだ?
問題 No.4
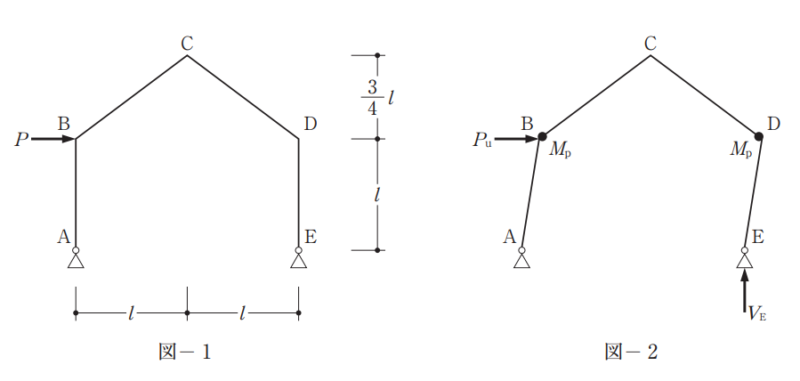
図-1 のような水平荷重Pを受ける山形ラーメンにおいて、Pを増大させたとき、その山形ラーメンは、図-2 のような梁端部に塑性ヒンジを生じる崩壊機構を示した。山形ラーメンの崩壊荷重がPuであるとき、最も不適当なものは、次のうちどれか。ただし、梁の全塑性モーメントはMpとする。
[選択肢]
- 水平荷重Puは \(\dfrac{2Mp}{l}\)である。
- 柱ABの軸力は \(\dfrac{Mp}{l}\) の引張力である。
- C点の曲げモーメントは0である。
- E点の鉛直反力VEは \(\dfrac{Mp}{l}\) である。
この問題キーワードは
- 崩壊荷重の求め方
- 力のつり合いの求め方
の2点ですここだけ押さえておけばこの問題は簡単です。
崩壊荷重の求め方
一級建築士試験の問題でよく出題される崩壊荷重の求め方は仮想仕事の原理に基づきます。仮想仕事の原理とは簡単に言えば外力と内力のつり合った状態を指します。
式で表すと
仮想仕事の原理
\(Σ(Pu×\delta)=Σ(Mp×\theta)\)
Pu:崩壊荷重
δ:変位量あるいは変形量
Mp:全塑性モーメント
θ:たわみ角
崩壊荷重の求める手順は以下の通りです。
- 崩壊荷重時の変形量・たわみ角を仮定する
- 外力(荷重)の仕事量ΣP×δの式をつくる
- 内力(部材耐力)の仕事量ΣM×θの式をつくる
- 仮想仕事の原理の等式(ΣP×δ=ΣM×θ)から導く
詳しい解説はこちらの記事を参考にしてみて下さい
解き方
今回の問題の解く順序は先ほど紹介したように
- 崩壊荷重時の変形量・たわみ角を仮定する
- 外力(荷重)の仕事量ΣP×δの式をつくる
- 内力(部材耐力)の仕事量ΣM×θの式をつくる
- 仮想仕事の原理の等式ΣP×δ=ΣM×θから導く
まずは変形量とたわみ角を仮定します。
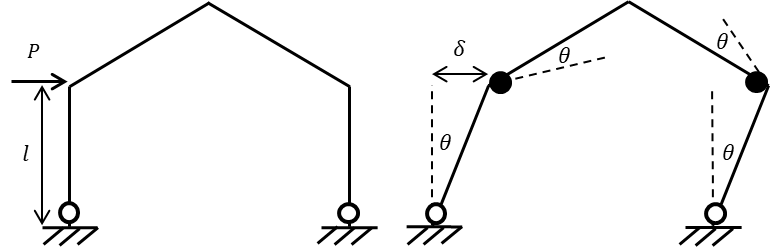
ある一定の変形量δ 進んだと仮定し、その時のヒンジの角度をθとします。各節点は元の角度から変形が進むので破線のような
左右の柱のたわみ角をθとします。
柱頭の変位量が同じになるので
\(\delta=sin\theta\cdot l\) とおきます。
ただしたわみ角θが微小であることに限ればsinθ≒θとなるので
\(\delta=\theta\cdot l\) …(1)
となります。
2つ目に外力の仕事量の式を作ります。外力の仕事量Woは荷重×変位で表されます。したがって
\(\Sigma Wo=Pu\cdot\delta\) …(2)
3つ目に内力の仕事量の式を作ります。内力とは部材自身の持つエネルギーのようなもので内力の仕事量は全塑性モーメント×部材のたわみ角で表されます。
たわみ角はヒンジのあるところに存在します。梁のたわみ角は元の角度を保ちながら変形を想像しながら描きます。(柱脚のピンはもともと回転しているので仕事量を考慮しません)内力を式で表すと
\(\Sigma Wi=Mp\cdot\theta+Mp\cdot\theta=2Mp\cdot\theta\) …(3)
最後に(2),(3)式を等式にまとめ、仮想仕事の原理の等式から導くと
\(\Sigma Wo=Pu\cdot\delta\)
\(\Sigma Wi=2Mp\cdot\theta\)
\(Pu\cdot\delta=2Mp\cdot\theta\)
さらに(1)式\(\delta=\theta\cdot l\)を代入することで
\(Pu\cdot\theta\cdot l=2Mp\cdot\theta\)
崩壊荷重Puの式としてあらわすと、
\(Pu=\dfrac{2Mp}{l}\)
したがって①は正しいことがわかりました。
これでやっと一つの選択肢が解けましたがあとの選択肢は力のつり合いで求めることができます。
④の検証はPuがわかったことから点Aまわりの力のつり合いを考えると
\(\Sigma M_{A}=0\)
\(\Sigma M_{A}=Pu\cdot l -V_{E}\cdot 2l\)
\(\Sigma M_{A}=\dfrac{2Mp}{l}\cdot l-V_{E}\cdot 2l\)
\(V_{E}=\dfrac{Mp}{l}\)
したがって④も正しいことがわかりました。
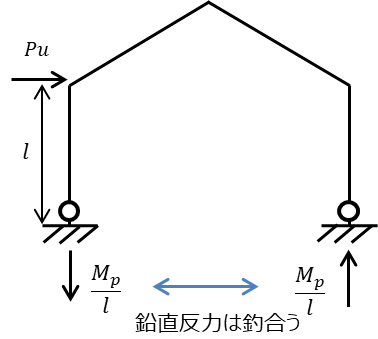
同じ考え方で②も対称で同じになるので、
柱DEには圧縮力\(\frac{Mp}{l}\)に釣合うように柱ABには引張力\(\frac{Mp}{l}\)が発生するので②も正しいことがわかりました。
消去法で③が不適当で答えになります。
消去法ではなくちゃんと解くには点Cまわりの力のつり合いを考えると
\(\Sigma M_{C}=Pu\cdot\dfrac{3}{4}l-V_{A}\cdot l+V_{E}\cdot l\)
柱の軸力から以下のことがわかります。
\(V_{A}=\frac{Mp}{l}=-V_{E}\)
したがって
\(\Sigma M_{C}=Pu\cdot\frac{3}{4}-2V_{A}\cdot l\)
\(\Sigma M_{C}=\dfrac{2Mp}{l}\cdot\dfrac{3}{4}l-2\dfrac{Mp}{l}\cdot l\)
\(\Sigma M_{C}=\dfrac{3}{2}Mp-2Mp=-Mp/2\)
Mc≠0でしたので③は不適当であります。
まとめ
今回は2022年 一級建築士 学科試験Ⅳ構造 No.4の解説をしてきました。
今回の問題のポイントは仮想仕事原理の計算のしかたです。一見難しそうに見えますが比較的簡単な計算方法の問題です。
崩壊荷重の問題は毎年のように出る頻出問題です。是非解けるのようになって下さい!!
対策
- 荷重数が増える場合
- 柱の長さが左右で違う場合
こちらも自分で問題を作って解いてみるとよいでしょう!!
こちらは過去の類似問題ですので参考にしてください。






コメント