今回は断面一次モーメントについてわかりやすく説明していきたいと思います
断面一次モーメントは断面二次モーメントと名前は似ているものの使う機会は少ないです
しかし断面一次モーメントはせん断応力度の計算などに必要になる重要なキーワードです
また断面の重心位置を探る手段として非常に有用なので是非参考にしてください!!
断面一次モーメントとは
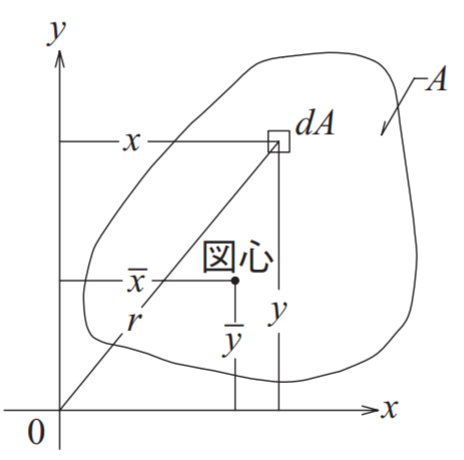
断面一次モーメントとは任意の軸から距離と微小面積dAの掛け合わせの合計値になります。一般的には重心軸を求める際に使われるパラメーターです。
表記は[Sx],[Sy]あるいは[Gx],[Gy]で表すこともあります。単位は[cm3]で表記することが多いです
式で表すと
\(S_{x}=\int ydA\ ,\ S_{y}=\int xdA\)
Sx Sy :X軸,Y軸周りの断面一次モーメント
y :任意の軸x0からの距離
x :任意の軸y0からの距離
dA:微小面積要素
断面二次モーメントの公式が\( I_{x}=\int y^2dA\)でかなり似ていて覚えやすいです
(yの1乗は一次モーメント、yの2乗は二次モーメントと覚えましょう!)
しかしながら断面一次モーメント単体で使うことはめったにないですが
重心軸を求める際に一次モーメントの計算を経由して求めるため
以下の式がより重要になります
\(y_{0}=\dfrac{S_{x}}{A}\ ,\ x_{0}=\dfrac{S_{y}}{A}\)
Sx Sy :X軸,Y軸周りの断面一次モーメント
y0 :Y座標の重心軸
x0 :X座標の重心軸
A :断面積
断面一次モーメントの特徴は重心軸まわりの断面一次モーメントを求めるとS=0になります
断面一次モーメントの求め方
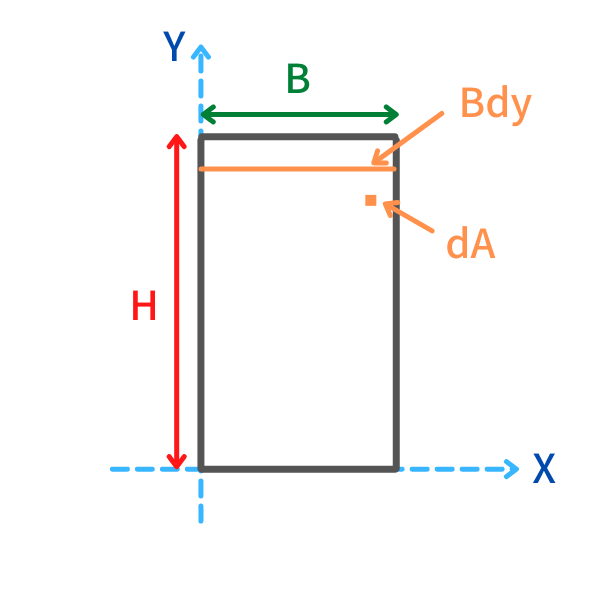
断面一次モーメントの求め方の例として長方形断面のx軸周りの断面一次モーメントを計算します
①まず最初は基準となる座標軸を設定します。断面の左下に原点が来ると求めやすいと思います
②次にdAの微小面積要素はB幅に並べると
\(dA=B×dy\) になります
③積分区間が[0,H]になるので公式をこのように変化させます
\(\displaystyle S_{x}=\int ydA = \int_{0}^{H}yBdy\)
④積分と解くと
\(\displaystyle S_{x}=B\left[ \frac{y^2}{2}\right]_{0}^{H}=\frac{BH^2}{2}\)
となり長方形の断面一次モーメントが簡単に求まりました!
もっと簡単な断面一次モーメントの求め方
断面一次モーメントを求めるのにわざわざ積分したいとは誰も思いません
より簡単な方法で表すと
断面一次モーメントは面積×断面の重心から軸までの距離で計算できます
\(S_{x}=A\times y_{o}\)
\(S_{y}=A\times x_{o}\)
Sx Sy :X軸,Y軸周りの断面一次モーメント
y0 :Y座標の重心軸
x0 :X座標の重心軸
A :断面積
先ほどの例で計算すると
①断面積を求める
\(A=B\times H\)
②原点(0,0)を左下におくとyo,xoを求める
yo,xoはHの半分、Bの半分になるので
\(\displaystyle y_{0}=\frac{H}{2},x_{0}=\frac{B}{2} \)
③Sx,Syを求める
\(Sx=Ay_{0}=\frac{BH^2}{2}\)
\(Sy=Ax_{0}=\frac{B^2H}{2}\)
で簡単に断面一次モーメントが求まりました!
重心の求め方
先ほども述べましたが断面一次モーメントだけを求めても構造的にほとんど意味を持ちません
では何のために使うかと言えば
見た目からだけでは重心位置を判断できない図形や断面の重心を求めるために使います
他にも断面補強、断面欠損したどんな断面でも重心を求めることができます
2019年の一級建築士試験の問題[No.1]は以下の図形の重心を求める問が出題されました
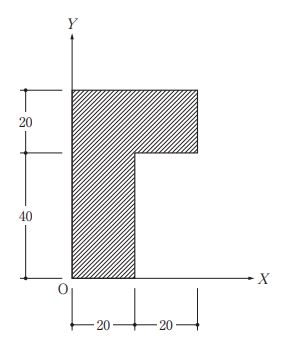
この見た目から瞬時に重心を見つけることはできないと思います
したがって\(\displaystyle y_{0}=\frac{S_{x}}{A} , x_{0}=\frac{S_{y}}{A}\) の公式から求めていきたいと思います
具体的な計算例を紹介します
このようなL字断面の場合は初めに2つの長方形に分けます
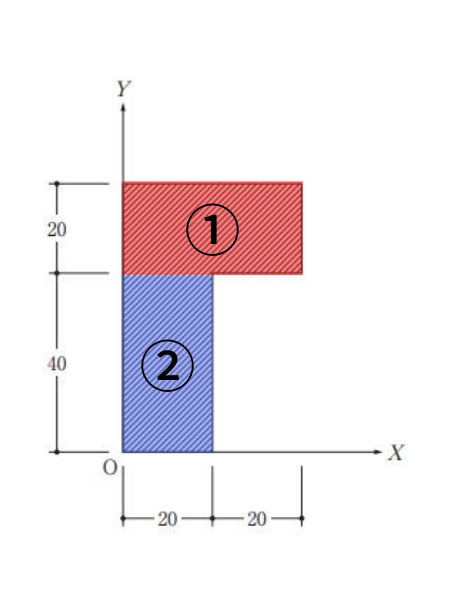
まずは面積を算出します
①\(A_{1}=40\times20=800\)
②\(A_{2}=20\times40=800\)
次にそれぞれ断面の重心を算出します
①\(y_{1}=40+20/2=50\)
\(x_{1}=40/2=20\)
②\(y_{2}=40/2=20\)
\(x_{2}=20/2=10\)
その次は断面一次モーメントを算出します
\(S_{x1}=A_{1}y_{1}=40000\)
\(S_{y1}=A_{1}x_{1}=16000\)
\(S_{x2}=A_{2}y_{2}=16000\)
\(S_{y2}=A_{2}x_{2}=8000\)
最後は合成した断面の重心位置を算出します
\(\displaystyle y_{0}=\frac{S_{x1}+ S_{x2}}{A_{1}+ A_{2}} =\frac{56000}{1600}=35\)
\(\displaystyle x_{0}=\frac{S_{y1}+ S_{y2}}{A_{1}+ A_{2}} =\frac{24000}{1600}=15\)
以上で見た目からはわからなかった重心位置を計算で求めることができました
これ以外の断面でも丸形や斜めの断面であっても
断面を分けて考えることでどんな複雑な形状も重心位置を求めることができます!!
まとめ
今回は断面一次モーメントについて説明してきました
断面一次モーメント自体の値はほとんど意味を持ちませんが
複雑な断面の重心を求めるために必要なパラメーターです
重心を求めたいと思った時はぜひこの記事を参考にしてみて下さい!!


コメント