今回は断面係数についてわかりやすく説明していきたいと思います
断面係数は曲げ応力を算出する際に必要となるパラメーターであり、一級建築士試験においてもよく出題される問題でもありますのでしっかりとした知識になるよう説明していきます
断面係数とは
断面係数(英:elastic section modulus)は断面による曲げに対する抵抗値と表現できます。断面係数が大きければ曲げ応力度は小さくなり、断面係数が小さければ曲げ応力度は大きくなるという特徴があります
もともとは断面二次モーメントから導出された値であり断面二次モーメントが求められなければ断面係数も求まりません
記号はZで表し、単位はcm3で表すことが多いです
式で表すと
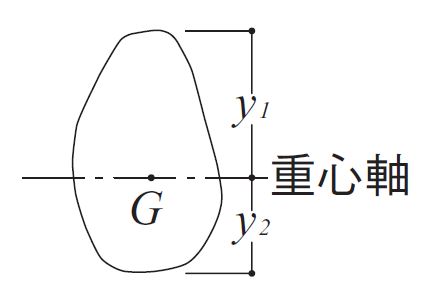
\( Z_{1}=\dfrac{I}{y_{1}} \ ,\ Z_{2}= \dfrac{I}{y_{2}} \)
Z1, Z2 : 断面係数
I : 断面一次モーメント
y1 ,y2 : 重心軸から断面の最外端までの距離
断面係数の特徴は重心軸からのyの距離が遠くなる方が断面係数が大きく有利になります
y1が大きくともy2が小さければ断面係数は小さくなってしまいます実務はほとんどの場合で\(min[Z_{1},Z_{2}]\)とするので片側に重心が寄っている断面よりも対称断面の方が効率良く断面力を使えているとも言えます
一般的な断面は重心軸に対して対称でy1=y2となるので断面係数は\(Z=I/y\)となります
また似たような値で塑性断面係数Zpがありますがまた意味が変わってくるので混同しないように注意して下さい
断面係数と曲げ応力度
断面係数は曲げ応力度を算出するために必要なパラメーターです
なぜ曲げ応力度と深く関係するか説明するために例を挙げます
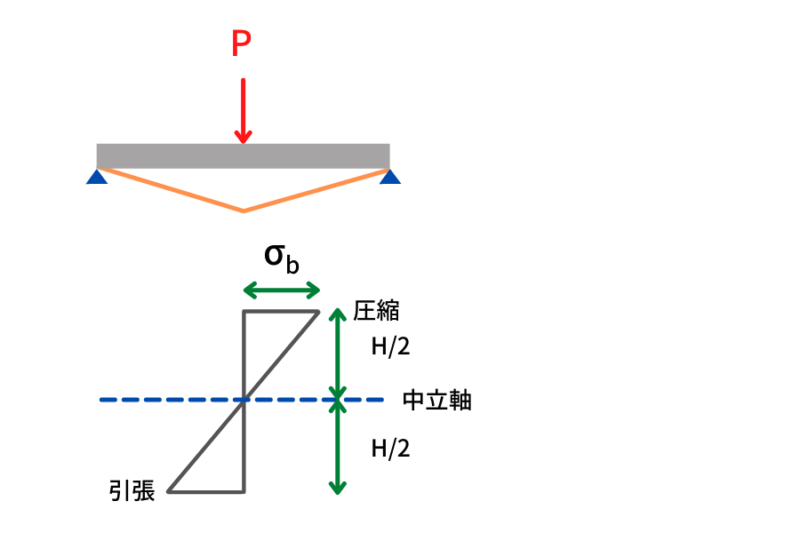
単純梁で中央に集中荷重を受ける部材を細かく見ていくと部材の中立軸を基点にして部材の上側が圧縮で下側が引張になるのが曲げ応力の特徴です
曲げモーメントを受ける部材は全断面に曲げ応力度は発生しますが断面の外側が曲げ応力度最大になり中立軸にかけて応力度が0になります
最も曲げ応力度が大きくなる断面の外端部の曲げ応力度\(\sigma_{b} \)を式に表すと
\(\sigma_{b}=\dfrac{M}{I}y\)になり、
このときの \( I/y \) が断面係数 \( Z \) になるわけで、つまりは
\(\sigma_{b}=\dfrac{M}{Z}\) となります
また先述したようにすべての部材が軸に対して対称な断面ではないので常に中立軸が部材の中央にあるわけではないので注意してください!!
長方形の断面係数
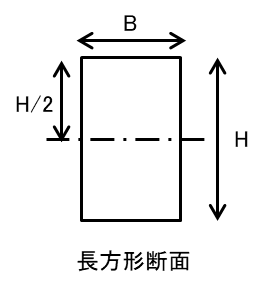
長方形の断面係数は以下の式です
[長方形-断面係数]
\( Z=\dfrac{BH^2}{6}\)
B : 幅
H : せい
導出過程は長方形の断面二次モーメントから算出すると
長方形の断面二次モーメントが\(I=\frac{BH^3}{12}\)で
重心軸からの距離が\(y=\frac{H}{2}\)となるので
\(Z=\dfrac{I}{y}=\dfrac{BH^2}{6} \)
円形の断面係数
円形の断面係数は円形の断面二次モーメントから算出すると以下の式になります
円の断面係数: \(Z=\dfrac{\pi D^3}{32}\)
D : 直径
導出過程は
円の断面二次モーメントが\(I=\dfrac{\pi D^4}{64}\)で
重心軸からの距離が\(y=\dfrac{D}{2}\)となるので
\(Z=\dfrac{I}{y}=\dfrac{\pi D^3}{32} \)
断面係数の計算例
断面係数を使う一級建築士試験の問題を例にし、具体的な使い方を紹介します
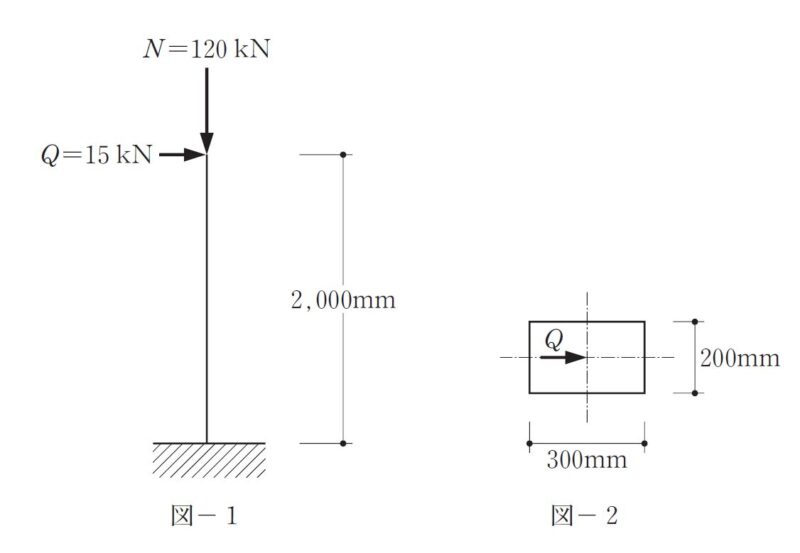
上記の図のような荷重がかかったときの柱脚の応力度を答える問題ですが
曲げ応力度の求め方にフォーカスすると
①柱脚の曲げモーメントMを求める
$$M=Q\times L=15\cdot 10^3\times 2000 = 3.0\cdot10^7 Nmm$$
②断面係数Zを求める
$$Z=B\cdot H^2/6=200\cdot 300^2/6= 3.0\cdot10^6 mm^3$$
③曲げ応力度を求める
$$\sigma_{b}=M/Z= 3.0\cdot10^7/ 3.0\cdot10^6 = 10 N/mm^2$$
曲げモーメントによる圧縮縁および引張縁応力度は±10N/mm2になるということです
加えて軸力Nによる圧縮応力もあるので
$$\sigma_{c}=N/A= 120\cdot10^3/ (300\cdot200) = 2 N/mm^2$$
$$\sigma_{c}=12 N/mm^2 ,\sigma_{t}=8 N/mm^2$$
となります
まとめ
今回は断面係数についてまとめてきました
断面係数を覚えるだけでなく断面二次モーメントと重心軸からの距離で算出できることも併せて覚えておくと忘れた場合でもすぐに導出できると思います
断面係数は一級建築士試験での頻出問題でもあり、曲げ応力度に必要な値です
断面二次モーメントとあわせてしっかりと理解しておきましょう!!


コメント