今回は静定架構・不静定架構とは についてまとめていきたいと思います
一級建築士試験でも計算で不静定次数の問題が出題されることがあります
この記事でわかるように説明したいと思います!!
静定架構とは
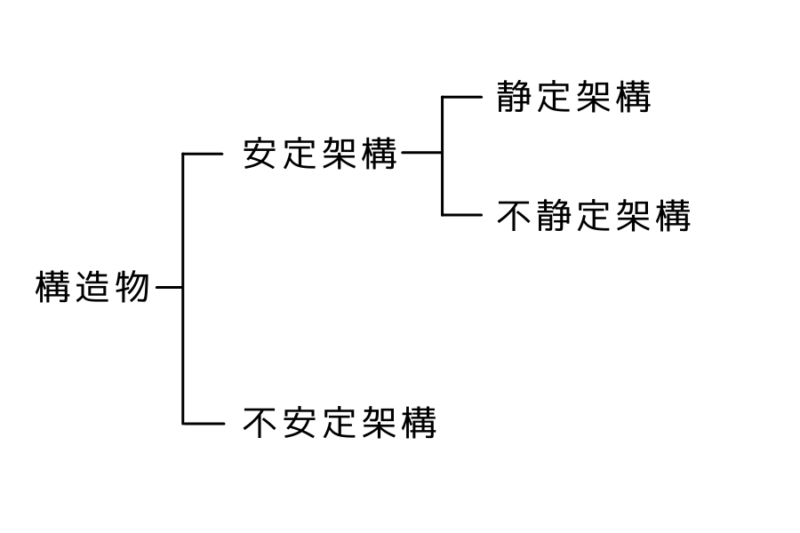
静定架構とは
力とモーメントのつり合い式によって反力・応力を求めることのできる構造物のことを指します
上記の図を見てとれるように安定架構に区分けされます
力のつり合い式とは
ΣW=0のような ある荷重Pがかかったときに逆方向に同じ力の反力Pが現れるつり合い状態で
モーメントのつり合い式とは
ΣM=0のようにピン支点を基点にしたモーメントの合計は0になるつり合い状態を指します
これらの単純な計算によって求まる架構のことを指します!
例えば

上記の図のような単純梁の中央にある荷重Pを作用させたとき考えると
A点・B点それぞれの反力RA・RBとしたとき
力のつり合い式より
ΣW=0 P=RA+RB RA=RB なので
反力はRA=RB=P/2 と求めることができます
モーメントのつり合い式より(梁の長さをLと仮定します)
A点回りのモーメント ΣMa=0 P×L/2-RB×L=0
RB=P/2
梁の中央モーメントMcの大きさは Mc=RA×L/2
Mc=PL/4
と求めることができます
不静定架構とは
不静定架構とは
力とモーメントつり合いだけからでは反力・応力を求めることのできない構造物のことを指します
力・モーメントに加え変形までを考慮することで反力・応力を解くことのできる架構のことを指します!
同じく上記の図を見てとれるように安定架構に区分けされます
例えば

上記の図のような固定梁の中央にある荷重Pを作用させたとき考えると
A点・B点それぞれの反力RA・RB モーメント反力MA・MBをとしたとき
力のつり合い式より
ΣW=0 P=RA+RB RA=RB
対称なので反力はRA=RB=P/2 モーメント反力MA=-MBと求めることができます
モーメントのつり合い式からではモーメントを導出できないので
今回はたわみ角法を用いMA・MBを導出します(梁の長さをLと仮定します)
細かくは省略しますがある点\(x\)のモーメントは
\(\displaystyle M(x)=Px/2-M_{A}…(0\leq x\leq L/2)\)
梁の微分方程式は
\(\displaystyle EI\frac{d^2y}{dx^2}=-M(x)=-Px/2+M_{A}\)
とすることができ
1回積分したわみ角の式に置き換えると
\(\displaystyle EI\theta(x)=-\frac{P}{4}x^2+M_{A}x+C_{1}\)
2回積分したわみの式に置き換えると
\(\displaystyle EIy(x)=-\frac{P}{12}x^3+\frac{M_{A}}{2}x^2+C_{1}x+C_{2}\)
固定端でのたわみ及びたわみ角が0
つまりx=0のとき、たわみ角0・たわみ0の条件が成り立ち
C1=0、C2=0が求まり先ほどの式が
\(\displaystyle EI\theta(x)=-\frac{P}{4}x^2+M_{A}x\)
\(\displaystyle EIy(x)=-\frac{P}{12}x^3+\frac{M_{A}}{2}x^2\)
のようになりました
対称のため中央(x=L/2)でのたわみ角が0になるので
\(\displaystyle EI\theta(L/2)=-\frac{P}{4}\cdot (L/2)^2+M_{A}(L/2)=0\)
したがって
\(\displaystyle M_{A}=-M_{B}=\frac{PL}{8}\)
と求めることができます
少々話がずれましたが不静定架構はこのように少し複雑な計算をしなければ反力を求めることができないということです
静定・不静定の見分け方
静定架構と不静定架構の見分け方は
不静定次数を計算することによって静定・不静定あるいは不安定架構であるかを見分けることができます
不静定次数とは
不静定次数とはある架構が
①静定架構 ②不静定架構 ③不安定架構 どれに該当するかの判別式です
式で表すと
[mathjax]
\( m = n + s + r \ – \ 2k \)
m<0…不安定架構
m=0…静定架構
m>0…不静定架構
m:不静定次数
n:反力数 固定は3・ピンは2・ローラーは1
s:部材数
r:剛節点数
k:節点数
これだけでは文字の羅列だけですので分かりづらいく、本質とずれています
不静定次数=反力数+部材数+剛節点+節点×2
のように覚え、節点数だけは-2倍するとだけ覚えましょう
反力数:n
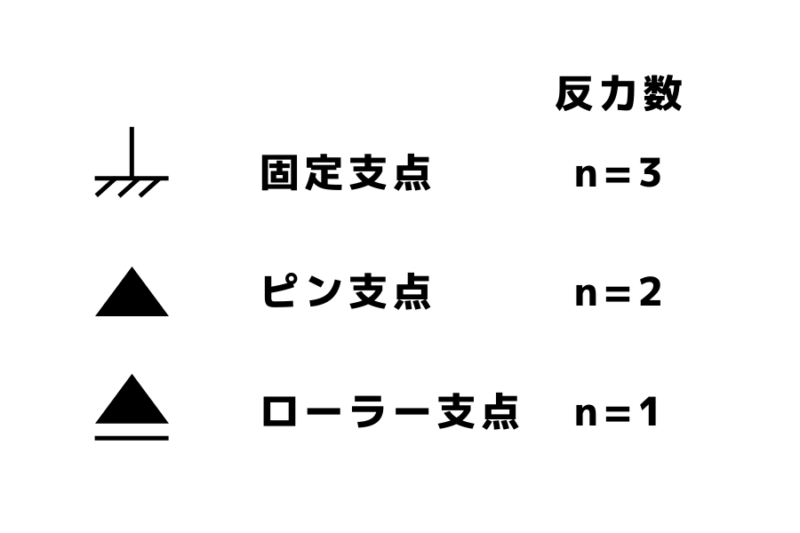
反力数は支点の拘束条件によって変化します
固定点は反力数3
ピン支点は反力数2
ローラー支点は反力数1
固定はモーメント・水平・鉛直を拘束するから3
ピンは水平・鉛直を拘束するから2
ローラーは鉛直のみで1
と覚えるのがいいでしょう
ちなみに反力数n=0はないので気を付けましょう!
部材数:s
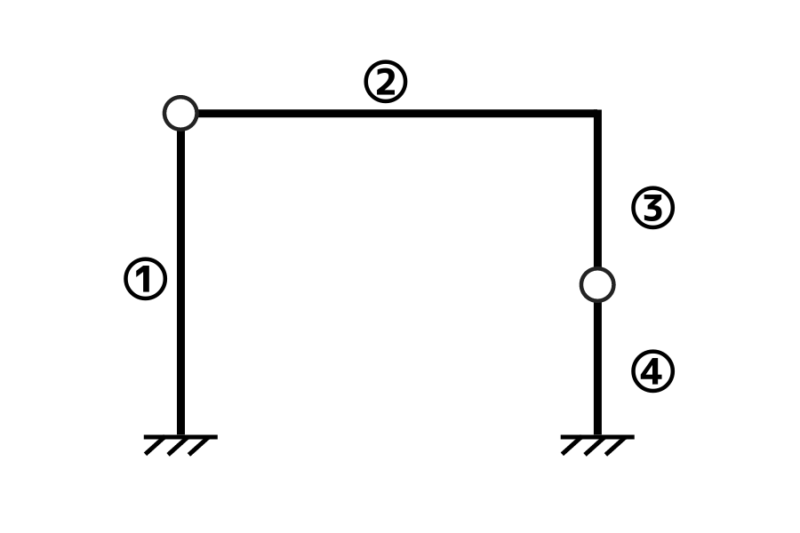
部材数はそのままの意味で架構を形成する線の数を指します
線の数と覚えましょう
注意すべき点は一本の直線であっても途中にピン節点がある場合は部材数は2つに分けられます
上図の場合は s=4 です
剛節点数:r
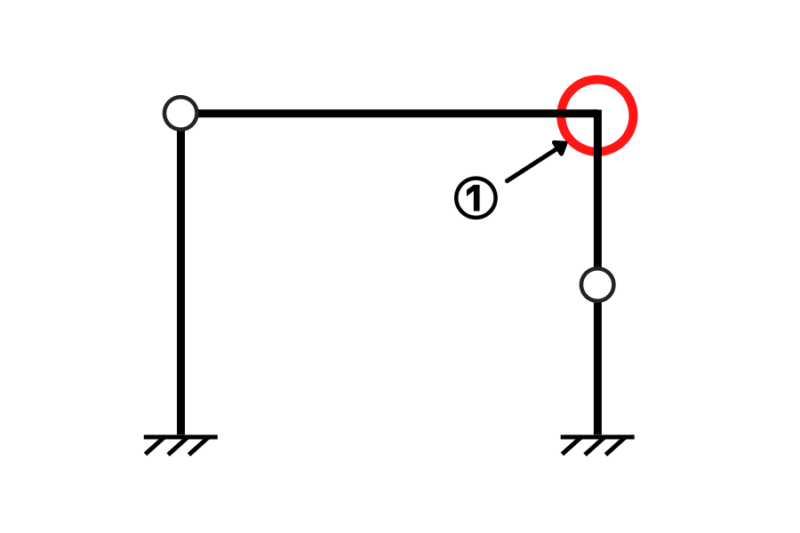
剛節点(英:rigid)とは互いの部材が自由に回転できないよう拘束したつなぎ目を意味します
剛節点の対義語はピン節点です
簡単に言えばピン節以外で折れ曲がっている箇所を指します
間違えやすいことは剛節点数に固定支点は含めないことです!!
上図の場合は r=1 です
節点数:k
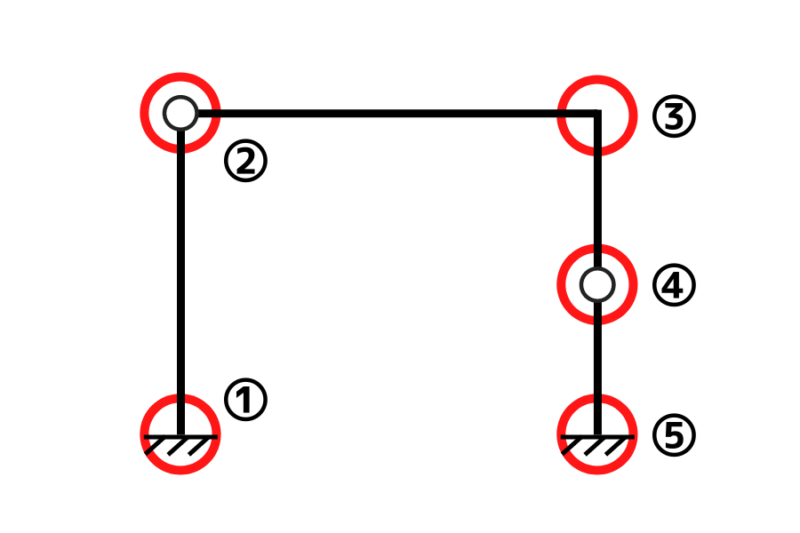
節点(英:knot)とは部材のつなぎ目・結び目を意味します
シンプルに言えばピンや剛であっても折れ曲がっている箇所を指します
間違えやすいことは節点数に支点は含めることです!!
上図の場合は k=5 です
例題:不静定次数
これまでの知識で一級建築士試験の不静定次数問題は解けると思います
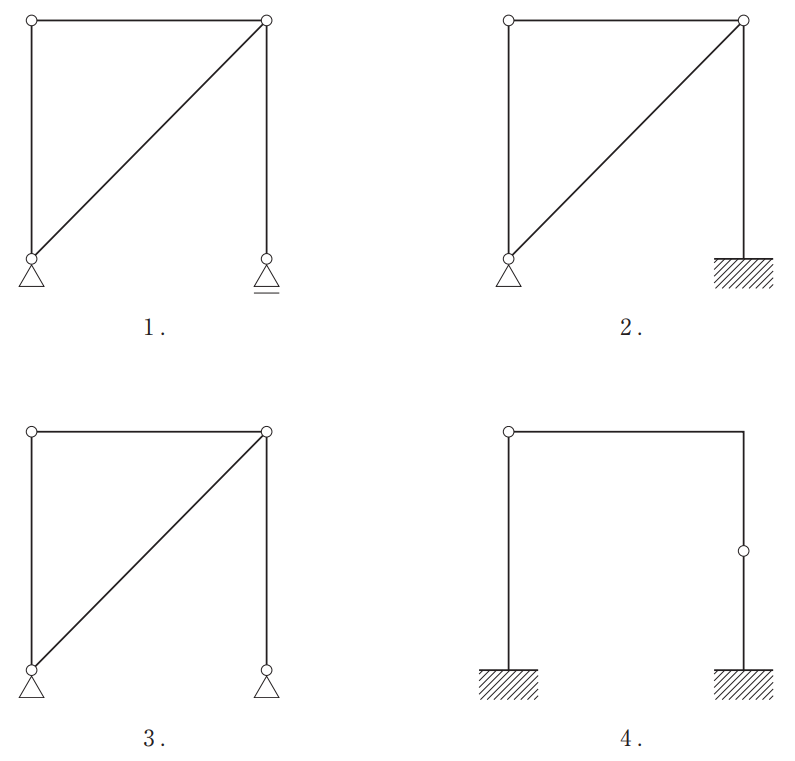
この中で静定架構はどれかという問題です
解答例
1:n=2+1=3, s=4, r=0, k=4, m=3+4+0-2×4=‐1 →不安定架構
2:n=2+3=5, s=4, r=0, k=4, m=5+4+0-2×4=1 →不静定架構
3:n=2+2=4, s=4, r=0, k=4, m=4+4+0-2×4=0 →静定架構
4:n=3+3=6, s=4, r=1, k=5, m=6+4+1-2×5=1 →不静定架構
となり答えは③番でした
まとめ
今回は静定・不静定架構についてまとめてきました
静定架構は力・モーメントのつり合いから算出できる一般的な架構を指します
建築士試験でも計算問題として出されるのはせいぜい静定架構の問題です
不静定架構となるとたわみ角法や固定法が必要になる少々難しい架構を指します
静定・不静定の見分け方は不静定次数によって判別できます
不静定次数は一級建築士試験でも頻出問題であるのでしっかりと理解しましょう
余談ですが実務ではほとんど使いません!!


コメント