今回は構造の崩壊荷重についてまとめていきたいと思います。
崩壊荷重は一級建築士の学科試験の構造でよく出題されます。『仮想仕事の原理』などの聞き慣れない言葉も多くあるので難しいと印象を持つ人も少なくありません。
この記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

崩壊荷重の計算ってどうやるんだっけ!?
崩壊荷重とは
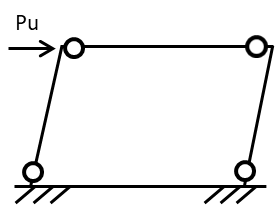
崩壊荷重とは崩壊メカニズム時の荷重を指します。言い換えると建物や構造物は外力(荷重)に対して無限に耐えられることはなく、いつか崩壊します。
ある一定の外力(荷重)で梁や柱が降伏していき塑性ヒンジができ、それ以上の耐荷重を増やすことができなくなり『荷重が増えず変形だけが進んでいく状態』や『梁や柱の部材が破壊され一気に崩壊する状態』になる荷重を崩壊荷重といいます。
崩壊荷重の記号は[P] や[Pu]で表現されます。Puの”u”はultimateつまり“終局”の意味を表します。単位は力の[kN]または[N]と表現されます。
崩壊メカニズムとは
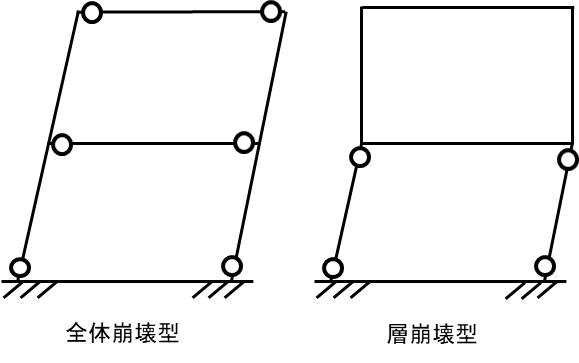
崩壊メカニズム(別名:崩壊形・崩壊機構)とは塑性ヒンジが形成された状態の架構モデルを指します。
崩壊メカニズムは実際に計算や解析しなければどこにヒンジができどのような崩壊型になるかはわかりませんがヒンジができる条件として部材にかかる応力が大きく、部材耐力(部材の全塑性モーメント)が小さいところから順にヒンジは発生していきます。
崩壊メカニズムにも以下ような種類があります。
- 全体崩壊型
- 層崩壊型
構造の世界では全体崩壊型が望ましいといわれており、全体崩壊型は外力(荷重)がかかったときにいきなり壊れるのではなく、建物の変形が進み地震のエネルギーを吸収し、徐々に崩壊していく理想的な崩壊型です。
層崩壊型は層の柱頭・柱脚に塑性ヒンジができその柱のある層の変形だけが進み、柱が壊れてしまうとその層がつぶれてしまうので建物全体が一気に壊れる脆性破壊と呼ばれ非常に危険な崩壊型と覚えておきましょう!
塑性ヒンジとは

塑性ヒンジ(英:plastic hinge)とは荷重が加えられ梁や柱などの部材が全塑性モーメントに達すると部材耐力以上は曲げ応力が増えていかず変形が進んでいきます。
変形が進むことはつまり部材が回転自由となるピン支点のような状態になります。つまり部材が塑性しピンのような状態になる箇所を塑性ヒンジといいます。『塑性ヒンジ=ピン』と考えて違いないでしょう。
塑性ヒンジは曲げモーメント図の最大のところから発生します。ヒンジは日本語で蝶番の訳なのでイメージがつきやすくなるのではないでしょうか!?

全塑性モーメントについてはこちらの記事を参照ください。
崩壊荷重の求め方
一級建築士試験の問題でよく出題される崩壊荷重の求め方は仮想仕事の原理に基づきます。
仮想仕事の原理とは簡単に言えば外力と内力のつり合った状態を指します。式で表すと
仮想仕事の原理
\(Σ(Pu×\delta)=Σ(Mp×\theta)\)
Pu:崩壊荷重
δ:変位量あるいは変形量
Mp:全塑性モーメント
θ:たわみ角
崩壊荷重の求め方は
- 崩壊荷重時の変形量・たわみ角を仮定する
- 外力(荷重)の仕事量ΣP×δの式をつくる
- 内力(部材耐力)の仕事量ΣM×θの式をつくる
- 仮想仕事の原理の等式(ΣP×δ=ΣM×θ)から導く
具体的な実際の問題から解いていきましょう!
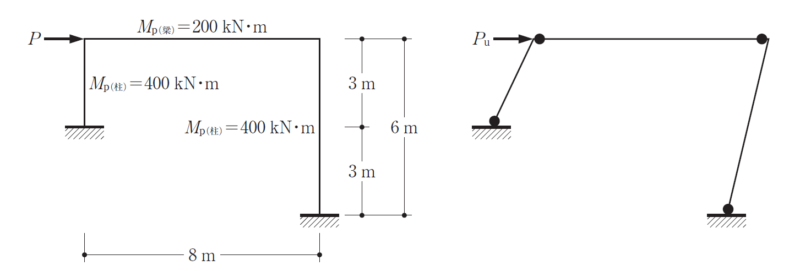
梁の全塑性モーメントは200kNm 柱の全塑性モーメントは300kNmで水平荷重Pが作用しており、図の右のような崩壊メカニズムになった場合の崩壊荷重Puを求める問題です。
余談ですがこのときのは梁端部が先に降伏する(全塑性モーメントに達する)全体崩壊型になります。
1.崩壊荷重時の変形量・たわみ角を仮定する
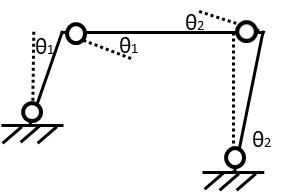
まず崩壊荷重時の層全体の変形量を\(\delta\)と仮定します。
つぎにたわみ角を仮定してます。
左の柱のたわみ角をθ1,右の柱のたわみ角をθ2とします。
柱頭の変位量が同じになるので、
\(\delta=sin\theta_{1}\cdot 3=sin\theta_{2}\cdot 6\) とおきます。
ただしたわみ角θが微小であることに限ればsinθ≒θとなるので、
\(\delta=\theta_{1}\cdot 3=\theta_{2}\cdot 6\) …(1)
となります。この式を解くと
\(\theta_{2}=\theta_{1}/2\) となります。
2.外力の仕事量の式を作る
つぎに外力の仕事量の式を作ります。
外力の仕事量は荷重×変位で表されます。したがって
\(\Sigma W=Pu\cdot\delta\) …(2)
3.内力の仕事量の式を作る
つぎに内力の仕事量の式を作ります。
内力とは部材自身の持つエネルギーのようなもので内力の仕事量は全塑性モーメント×部材のたわみ角で表されます。
またたわみ角はヒンジのあるところに存在します。柱のたわみ角は簡単に見つかりますが、梁のたわみ角は柱梁が直角に交わる場合は接合部角度を90°に保ちながら水平力を受けた際にどのような角度がつくかを想像して描きます。内力を式で表すと
\(\Sigma W=400\cdot\theta_{1}+200\cdot\theta_{1}+200\cdot\theta_{2}+400\cdot\theta_{2}\)
たわみ角は先ほど \(\theta_{2}=\theta_{1}/2\) となったので以下のように変形し、
\(=400\cdot\theta_{1}+200\cdot\theta_{1}+200\cdot\theta_{1}/2+400\cdot\theta_{1}/2\)
\(\Sigma W=900\cdot\theta_{1}\) …(3)
4.仮想仕事の原理の等式から導く
(1)~(3)式をまとめ、仮想仕事の原理の等式から導くと
\(\delta=3\cdot\theta_{1}\)
\(Pu\cdot\delta=900\cdot\theta_{1}\)
崩壊荷重Puとしてあらわすと
\(Pu=\dfrac{900\cdot\theta_{1}}{3\theta_{1}}=300\)
別解
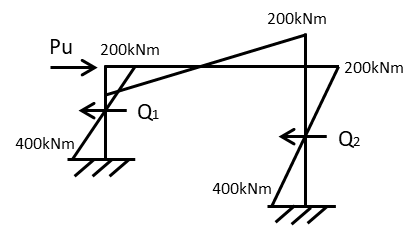
このほかにも柱にかかるせん断力を利用して答えを導く方法もあります。崩壊荷重(水平荷重)=柱のせん断力の合計 を利用して解いていく方法です。
まずM図を描きます。M図は引張側にモーメント応力が来るように描き、柱梁接合部は(梁の全塑性モーメント)<(柱の全塑性モーメント)ため梁の全塑性モーメントにして描きます。柱脚は柱の全塑性モーメントです。
柱にかかるせん断力はせん断力=柱のモーメント÷柱の長さ で表されるので
左柱のせん断力:\(Q_{1}=(400+200)/3=200\) kN
右柱のせん断力:\(Q_{2}=(400+200)/6=100\) kN
崩壊荷重(水平荷重)=柱のせん断力の合計より
崩壊荷重:\(Pu=Q_{1}+Q_{2}=300\) kN とより簡単に解くことができます!
2層ラーメン構造の問題
最後に全塑性モーメントの派生型として2層ラーメン構造の問題が近年よく出題されます。
基本的には先ほど紹介した解き方で解けますが架構の鉛直反力や梁のせん断力を問われる場合は少しばかり余分な知識がいるので一緒に解説したいと思います。
実際の一級建築士の問題から解いてみましょう!
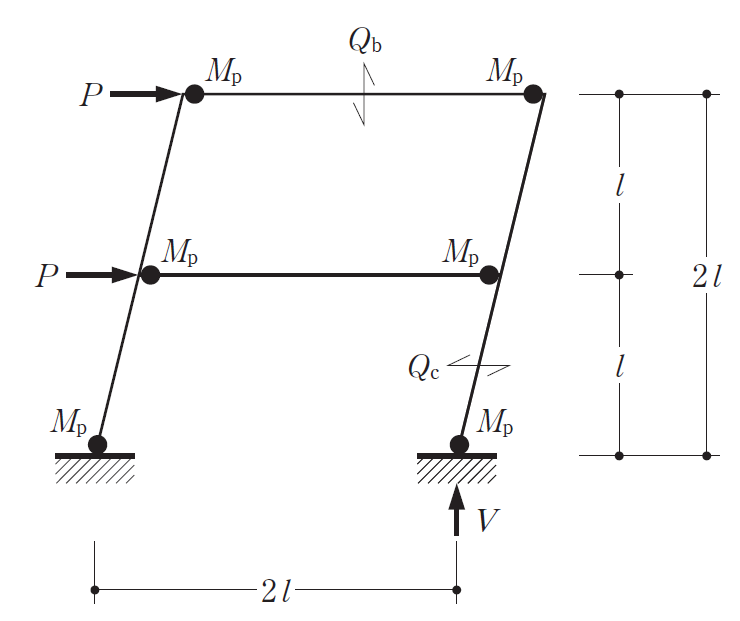
この問題では梁のせん断力をQb・鉛直反力V・崩壊荷重P・柱のせん断力Qcの4つを求める問題です。
この問題の解き方は
- 梁のせん断力Qbを求める
- 梁のせん断力から鉛直反力Vを求める
- 仮想仕事の原理から崩壊荷重Pを求める
- 崩壊荷重Pから柱のせん断力Qcを求めます
ではやってみましょう。
1.梁のせん断力Qbを求める
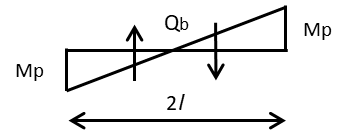
まず初めに梁のせん断力を求めていきましょう。梁のせん断力=梁のモーメント÷梁の長さで求められるので
\(Qb=\dfrac{Mp+Mp}{2l}=\dfrac{Mp}{l}\)
2.梁のせん断力から鉛直反力Vを求める
つぎに梁のせん断力から鉛直反力を求めていきましょう。力のつり合いより鉛直反力にかかる荷重がないため
右下の鉛直反力=2層の梁の右端のせん断力+1層の梁の右端のせん断力 で求められます(注:鉛直荷重があるとこの等式は成り立ちません)
2層の梁のせん断力は先ほど求めたので、1層の梁のせん断力を求めます。
\(Qa=\dfrac{Mp+Mp}{2l}=\dfrac{Mp}{l}\)
つまり
\(V=Qa+Qb=2\dfrac{Mp}{l}\)
一方の左下の鉛直反力は-2Mp/l になります。
3.仮想仕事の原理から崩壊荷重を求める
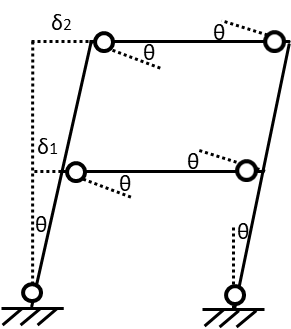
つぎに仮想仕事の原理から崩壊荷重Pを求めます。
変位量・たわみ角を仮定し
1層のたわみ角:\(δ_{1}=θ・l\) …(a)
2層のたわみ角:\(δ_{2}=θ・2l\) …(b)
外力の仕事量は
\(\Sigma W=P\cdot δ_{1}+P\cdot δ_{2}\) …(c)
内力の仕事量は
\(\Sigma W=(Mp\theta+Mp\theta+Mp\theta)×2=6Mp\theta\) …(d)
(a)~(d)の式をまとめると
\(P\cdot δ_{1}+P\cdot δ_{2}=6Mp\theta\)
\(P\cdot\theta l+P\cdot\theta ・2l=6Mp\theta\)
\(P=\dfrac{2Mp}{l}\)
4.崩壊荷重Pから柱のせん断力Qcを求める
最後に崩壊荷重Pが求まったことで柱のせん断力を求めます。
崩壊荷重(水平荷重)=柱のせん断力の合計より1層の柱の長さおよび全塑性モーメントのが同じであるので柱の剛性等しくなるので右左の柱せん断力は等しくなり、したがって
\(2P=Qc+Qc=2Qc\)
\(P=\dfrac{2Mp}{l}\)
\(Qc=\dfrac{2Mp}{l}\)
まとめ
今回は崩壊荷重についてまとめてみました。
崩壊荷重は仮想仕事の原理から算出でき、架構に塑性ヒンジを形成し崩壊するときの荷重です
崩壊荷重の求め方は
- 崩壊荷重時の変形量・たわみ角を仮定する
- 外力(荷重)の仕事量ΣP×δの式をつくる
- 内力(部材耐力)の仕事量ΣM×θの式をつくる
- 仮想仕事の原理の等式(ΣP×δ=ΣM×θ)から導く
基本はこれで解くことができます。崩壊荷重は理解が難しい分野ではありますが計算自体は難しくないため、他の受験生と差をつけられる問題です
ぜひ何度も読み直し理解してみて下さい!!




コメント