今回は2022年度一級建築士 学科試験Ⅳ構造のNo.1の問題についてまとめていきたいと思います。
今回は材料力学の応力の問題から出題されています。
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

構造の問1:全塑性モーメントってなんだっけ!?
問題 No.1
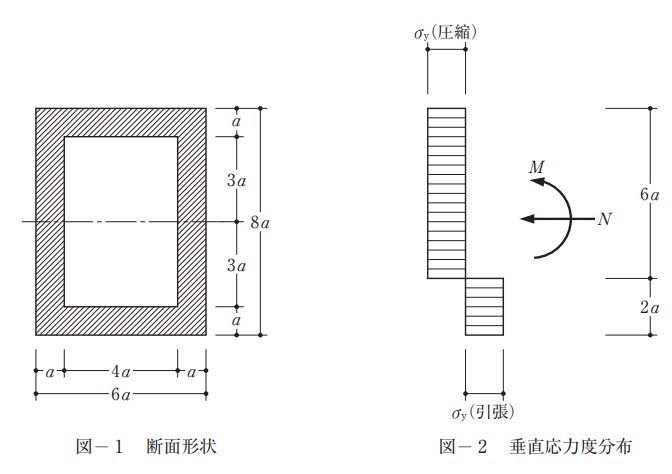
図-1 のような等質な材料からなる部材の断面が、図-2 に示す垂直応力度分布となって全塑性状態に達している。このとき、断面の図心に作用する圧縮軸力Nと曲げモーメントMとの組合せとして、正しいものは、次のうちどれか。ただし、降伏応力度はσyとする。
[選択肢] 鉛直荷重N モーメント荷重M
- \(N:8a^2 \sigma_{y}\quad M:42a^3 \sigma_{y}\)
- \(N:8a^2 \sigma_{y}\quad M:52a^3 \sigma_{y}\)
- \(N:12a^2 \sigma_{y}\quad M:42a^3 \sigma_{y}\)
- \(N:12a^2 \sigma_{y}\quad M:52a^3 \sigma_{y}\)
この問題キーワードは
- 圧縮応力と曲げ応力が同時に作用する
- 塑性断面係数の算出のしかた
前提条件
この問題はまず全塑性モーメントと塑性断面係数について理解する必要があります。
全塑性モーメント
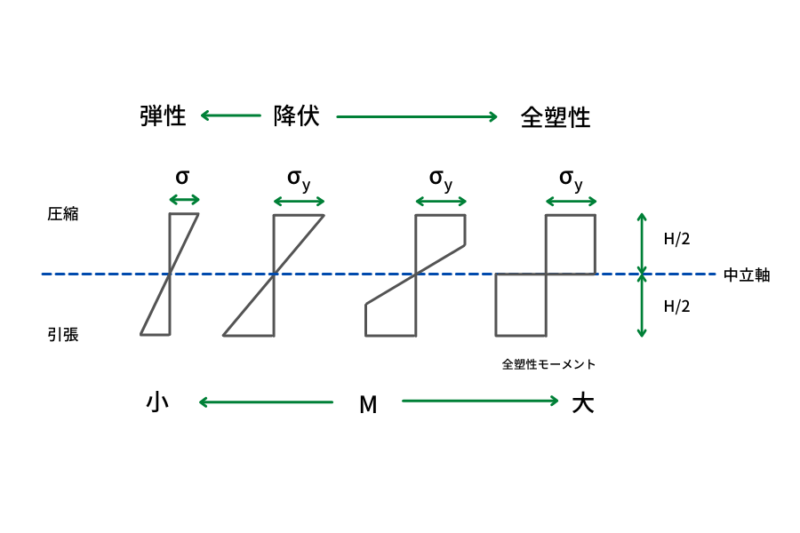
全塑性モーメント(英:full plastic moment)とは上図の右にあるような状態で部材断面が完全に塑性化したときのモーメントのことを指します。
塑性とは部材が降伏点を超えた場合、力をさらに変形が進みもとの形状に戻らない状態を指します。
弾性とは力を除した後もとの形状に戻る状態を指します。
図のように曲げモーメントMが作用させたときに曲げ縁応力は\(\sigma\)になります。断面に作用するMが徐々に大きくなると図の右側のように進んでいきます。
そして断面のもっとも外側の最外縁応力度がこれ以上増えることのない降伏強さ\(\sigma_{y}\)に達します。この時のモーメントを降伏モーメントMy(英:yield moment)と呼びます
断面縁から順に塑性化していき最終的に断面すべてが塑性化する全塑性状態になります。全塑性状態時のモーメントのことを全塑性モーメントといいます。
塑性断面係数の求め方
塑性断面係数の求め方は(圧縮or引張断面積)×(断面積を2等分する軸から断面図芯からの距離)で求めることができます。図に示すと
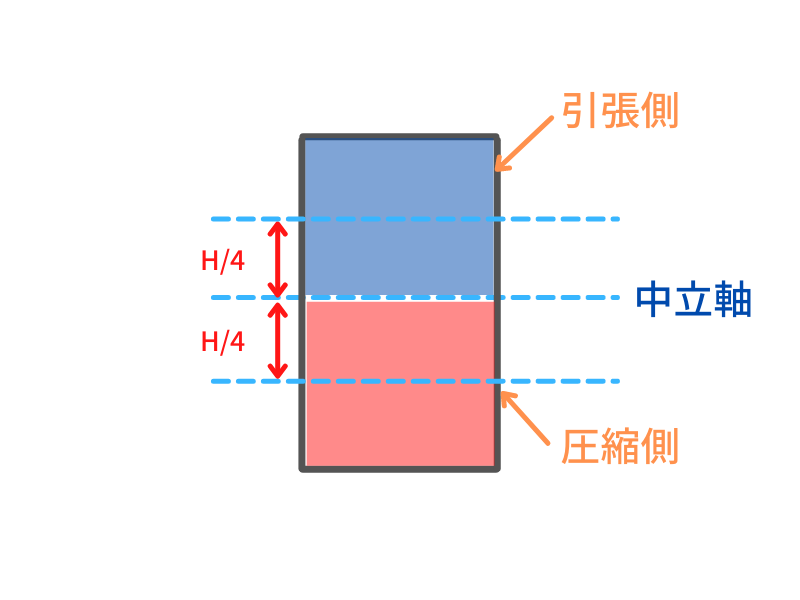
このようになり簡単な長方形断面でBが幅、Hがせいとした場合、圧縮・引張側のそれぞれの断面積は\(BH/2\) 、断面を2等分する中立軸からの距離は\(H/4\)
\(BH/2 × H/4 ×\) 2ヶ所 になるので
\(Zp=\dfrac{BH^2}{4}\) と導出できると思います
塑性断面係数の求め方に重要な考え方があります。それが全断面降伏時の中立軸は断面の軸応力度の合力が0であることです。式で表すと
\(Zp=\int_{At} |\xi|dA+\int_{Ac} |\xi|dA\)
Ac At:圧縮・引張断面積
ξ:中立軸からの距離
シンプルに言い換えると引張側と圧縮側の断面積が一致します。
対称的な断面の場合は重心軸で圧縮と引張の境界線があるので重心軸を基点になり、非対称断面の場合は断面を2等分する軸を基点になります。
間違えやすいのは”重心軸と中立軸は常に一致はしない”ことです。詳しい内容はこちらの記事を参考にしてみて下さい。
解き方
今回の問題の解く順序は
- 曲げを負担する圧縮と引張の範囲を明確にする
- 偶力の公式から部材にかかる全塑性モーメントを求める(Mp=A・σy・j)
- 残りの応力度から軸力を求める(N=A・σy)
ひとつずつ算出していきましょう。
まずは断面が負担する圧縮と曲げの範囲を明確にします。圧縮(あるいは引張)と曲げモーメントを同時に受ける部材で全塑性モーメントまで応力を増やしていき、最終的な全塑性状態の応力度分布は上記の図で示したように分けることができます。
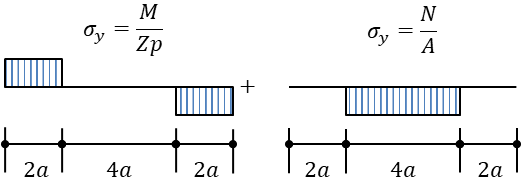
曲げ側負担分と圧縮側担分の範囲の見分け方は曲げ側負担部分に生じる引張側の距離を参照します
理由は曲げと圧縮を同時に作用させたときに引張応力が生じると同時に必ず曲げ応力度がはたらいているためです。圧縮力だけでは引張応力度は生じません!!
引張側が距離 \(2a\) とわかれば曲げによる圧縮側も同じく \(2a\) となり
曲げによる負担範囲は両端から \(2a\) の範囲になり
圧縮による負担範囲は残った \(4a\) の範囲になります。
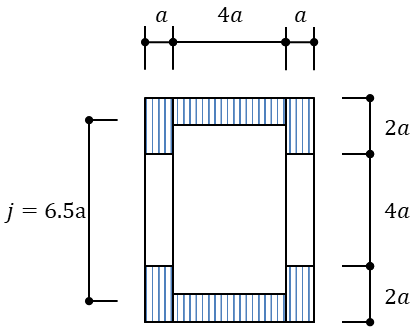
つぎに曲げを負担範囲から塑性断面係数を求めます。塑性断面係数の公式より
\(Z_{p}=A_{b}\cdot j\)
jは応力中心間距離で断面一次モーメント(重心位置)から求める必要があります。Abは曲げ応力用断面積を表します。図を参考にして解くと
\(j=4a+1.25a\cdot 2=6.5a\)
\(A_{b}=2a\cdot a\cdot 2+4a\cdot a=6a^2\)
\(Z_{p}=52a^3\)
曲げ応力度の公式より
\(\sigma_{y}=\dfrac{M}{Z_{p}}\)
\(M=\sigma_{y}\cdot Z_{p}\)であり、式をまとめると
\(M=52a^3\sigma_{y}\)
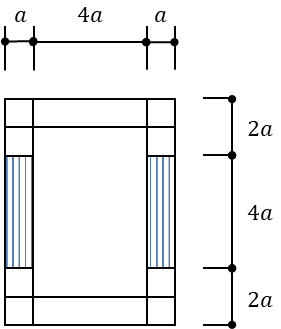
つぎは圧縮側の応力度を計算します。まずAcを求めます、Acは軸応力用断面積を表します。
\(Ac=4a\cdot a\cdot 2=8a^2\)
Nは軸力(圧縮力)は圧縮応力度の公式より
\(\sigma_{y}=\dfrac{N}{Ac}\)
\(N\)の式にすると
\(N=8a^2 \sigma_{y}\)
上記をまとめると答えは②となります。
まとめ
今回は2022年 一級建築士 学科試験Ⅳ構造 No.1の解説をしてきました
今回の問題のポイントは塑性断面係数の算定のしかたです。普段見慣れない計算方法で解くのが難しく感じるかもしれませんがひとつずつ紐解いていけば簡単な問題です。
ぜひ何度も読み返し解けるのようになって下さい!!
こちらは類似の問題ですので参考にしてみて下さい。
対策
- 断面がH型断面になった場合
- 応力中心間距離jの出し方について
こちらも自分で問題を作って解いてみるとよいでしょう!!




コメント