今回は2021年度一級建築士 学科試験Ⅳ構造のNo.3の問題についてまとめていきたいと思います
今回は構造力学の力のつり合い式・モーメントのつり合い式から出題されています
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
問題 No.3
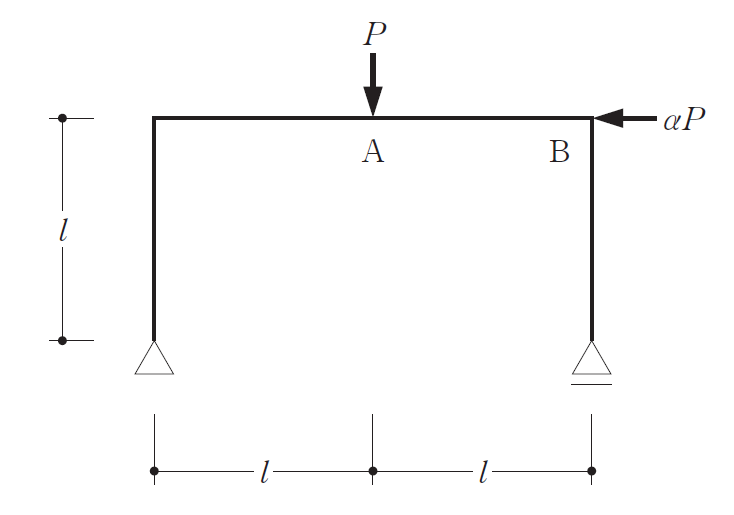
[No.3]
図のようなラーメンにおいて、A点に鉛直荷重P 及びB点に水平荷重αP が作用したとき、A点における曲げモーメントが0 になるためのα の値として、正しいものは次のうちどれか。
ただし、全ての部材は全長にわたって等質等断面の弾性部材とし、自重は無視する。
[選択肢]
1 α=1/2
2 α=1
3 α=3/2
4 α=2
この問題キーワードは
- A点における曲げモーメントが0であること
- モーメントのつり合いをどこを基点にするか
だと思います。細かく解説していきます
前提条件
この問題は
・力のつり合い式
・モーメントのつり合い式
についての知識が問われています。個人的にも本テストの中でも最も簡単に解ける問題だと思います
力のつり合い
力がつり合う(静止や等速直線運動のような)状態は荷重=反力になる、つまり力の合計は0であることです
力のつり合い式は基本的には2軸つまり鉛直方向と水平方向で考えます
数式で表すならば
鉛直方向:\(\Sigma V=0\)
水平方向:\(\Sigma H=0\)
V:鉛直方向の力
H:水平方向の力
モーメントのつり合い
モーメントがつり合いは曲げを負担しない支点まわりのモーメントはつり合った状態になることつまりモーメントの合計は0であることです
基点はピン支点やローラー支点周りに考えます。モーメントのつり合いを解く場合は時計回りを+・反時計回りをーのように設定する必要があります(逆でも問題ないです)
数式で表すならば
モーメントのつり合い:\(\Sigma M=0\)
M:ピン支点またはローラー支点周りのモーメント
解き方
解く順序は
- 力のつり合い式より鉛直・水平反力の算出
- モーメントのつり合い式をたてる
- 力のつり合い式とモーメントのつり合い式の連立方程式を解く
ひとつずつ解いていきましょう
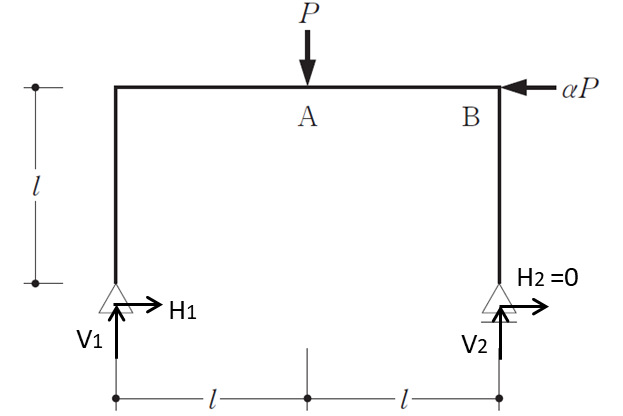
まずは鉛直方向の反力の算出です。左の鉛直反力をV1・右の鉛直反力をV2とし、式をたてると
\(\Sigma V=0\)
\(P=V_{1}+V_{2}\) …(1)
つぎに水平方向の反力の算出です。左の水平反力をH1・右の水平反力をH2とし、また右の支点はローラー支点なので\(H_{2}=0\)です
\(\Sigma H=0\)
\(\alpha P=H_{1}\) …(2)
つぎにモーメントのつり合い式をたてます。問題文よりA点のモーメントが0になるαの値を見つけるのでA点をピン支点と仮定しても同じことが言えます
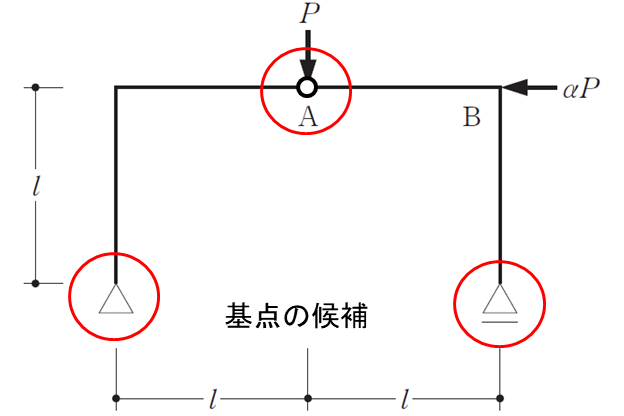
まずはつり合い式をたてるための基点の候補として
・右の支点
・左の支点
・A点
が候補に挙がります。このときにどこの支点がよいかと言えば未知数が少ないところから解くとより簡単に解くことができます。(未知数が2つでも普通に解くことができます。)
①右の支点としたときは未知数がαPとV2の2つ
②左の支点としたときは未知数がαPとV1の2つ
③A点としたときの左側は未知数がH1とV1の2つ
④A点としたときの右側は未知数がV2の1つだけ
となるので、④A点としたときの右側のモーメントのつり合い式をたてることにします
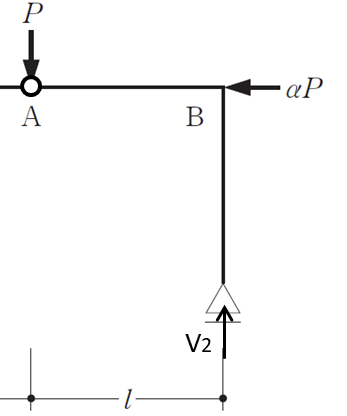
\(\Sigma Ma=0\)
\(V_{2}\cdot l=0\)
したがって
\(V_{2}=0\)
V2がわかったところで(1)式より
\(P=V_{1}\)
さいごにA点としたときの左側モーメントのつり合い式をたてると
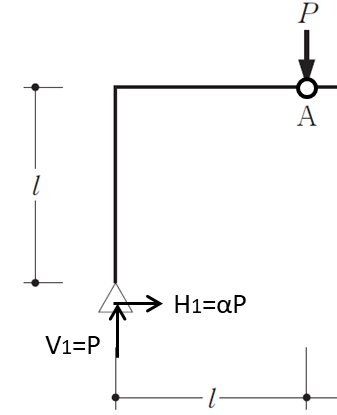
\(\Sigma Ma=0\)
\(V_{1}\cdot l – H_{1}\cdot l=0\) …(3)
(2)式・(3)式より
\(P\cdot l – \alpha P\cdot l=0\)
\(\alpha=1\)
したがって最終的な答えは②でした
まとめ
今回は2021年 一級建築士 学科試験Ⅳ構造 No.3の解説をしてきました
今回のポイントはA点における曲げモーメントが0であることとモーメントのつり合いをどこを基点にするかです。
この問題は構造力学でも初歩的かつ基本的で力のつり合い式とモーメントのつり合い式だけで解ける問題です。是非とも間違えずに答えてもらいたい問題です




コメント