今回は2021年度二級建築士 学科試験Ⅲ建築構造のNo.2の問題についてまとめていきたいと思います
今回は材料力学の曲げ応力度の問題から出題されています
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
問題 No.2
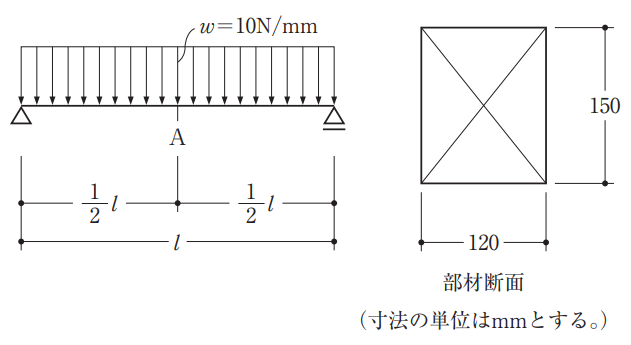
[No.2]
図のような等分布荷重を受ける単純梁に断面 120mm×150mmの部材を用いた場合、A点の最大曲げ応力度が 1 N/mm2となるときの梁の長さlの値として、正しいものは、次のうちどれか。ただし、部材の断面は一様とし、自重は無視するものとする。
[選択肢]
1. 300mm
2. 600mm
3. 900mm
4. 1200mm
5. 1500mm
この問題を解くためのキーワードは
- 単純梁ー等分布荷重の曲げモーメント
- 曲げ応力度
前提条件
この問題を解くためには曲げモーメントと算出と曲げ応力度の関係性を覚えておく必要があります
単純梁-等分布荷重の曲げモーメント
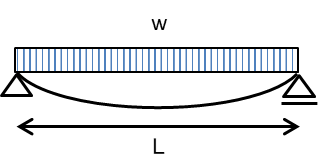
等分布荷重は梁の全長にかかる均一の荷重のことを指し、記号は[w]で表し、単位は力/長さで[kN/m]や[N/mm]のように表します。
単純梁の等分布荷重の中央の曲げモーメントの公式は
[単純梁‐等分布荷重‐中央曲げモーメント]
\(M=\dfrac{wL^2}{8}\)
w:等分布荷重
L:梁長さ
もし単純梁‐等分布荷重の公式を忘れてしまっても、支点反力を計算し、M(x)の式を立てることで簡単に求めることができます。
曲げ応力度
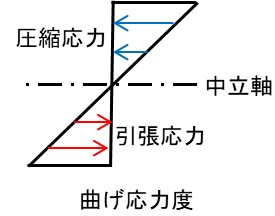
曲げ応力度とは曲げモーメントを受ける部材の断面内にはたらく引張側と圧縮側の応力度を指します。
記号は[σb]で表し、単位は[N/mm2]で表します。
[曲げ応力度] \(\sigma_{b}=\dfrac{M}{Z}\)
M:曲げモーメント(N・mm2)
Z:断面係数(mm3)
断面係数
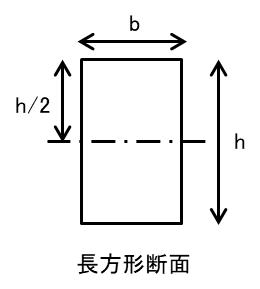
断面係数(英:elastic section modulus)は断面による曲げに対する抵抗値と表現できます。断面係数が大きければ曲げ応力度は小さくなり、断面係数が小さければ曲げ応力度は大きくなるという特徴があります。もともとは断面二次モーメントから導出された値です。
記号は[Z]で表し、単位は[mm3]や[cm3]で表すことが多いです
式で表すと
[断面係数‐長方形]
\(Z=\dfrac{bh^2}{6}\)
b:幅(mm)
h:せい(mm)
詳しい解説はこちらを参考にしてください
解き方
解く方法順序は
- 断面係数を計算する
- 最大曲げモーメントの式を立てる
- 曲げ応力度を1N/mm2 とし計算する
ひとつずつ算出していきましょう
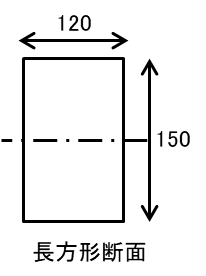
まず与えられた長方形断面の断面係数を計算します。
\(Z=\dfrac{120\times 150^2}{6}=4.5\times 10^5\) …(1)式
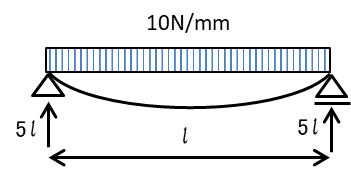
さらに最大曲げモーメントの計算をしていきます。
支点反力は鉛直方向の力のつり合い式より
\(V=10\cdot l/2=5l\)
支点より\(x\)進んだ距離でのモーメントM(x)の式を立てると
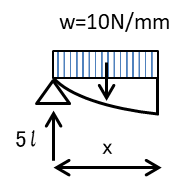
\(M(x)=5lx-10x(x/2)=5x(l-x)\)
曲げモーメントは梁中央にて最大となるので\(x=l/2\)を代入します。もちろん覚えていれば単純梁-等分布荷重の曲げモーメントの公式を用いて下さい。
\(M(l/2)=5(l/2)(l-l/2)=\dfrac{5l^2}{4}\) …(2)式
最後に\(l\)を求めていきます。
\(\sigma_{b}=\dfrac{M}{Z}\)
(1)(2)式より
\(1.0=\dfrac{5l^2/4}{4.5\times 10^5}\)
\(l^2=36\times 10^4\)
\(l=600\)
したがってまとめると『l=600mm』となり、最終的な答えは②でした
まとめ
今回は2021年 二級建築士 学科試験Ⅲ建築構造 No.2の解説をしてきました。
今回の問題は曲げ応力度から部材長さを決定するいつもと逆のパターンの問題です。曲げ応力度の算定のしかたは非常に重要であり二級建築士に求められる必須の知識です。曲げモーメントの算出のしかたも力学の中では基本中の基本であるので、もし忘れてしまった方は是非とも解けるようにしてください!!
断面係数とはの記事もあわせて参考にしてみて下さい
・曲げ応力度が与えられ等分布荷重wを求める場合
・集中荷重になる場合
・断面が円形の場合
こちらも自分で問題を作って解いてみるとよいでしょう!!




コメント