今回は許容曲げ応力度についてわかりやすく解説していきたいと思います。
許容曲げ応力度は鋼構造を設計する際に使うとても重要な知識です。ぜひこの記事を参考にしてみて下さい！！
許容曲げ応力度ってなんだ？？
許容曲げ応力度fbとは
許容曲げ応力度とは許容応力度設計における許容される応力度つまり、建築基準法で定められた曲げモーメントの応力度です。
許容曲げ応力度は引張応力度とは異なり、横座屈が発生するので単純に基準強度に安全率をかけただけでは算出できないので注意が必要です。
許容応力度設計とは建築基準法施行令第81条2項二のイに規定される設計法で鋼構造においては降伏応力度以下の応力度、
さらに曲げモーメントの場合では横座屈による低減された許容応力度以下の応力度内で部材サイズを選定する方法です。
応力度とは４つに大きく大別されます。
- 引張応力度
- 圧縮応力度
- 曲げ応力度
- せん断応力度
記号は[fb]で表し、bは”bending moment“の頭文字から来ています。単位は[N/mm2]です。
横座屈とは
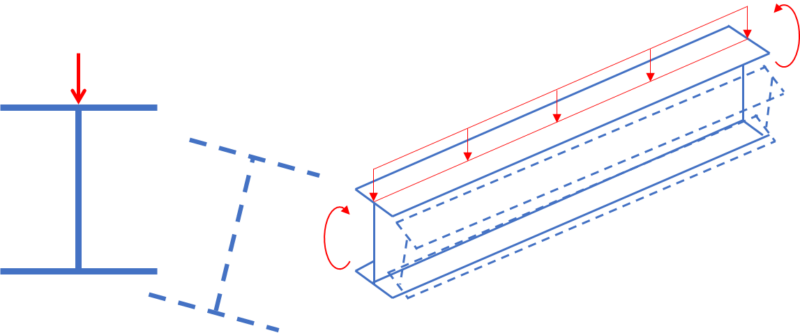
横座屈とは梁の強軸に曲げモーメントを受ける部材が軸対称から逸脱したねじりを伴った変形を弱軸に生じる座屈のことを指します。
横座屈を止める（生じさせない）ためには横補剛材やスチフナーをつけることで対策ができます。
横座屈はイメージしにくい座屈モードのなので見落としがちですが、非常に重要なトピックです。
鋼材の許容曲げ応力度は様々あり複雑です。一般的には旧規準式と2005年の新規準式があるので時と場合によって使い分けます。新規準式は手計算では追えないので旧規準式を使うことが多いです。
旧規準式の詳しい解説についてこちらの記事を参考にしてみて下さい！！
新規準(2005年)-許容曲げ応力度
新規準は旧規準に比べ、とても複雑です。サンブナンのねじりの式とワグナーのねじりの式の両方の式を考慮した式の構成となっています。
新規準式では大きく、a)～d) の4つに分類されます。分類されている意図は鋼材ごとに横座屈の有無や面外・面内などを明確に分ける必要があるからです。
新規準式は以下のようになります。
a)強軸周りに曲げを受ける材
強軸周りに曲げを受ける材(矩形中空断面を除く)の圧縮側許容曲げ応力度は以下の式のよる。
[許容曲げ応力度]
1. \(\lambda_{b}\leq {}_{p}\lambda_{b}\) のとき
\(f_{b}=\dfrac{F}{\nu}\) …（5.7式）
2. \({}_{p}\lambda_{b}\lt \lambda_{b}\leq {}_{e}\lambda_{b}\) のとき
\(f_{b}=\left(1-0.4\dfrac{\lambda_{b}-{}_{p}\lambda_{b}}{{}_{e}\lambda_{b}-{}_{p}\lambda_{b}}\right)\cdot \dfrac{F}{\nu}\) …（5.8式）
3. \({}_{e}\lambda_{b}\lt \lambda_{b}\) のとき
\(f_{b}=\dfrac{F}{2.17\cdot \lambda_{b}^2}\) …（5.9式）
λb:横座屈細長比
eλb:弾性限界細長比
pλb:塑性限界細長比
[安全率 ν]
\(\nu=\dfrac{3}{2}+\dfrac{2}{3}\left(\dfrac{\lambda_{b}}{{}_{e}\lambda_{b}}\right)^2\)
横座屈細長比
横座屈細長比は部材が持つ降伏モーメントと弾性横座屈モーメントの平方根から計算される値であり、許容曲げ応力度を算出する際に必要なパラメータで弾性限界細長比と塑性限界細長比との比較に使われます。
記号は[λb]で表し、単位は無次元です。計算式は以下になります。
[横座屈細長比]
\(\lambda_{b}=\sqrt{\dfrac{M_{y}}{M_{e}}}\)
[降伏モーメントMy]
\(M_{y}=F\cdot Z\)
[弾性横座屈モーメントMe]
\(M_{e}=C\sqrt{\dfrac{\pi^4 E^2 I_{Y}I_{W}}{l_{b}^4}+\dfrac{\pi^2 E I_{Y}GJ_{T}}{l_{b}^2}}\)
F:基準強度
Z:断面係数
C:曲げモーメント係数
E:ヤング係数
IY:弱軸周りの断面2次曲げモーメント
IW:曲げねじり定数
G:せん断弾性係数
JT:サンブナンのねじり定数
曲げモーメント係数
曲げモーメント係数は以下に示します。
\(C=1.75+1.05\left(\dfrac{M_{2}}{M_{1}}\right)+0.3\left(\dfrac{M_{2}}{M_{1}}\right)^2\)
ただし2.3以下
M1,M2：それぞれ座屈区間端部において小さいほうおよび大きいほうの強軸周りの曲げモーメント(M2/M1)は複曲率の場合は正、単曲率の場合は負とする。区間中間モーメントがM1より大きい場合にはC=1.0とする。
曲げモーメントの詳しい解説はこちらの記事を参考にしてみて下さい。
曲げねじり定数
曲げねじり定数は曲げねじりに抵抗するためのパラメータで、これもまた計算が複雑化しています。(特にみぞ形鋼が…)
記号は[Iw]で表し、単位は[mm6]です。計算式は各断面によって変わり、以下の式になります。
[H形鋼]
\(I_{W}=\dfrac{t_{f}B^3 h^2}{24}\)
[みぞ形鋼]
\(I_{W}=\dfrac{t_{f}B^3 h^2}{12}\cdot \dfrac{3t_{f}B+2}{6t_{f}B+t_{w}h}\)
\(h=H-2t_{f} \)
[等辺山形鋼]
\(I_{W}=\dfrac{(tb)^3}{18}\)
\(b=B-0.5t\)
サンブナンのねじり定数
サンブナンのねじり定数は純ねじりに抵抗するためのパラメータで、同じく計算が複雑化しています。
記号は[J]や[JT]で表し、単位は[mm4]です。計算式は各断面によって変わり、以下の式になります。
[H形鋼およびみぞ形鋼]
\(J_{T}=\dfrac{1}{3}\cdot\{2B{t_{f}}^3+(H-2t_{f}){t_{w}}^3\}\)
\(h=H-2t_{f} \)
[等辺山形鋼]
\(J_{T}=\dfrac{2}{3}bt^2\)
\(b=B-0.5t\)
弾性限界細長比
弾性限界細長比は圧縮応力度における限界細長比と同様に基準強度の60％で設定されている定数です。
主に許容曲げ応力度を算出する際に必要なパラメータで横座屈細長比との比較に使われます。
横座屈細長比が弾性限界細長比よりも小さい場合の座屈モードは弾性横座屈になります。
記号は[eλb]で表し、eは弾性を表すelasticの頭文字を使っています。
単位は無次元です。計算式は以下になります。
\({}_{e}\lambda_{b}=\dfrac{1}{\sqrt{0.6}}=1.29\)
塑性限界細長比
塑性限界細長比は許容曲げ応力度を算出する際に必要なパラメータで横座屈細長比との比較に使われます。
横座屈細長比が塑性限界細長比よりも小さくなると部材は横座屈現象を起こさなくなるので、(5.7)式からもわかるとおり、基準強度と安全率からのみで求まり、横座屈による低減は一切考慮されていません。
記号は[pλb]で表し、pは塑性を表すplasticの頭文字を使っています。
単位は無次元です。計算式は以下になります。
i) 補剛区間内で曲げモーメントが直線的に変化するとき
\({}_{p}\lambda_{b}=0.6+0.3\left(\dfrac{M_{1}}{M_{2}}\right)\)
ii) 補剛区間内で曲げモーメントが最大となるとき
\({}_{p}\lambda_{b}=0.3\)
M1,M2：それぞれ座屈区間端部において小さいほうおよび大きいほうの強軸周りの曲げモーメント(M2/M1)は複曲率の場合は正、単曲率の場合は負とする。
b) 円形鋼管、矩形中空断面材
円形鋼管、矩形中空断面材および荷重面内に対称軸を有し、弱軸まわりに曲げを受ける材ならびに面内に曲げを受けるガセットプレートの圧縮および引張側許容曲げ応力度はft(許容引張応力度)とする。
c) ベアリングプレートの許容曲げ応力度
ベアリングプレートなど面外に曲げを受ける板の許容曲げ応力度は（5.17）式の値とする。
\(f_{b1}=\dfrac{F}{1.3}\) …(5.17)式
F：基準強度 (N/mm2)
d) 曲げを受けるピンの許容曲げ応力度
ベアリングプレートなど面外に曲げを受ける板の許容曲げ応力度は（5.18）式の値とする。
\(f_{b2}=\dfrac{F}{1.1}\) …(5.18)式
F：基準強度 (N/mm2)
※ただしこの記事を書いている私自身も”曲げを受けるピン”が示す意味が分かりません。このような知恵袋の記事もありますが理解できませんでした。
ピンの意味するものがピン梁、ピン接合、ピンetc… 様々考えられ想像できません。もし意味を説明できる方がいればコメントいただけると幸いです。
許容曲げ応力度検定
許容応力度検定は許容応力度に対して部材の負担する応力度が上回らないかを検定することです。
構造設計では許容応力度分の応力度をよく検定比と呼びます。この検定比が1.0を上回らないことが許容応力度設計です。
[許容曲げ応力度検定]
\(\sigma_{b}<f_{b}\)
\(\dfrac{\sigma_{b}}{f_{b}}<1.0\)
σb：曲げ応力度 (N/mm2)
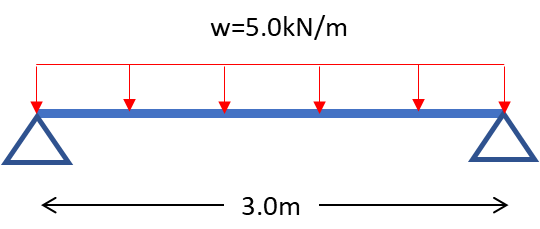
具体的な計算例を見ていきます。
梁材に等分布荷重w=5.0kN/mをかけたときの応力度検定をします。
柱材はH-100x100x6x8 部材長さ3.0ｍ(横補剛材なし) 弱軸周り断面2次モーメントIY＝134×104mm4 断面係数 Zx＝75.6cm3 材料をSS400材 ヤング係数E=205000N/mm2とします。簡易的な計算とするため自重は今回無視します。
まず部材に作用する曲げモーメントは
\(M=wl^2/8=5.0\cdot 3.0^2 / 8=5.63\)
つぎに部材に作用する曲げ応力度は
\(M/Z=5.63/ 75.6\cdot 1000=74.5\)
許容応力度fbを求めるためにまず横座屈細長比(降伏モーメントMy・弾性横座屈モーメントMe)を求めます。Cは単純梁なのでC=1.0になります。
\(My=F\cdot Z=235\cdot 74.5\cdot 10^3/1000^2=17.76kNm\)
曲げねじり定数とサンブナンねじり定数は
\(I_{W}=\dfrac{t_{f}b^3h^2}{24}=\dfrac{8*100^3*92^2}{24}=2.82*10^9\)
\(J_{T}=\dfrac{1}{3}\cdot\{2Bt_{f}^3+(H-2t_{f})t_{w}^3\}=\dfrac{1}{3}\cdot\{2*100*8^3+84*6^3\}=4.02*10^4\)
\(M_{e}=C\sqrt{\dfrac{\pi^4 E^2 I_{Y}I_{W}}{l_{b}^4}+\dfrac{\pi^2 E I_{Y}GJ_{T}}{l_{b}^2}}\)
$$M_{e}=1.0\sqrt{\dfrac{3.14^4 *205000^2 *134\cdot 10^4 *2.82\cdot 10^9}{3000^4}+\dfrac{3.14^2 *205000*134\cdot 10^4 *79000*4.02\cdot 10^4}{3000^2}}$$
\(M_{e}=33.88kNm\)
つまり横座屈細長比は
\(\lambda_{b}=\sqrt{\dfrac{17.76}{33.88}}=0.72\)
したがって\({}_{p}\lambda_{b}\lt \lambda_{b}\leq {}_{e}\lambda_{b}\) のとき\(0.3\lt 0.72\leq 1.29\) に該当することが分かりました。
（5.8式）で許容曲げ応力度を求めます。
\(\nu=\dfrac{3}{2}+\dfrac{2}{3}\left(\dfrac{\lambda_{b}}{{}_{e}\lambda_{b}}\right)^2\)
\(\nu=\dfrac{3}{2}+\dfrac{2}{3}\left(\dfrac{0.72}{1.29}\right)^2=1.71\)
\(f_{b}=\left(1-0.4\dfrac{\lambda_{b}-{}_{p}\lambda_{b}}{{}_{e}\lambda_{b}-{}_{p}\lambda_{b}}\right)\cdot \dfrac{F}{\nu}\)
\(f_{b}=\left(1-0.4\dfrac{0.72-0.3}{1.29-0.3}\right)\cdot \dfrac{235}{1.71}\)
\(f_{b}=114.1\)
\(\dfrac{\sigma_{b}}{f_{b}}=\dfrac{74.5}{114.4}=0.65\) …OK
以上よりこの梁材は許容応力度以内に納まっているので許容応力度設計では問題ないことが確認できました。このように部材の設計を行っていきます。
旧規準式でも同じ荷重を作用させた際の検討を行っていますが、この条件で計算した際は新規準の許容曲げ応力度＜旧規準式の許容曲げ応力度となり、旧規準式で検討すると危険側となります。
すべての条件においてこの不等式が成り立つわけではないので、設計者判断でどちらの規準式を適用させるか検討が必要です。
同じ計算条件で計算した旧規準式の記事はこちら
まとめ
今回は許容曲げ応力度についてまとめてみました。
許容応力度は構造設計をするうちで最も重要な値の一つです。この値を基準に部材サイズ・材質を決めたりしていきます。
一級建築士試験において許容曲げ応力度について問われることはほとんどありませんが、構造設計を生業とする場合は算出過程を頭の片隅ぐらいに覚えてください。新規準は計算がとても複雑で規準書を見ないで計算できる人はほぼいないと思います。ただ知っていると知らないのでは知識の差が大きく変わります。
鋼構造設計規準でも複雑化していることが普及につながらない、現在精査して式を刷新するとかしないとか書かれていました。
許容曲げ応力度を確認する場合は是非ともこの記事を読み直してみて下さい！！
コメント