今回は梁のたわみについてわかりやすく解説していきたいと思います
一級建築士試験における梁のたわみの問題は頻出問題で特に構造の計算問題として出題されています
予備校などでは係数の暗記になっていますが私もすぐに忘れてしまいます
試験本番でも忘れないように導出過程もあわせて覚えると確実に点が取れると思います
ぜひ参考にしてみて下さい
梁のたわみとは

たわみ(英:deflection)とは梁や床の水平部材に対してある一定の力が上からかけられると
梁や床は力と同じ向き(下方向)に沈みます
そのとき沈んだ距離のことをたわみと呼びます
たわみはどんなものにも起きます
気づいていないかもしれませんがあなたのいま乗っている床や地面
その他のなんであったとしても微小なりとも下向きに沈み、たわんでいます
記号は[δ]で表されることが多く
単位は[mm]や[cm]で表されることが多いです
梁のたわみの公式
梁のたわみの公式は端部の支持条件および荷重条件によって式が変わります
普遍的なことは常に分母に断面二次モーメントとヤング係数(弾性係数)があることです
この二つのパラメーターは断面二次モーメントとヤング係数は剛性(固さ)を表す数値で
たわみと反比例の関係にあります
よろしければ以下の記事を参考にしてみてください!
片持ち梁・集中荷重のたわみ
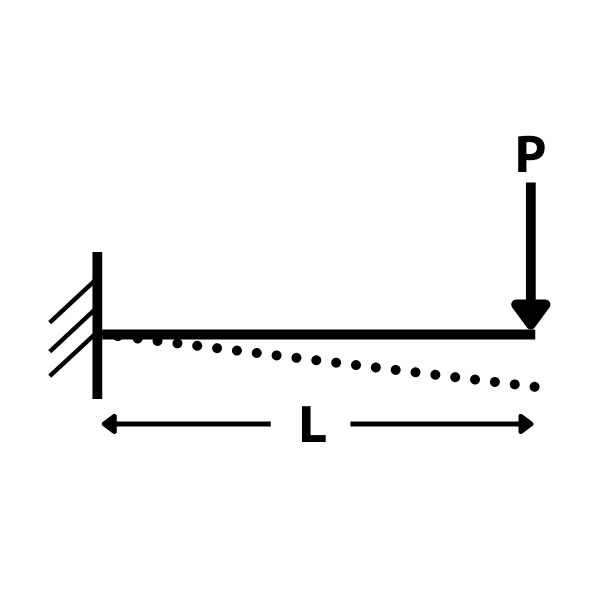
たわみ \(\displaystyle \delta=\frac{PL^3}{3EI}\)
たわみ角 \(\displaystyle \theta=\frac{PL^2}{2EI}\)
θ:たわみ角(自由端)
P:集中荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
詳しくはこちら
片持ち梁・等分布荷重のたわみ
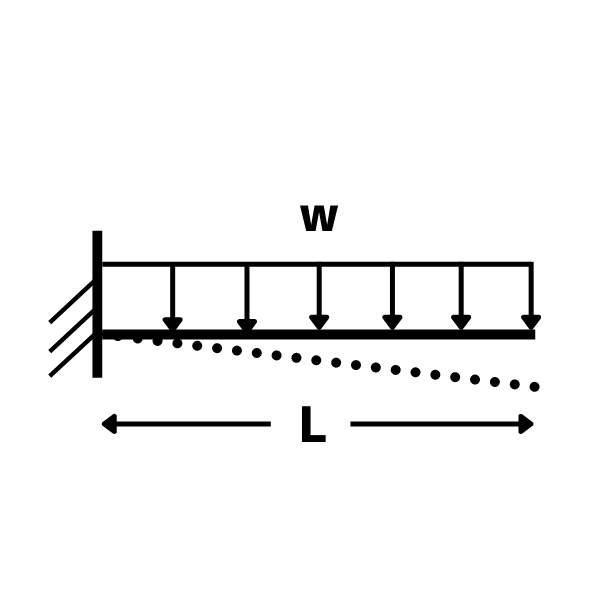
たわみ \(\displaystyle \delta=\frac{wL^4}{8EI}\)
たわみ角 \(\displaystyle \theta=\frac{wL^3}{6EI}\)
θ:たわみ角(自由端)
w:等分布荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
詳しくはこちら
単純梁・集中荷重のたわみ
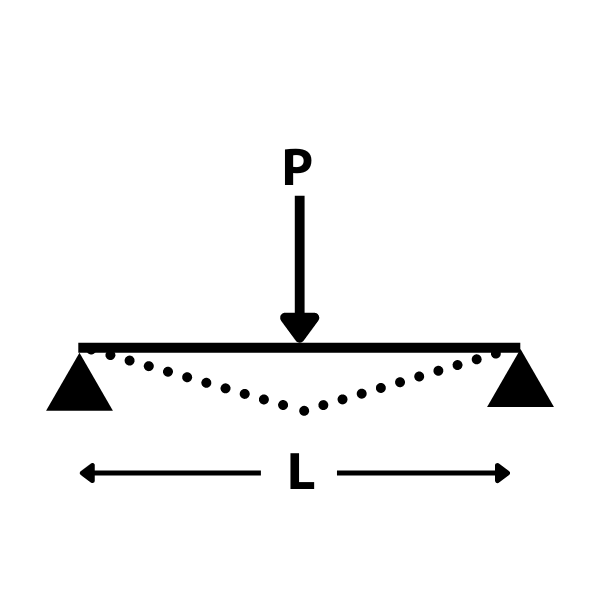
たわみ \(\displaystyle \delta=\frac{PL^3}{48EI}\)
たわみ角 \(\displaystyle \theta=\frac{PL^2}{16EI}\)
θ:たわみ角(支持点)
P:集中荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
詳しくはこちら
単純梁・等分布荷重のたわみ
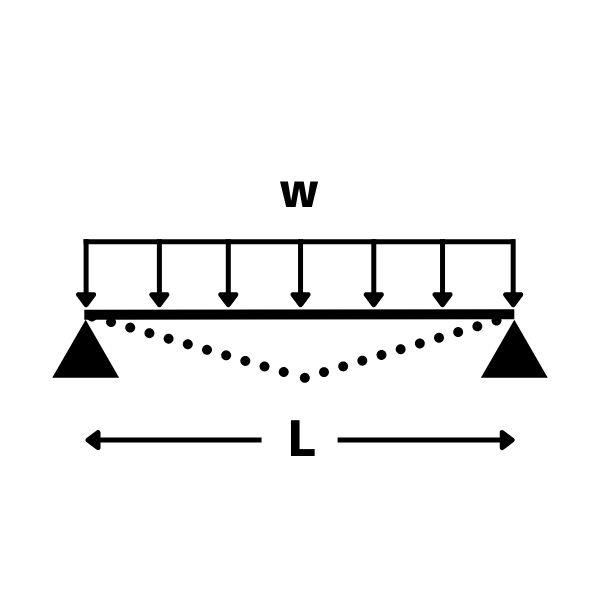
たわみ \(\displaystyle \delta=\frac{5wL^4}{384EI}\)
たわみ角 \(\displaystyle \theta=\frac{wL^3}{24EI}\)
θ:たわみ角(支持点)
w:等分布荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
詳しくはこちら
両端固定梁・集中荷重のたわみ
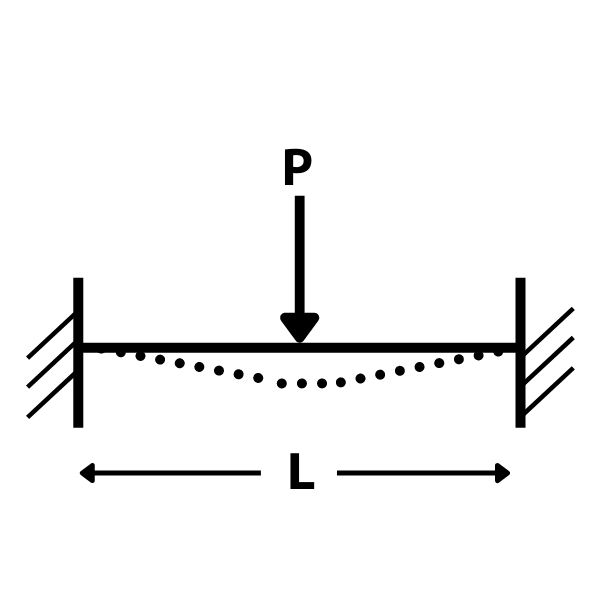
たわみ \(\displaystyle \delta=\frac{PL^3}{192EI}\)
P:集中荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
詳しくはこちら
両端固定梁・等分布荷重のたわみ
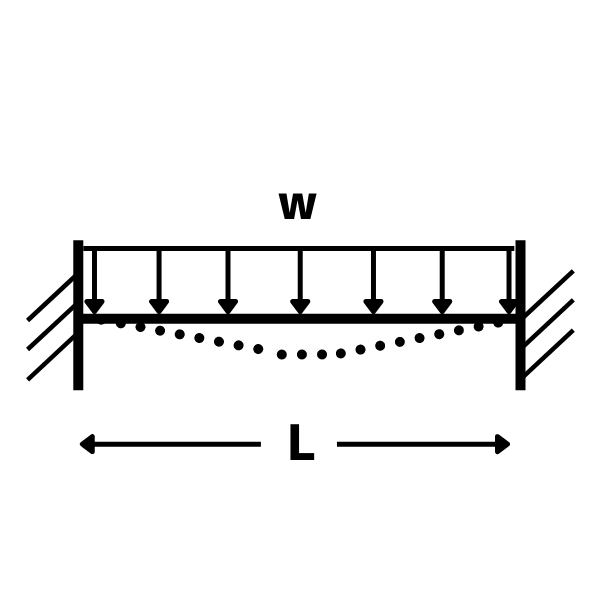
たわみ \(\displaystyle \delta=\frac{wL^4}{384EI}\)
w:等分布荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
詳しくはこちら
たわみの公式の覚え方
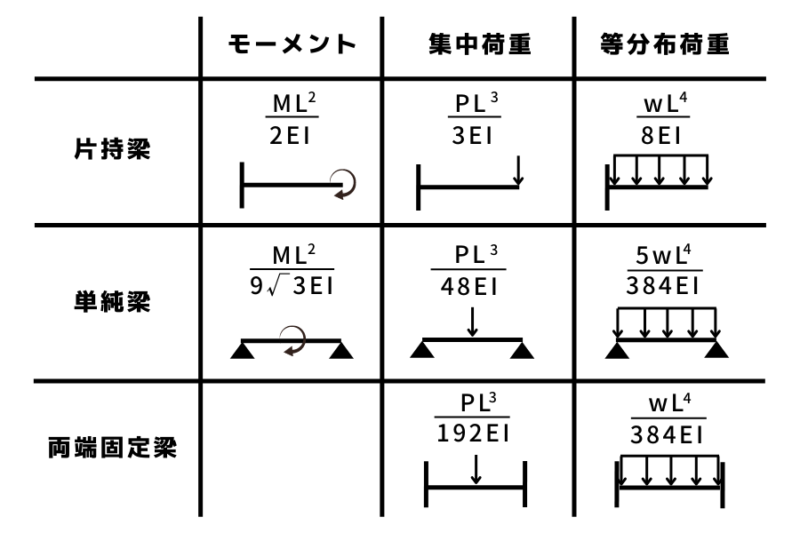
実際のテストでたわみの公式を思い出すときにはどのような覚え方が効率的かを考えると
まず荷重の種類によって長さLにかかる累乗の数に違いがあります
モーメント荷重 : \(\frac{ML^2}{EI}\)
集中荷重 : \(\frac{PL^3}{EI}\)
等分布荷重 : \(\frac{wL^4}{EI}\)
表で見ると右にずれるとLの累乗の数か増えるのに対し
縦にずれても(梁の固定条件が異なっても)Lの累乗の数は一定です
ぜひここは覚えてみてください
あとは式にかかる係数を覚えるだけです語呂合わせは
片持梁-モーメント 1/2 (に)
片持梁-集中荷重 1/3 (さん)
片持梁-等分布荷重 1/8 (ぱい)
単純梁-モーメント 1/9√3 (くるみ)
単純梁-集中荷重 1/48 (しっぱい)
単純梁-等分布荷重 5/384 (勇み足)
両端固定梁-集中荷重 1/192 (いいくに)
両端固定梁-等分布荷重 1/384 (さっぱし)
たわみの公式の係数を忘れたとき
たわみの公式の係数は覚えづらく
覚えたところでテストの点を取ること以外に意味がなくあまり本質的ではありません
しかしテストで忘れてしまった時のために導出の仕方は覚える必要があります
覚えるべきことは3つ
- たわみの曲線方程式\(\frac{d^2y}{dx^2}=-\frac{M(x)}{EI}\)を覚える
- モーメント\(M(x)\)の式を作る
- 境界条件を覚える
になります 一つひとつみていきましょう
1.たわみの曲線方程式を覚える
たわみの曲線方程式は\(\frac{d^2y}{dx^2}=-\frac{M(x)}{EI}\)です
ここで難しいと感じるのは\(\frac{d^2y}{dx^2}\)の部分だと思います
ただこれも深く考えずとても単純です
覚えるべきなのは
\(\frac{M(x)}{EI}\)の式を2回積分するとたわみの式になるということだけです
また\(\frac{M(x)}{EI}\)の式を1回積分するとたわみ角の式になります
EI(ヤング係数と断面二次モーメント)も最悪覚えなくても特に支障なく問題が解けてしますので
最後分母に付け加える程度でもいいです
2.モーメントM(x)の式を作る
\(M(x)\)の式はそれぞれの支持条件によって変化します
\(M(x)\)を求めるにはまず反力を求める必要があります
反力を求めたら反力の位置から\(x\)進んだところでのMの式を作ってみてください
それが\(M(x)\)の式になります
片持ち梁の集中荷重であれば
\(M(x)=P(x-L)\)
単純梁の等分布荷重であれば
\(M(x)=\dfrac{wL}{2}x−\dfrac{wx^2}{2}\)
のようなモーメントの式を作れるようになってください
3.境界条件を覚える
最後は境界条件を覚えることです
たわみの曲線方程式を積分していくうえで積分の都合上
積分定数が出てきますその積分定数を求める際に境界条件を用います
境界条件は
固定端ではたわみδ=0、たわみ角θ=0
ピン支点ではたわみδ=0
対称的な架構では中央のたわみ角θ=0
最低限これだけは覚えておきましょう!
具体的なたわみの問題例
最後に実際にあった一級建築士試験の問題からたわみを求めてみましょう
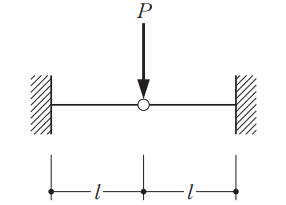
問題内容は省略しますがこのような普段見慣れない架構のたわみを求める問題でしたが
上記の手順でたわみを求めてみたいと思います
[計算過程]
まずモーメントの式M(x)を求めます
反力は対称なので荷重Pに対して両端の反力はP/2同じくモーメント反力はPl/2となります
したがって\(x\)進んだところでのM(x)の式は
\(M(x)=Px/2-Pl/2=\dfrac{P(x-l)}{2}\)
勘のいい人はここでこの問題は片持梁-集中荷重のPをP/2に置き換えた構造と
全く同じと気が付くかもしれません
続けてたわみの曲線方程式\(\frac{d^2y}{dx^2}=-\frac{M(x)}{EI}\)より
1回積分を行い、たわみ角を求め
\(\theta(x)=\dfrac{dy}{dx}=-\dfrac{P}{2EI}(\dfrac{x^2}{2}-lx)+c_{1}\)
c1の積分定数を求めるために固定端の境界条件\(x=0\)でたわみ角0を使います
\(\theta(0)=-\dfrac{P}{2EI}(0^2/2-l\cdot 0)+c_{1}=0\)
\(c_{1}=0\)
\(\theta(x)=-\dfrac{P}{2EI}(\dfrac{x^2}{2}-lx)\)
となります
さらに積分します
\(\delta(x)=\dfrac{d^2y}{dx^2}=-\dfrac{P}{2EI}(\dfrac{x^3}{6}-\dfrac{lx^2}{2})+c_{2}\)
c2の積分定数を求めるために固定端の境界条件\(x=0\)でたわみ0を使います
\(\delta(0)=-\dfrac{P}{2EI}(\dfrac{0^3}{6}-\dfrac{l\cdot 0^2}{2})+c_{2}=0\)
\(c_{2}=0\)
\(\delta(x)=-\dfrac{P}{2EI}(\dfrac{x^3}{6}-\dfrac{lx^2}{2})\)
したがって梁中央(\(x=l\))でのたわみは
\(\delta(l)=-\dfrac{P}{2EI}(\dfrac{l^3}{6}-\dfrac{l\cdot l^2}{2})\)
\(\delta(l)=\dfrac{l^3}{6EI}\)となり一級建築士試験の問題を解くことができました
構造の試験は時間が余ると思うのでぜひ解き方を覚えて暗記のミスをカバーしましょう!!
たわみ量の許容値
鋼構造設計規準ではたわみ量の許容値があります
通常(両端支持梁) : \(\displaystyle \frac{δ}{L}=\frac{1}{300}\)以下
片持ち梁 : \(\displaystyle \frac{δ}{L}=\frac{1}{250}\)以下
鉄骨の梁で設計する際はたわみの許容値1/300以下になるように設計しなければなりません
まとめ
今回はたわみ及びたわみ角についてまとめてきました
一級建築士試験でも頻出の問題です
予備校では暗記して覚えるよう教えられると思いますが
計算過程を合わせて覚えることで公式を暗記する必要はありません(計算の手間はかかりますが…)
必要なのはたったの3ステップ
たわみの曲線方程式の暗記・M(x)を作り方・境界条件を覚える
ただこれだけ覚えるだけで初見の問題でも解けると思います
しっかりこの記事を何度も見て勉強してください!!



コメント