今回は両端固定梁の集中荷重のたわみについてわかりやすく解説していきたいと思います
一級建築士試験のたわみの問題は係数の暗記になっていますがすぐに忘れてしまいます
導出過程もあわせて覚えると忘れてしまった場合でも試験で点が取れると思います
ぜひ参考にしてみて下さい
両端固定梁・集中荷重のたわみ
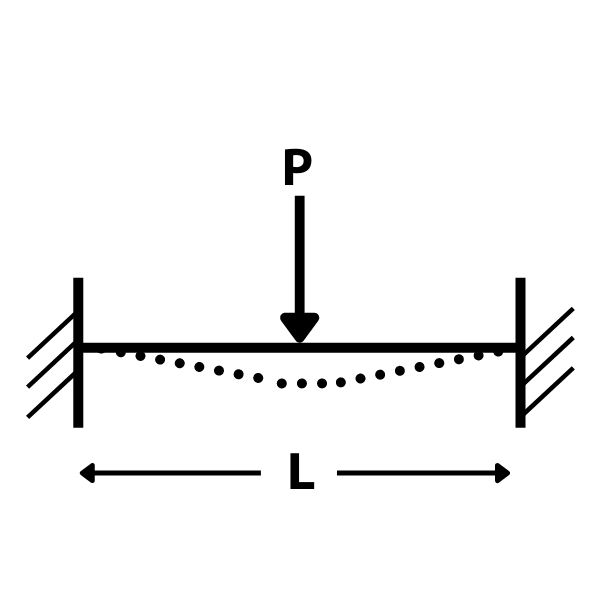
両端固定梁・集中荷重のたわみを式で表すと
\(\displaystyle \delta=\frac{PL^3}{192EI}\)
δ:たわみ(梁中央)
P:集中荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
両端固定梁・集中荷重のたわみ角
両端固定梁・集中荷重のたわみ角は端部および梁中央において
\(\displaystyle \theta=0\)
θ:たわみ角
両端固定梁・集中荷重のたわみの求め方
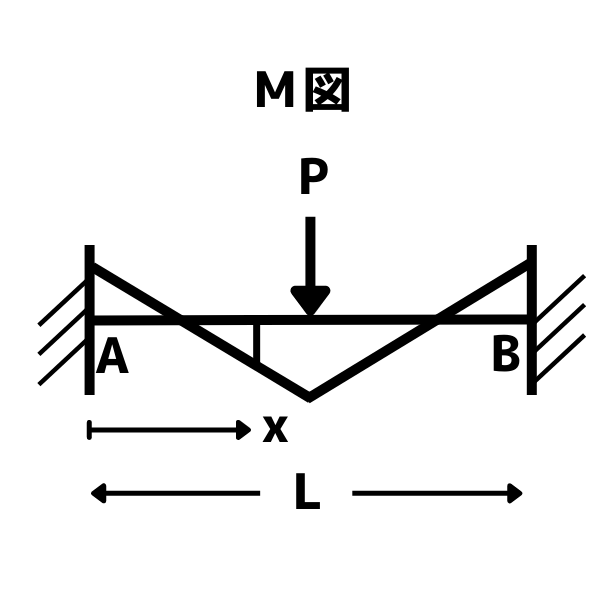
両端固定梁の集中荷重のたわみを求めるには
①支点の反力を求める
反力の大きさは荷重点の位置によって変わりますが今回のような梁中央に集中荷重がかかる場合は
A点・B点の反力は\(\frac{P}{2}\)
A点・B点のモーメント反力は\(Ma=-Mb\)とします
②M図を求める
両端固定梁の任意の点xにおけるモーメントは反力の大きさと距離xによって決まるので
M(x)の大きさを式で表すと
\begin{eqnarray}M(x)=\begin{cases}Px/2-M_{a}&(0\leq x\leq\frac{L}{2})
\\-P(x-L)/2-M_{a}&(\frac{L}{2}\leq x\leq L)\end{cases}\end{eqnarray}
③たわみ曲線の方程式に代入する
次にたわみ曲線の方程式\(\frac{d^2y}{dx^2}=-\frac{M}{EI}\)に先ほどのM(x)を代入すると
\(\displaystyle \frac{d^2y}{dx^2}=-\frac{Px/2-M_{a}}{EI}\)
シンプルに(0≦x≦L/2)の場合でのみ考えます
たわみの微分方程式を1回積分するとたわみ角、2回積分するとたわみになります
\(\displaystyle \theta(x)=\frac{dy}{dx}=-\int(\frac{Px/2-M_{a}}{EI})dx\)
\(\displaystyle \delta(x)=y=-\iint(\frac{Px/2-M_{a}}{EI})dxdx\)
④たわみ角の積分を解く
$$-\int(\frac{Px/2-M_{a}}{EI})dx=-\frac{Px^2}{4EI}+\frac{M_{a}x}{EI}+c_{1}$$
このとき積分定数c1を忘れないように
境界条件より\(x=0\)では\(\theta=0\)なので
\(\displaystyle c_{1}=0\) となり
\(\displaystyle \theta(x)=-\frac{Px^2}{4EI}+\frac{M_{a}x}{EI}\)
同じく境界条件より\(x=L/2\)でも\(\theta=0\)なのでモーメント反力\(M_{a}\)についても求まります
\(\theta(\frac{L}{2})=\displaystyle -\frac{P(\frac{L}{2})^2}{4EI}+\frac{M_{a}(\frac{L}{2})}{EI}=0\)
\(\displaystyle M_{a}=\frac{PL}{8}\)
上記をまとめるとたわみ角の式は
\(\displaystyle \theta(x)=-\frac{Px^2}{4EI}+\frac{PLx}{8EI}\)
⑤たわみの積分を解く
\(\displaystyle \delta(x)=\int (-\frac{Px^2}{4EI}+\frac{PLx}{8EI})dx\)
\(\displaystyle \delta(x)=-\frac{Px^3}{12EI}+\frac{PLx^2}{16EI}+c_{2}\)
このときも積分定数c2を忘れないように
境界条件より\(x=0\)では\(\delta=0\)なので
\(c_{2}=0\)となり
\(\displaystyle \delta(x)=-\frac{Px^3}{12EI}+\frac{PLx^2}{16EI}\)
たわみの最大となる\(x=L/2\)では
\(\delta(\frac{L}{2})=\displaystyle -\frac{P(\frac{L}{2})^3}{12EI}+\frac{P(\frac{L}{2})^2}{16EI}\)
\(\displaystyle \delta=\frac{PL^3}{192EI}\)となり公式の値と一致します
たわみ量の許容値
鋼構造設計規準ではたわみ量の許容値があります
通常(両端支持梁) : \(\displaystyle \frac{δ}{L}=\frac{1}{300}\)以下
片持ち梁 : \(\displaystyle \frac{δ}{L}=\frac{1}{250}\)以下
両端固定梁を鉄骨の梁で設計する際はたわみの許容値1/300以下になるように設計しなければなりません
具体的な計算例
最後に両端固定梁のたわみの計算とたわみが許容値以下に収まるか具体的な計算を見ていきます
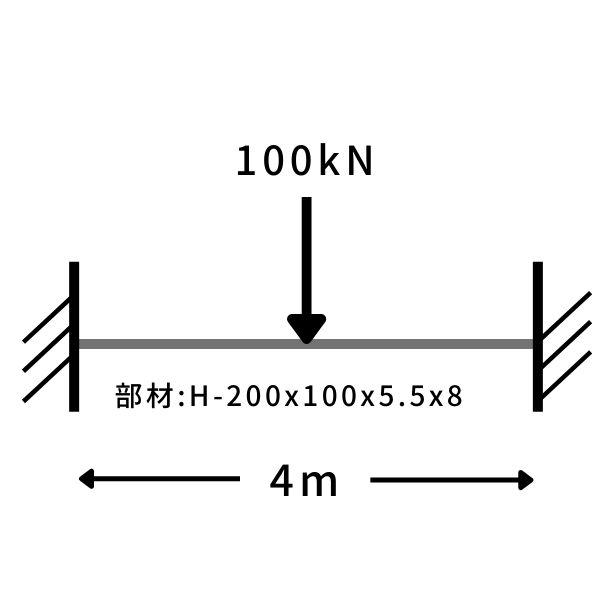
[設計条件]
部材:H-200x100x5.5×8 梁長さ:L=4m 弾性係数:E=205000N/mm2 断面二次モーメント:I=1810cm4
集中荷重:100kN
[計算過程]
たわみの公式より
\(\displaystyle \delta=\frac{PL^3}{192EI}\)
設計条件の値を代入し、たわみを求めると
\(\displaystyle \delta=\frac{100\times10^3\times4000^3}{192\times205000\times1810\times10^4}\)
\(=8.98\)mm
\(L/\delta=4000/8.98≒445\)
\(\displaystyle\frac{1}{445}<\frac{1}{300}\)
となり、たわみの許容値範囲内に収まり規準をクリアになることがわかりました
まとめ
今回は両端固定梁・集中荷重のたわみ及びたわみ角の計算方法についてまとめてきました
一級建築士試験でも頻出の問題です
予備校では暗記して覚えるよう教えられると思いますが計算過程を合わせて覚えることで公式を暗記する必要はありません(計算の手間はかかりますが…)
しっかりこの記事を何度も見て勉強してください!!



コメント
わかりやすい、有難うございます。
とても嬉しいです。励みになります、ありがとうございます。