今回は固有周期についてわかりやすく解説していきたいと思います。
一級建築士試験における固有周期の問題は水平剛性の問題と合わせて構造計算問題として出題されています。
試験本番でも忘れないように公式の導出過程もあわせて覚えると確実に点が取れると思いますのでぜひ参考にしてみて下さい。
固有周期とは
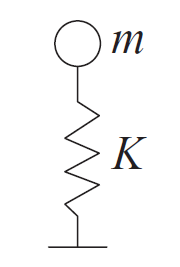
固有周期(英:natural period)とは建物などの物体の揺れが1往復するのにかかる時間を指します。
固有周期は質量や水平剛性、高さなどの要因によって決まります。
固有周期の記号は[T]つまり時間で表され、単位は[s]や[sec]の一秒単位で表します。式で表すと
固有周期 \(T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{K}}\)
K:ばね剛性
m:質量
ω:固有円振動数、角速度
固有周期の覚え方は
小学校で習った[時間]=[距離]÷[速度]を応用します。
ここで言う時間が固有周期に該当します。
つぎに距離は単位円を用います。単位円の半径を1とすると円周は\(2\pi\)になります。
つぎに速度は角速度ω[rad/s]です。
[時間]=[距離]÷[速度]を[固有周期]=[円周]÷[角速度]に変換し
\(T=\dfrac{2\pi}{\omega}\)
となります。
固有振動数とは
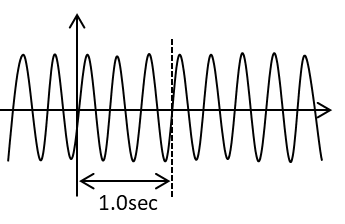
建築でいう固有振動数とは地震などの水平力を受けた層は水平方向に揺れます。このときに揺れが一秒間に往復する回数を指します。
固有振動数は固有周期の逆数です。
固有振動数の記号は[f]で表され、単位は[Hz]あるいは[1/sec] で表します。式で表すと
[固有振動数]
\(f=\dfrac{1}{T}=\dfrac{\omega}{2\pi}=\dfrac{1}{2\pi}\sqrt{\dfrac{K}{m}}\)
ω:固有円振動数
K:ばね剛性
m:質量
固有円振動数とは

建築でいう固有円振動数(英:circular frequency)とは円運動の角速度のことを指します。
たとえば単振動をする建物を例にとれば、最大振幅時には変位最大、加速度は0になり、振幅が0の状態では変位0、加速度が最大になります。
これは円周周りに速度ωで動く円運動に置き換えて考えるとイメージしやすいです。
固有円振動数の記号は[ω]で表され、単位は[rad/s]で表します。固有円振動数の式は
[固有円振動数]
\(\omega=\sqrt{\dfrac{K}{m}}\)
K:ばね剛性
m:質量
固有円振動数の導出
固有円振動数は『フックの法則』と『運動方程式』から導くことができます。
フックの法則は力はバネと変位で表すことができ、式は
\(F=K\delta\)
つぎに運動方程式は力は質量と加速度で表すことができ、式は
\(F=ma\)
上記の式を等式にすることで
\(K\delta-ma=0\)
ここで変位δを時間tでの変数として表し\(y(t)\)とし、また変位を時間tで2回微分すると加速度になるという法則を用い以下のように表します。
\(\delta=y(t)\)
\(a=\ddot{y}(t)\)
\(Ky(t)-m\ddot{y}(t)=0\) …(1)
つぎに微分しやすくするため\(y(t)=Acos\omega t\)とおきます。
ここでAを振幅、ωを角速度とします。
\(y(t)\)の微分\(\dot{y}(t)\)は
\(\dot{y}(t)=-A\omega\sin\omega t\)
さらに\(\dot{y}(t)\)の微分\(\ddot{y}(t)\)は
\(\ddot{y}(t)=-A\omega^2\cos\omega t\)
以上を(1)の式に代入し、
\(K(A\cos\omega t)-m(-A\omega^2\cos\omega t)=0\)
約分で消せるものを消し、シンプルにすると、
\(K-m(-\omega^2)=0\)
\(\omega=\sqrt{\dfrac{K}{m}}\)
以上のように導出することができました。
固有周期と水平剛性
実際の一級建築士の試験では固有周期と水平剛性をあわせた問題が出題されます。
固有周期や固有円振動数で用いたばね剛性Kを水平剛性に置き換えることで問題を解くことができます。
水平剛性については他の記事でまとめているのでぜひ参考にしてみてください。
水平剛性の公式
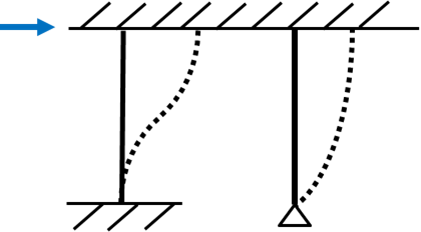
水平剛性の公式は
ピン支点-水平剛性 \(K=\dfrac{3EI}{L^3}\)
固定支点-水平剛性 \(K=\dfrac{12EI}{L^3}\)
E:ヤング係数
I:断面二次モーメント
L:部材長
水平剛性の式は端部の支点の条件によって式の係数が変わります。
分子に断面二次モーメントとヤング係数(弾性係数)、分母に長さの3乗は共通です。
ピン支点のほうが柔らかく、固定支点のほうが硬いので『ピンは3・固定は12』と覚えてしまいましょう。
固有周期の式のKを水平剛性の公式に置き換えると
ピン支点-固有周期 \(T=2\pi\sqrt{\dfrac{mL^3}{3EI}}\)
固定支点-固有周期 \(T=2\pi\sqrt{\dfrac{mL^3}{12EI}}\)
E:ヤング係数
I:断面二次モーメント
L:部材長
m:質量
具体的な問題
最後に実際にあった一級建築士試験の固有周期の問題から解いてみましょう
固有周期の問題
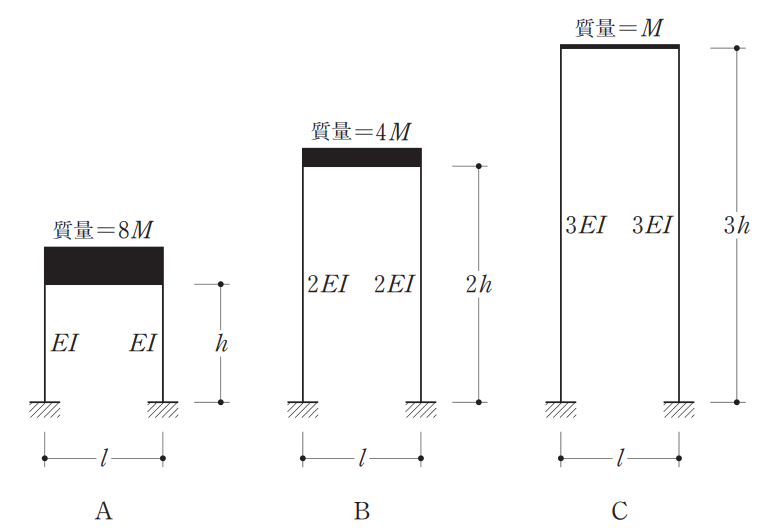
[問題]
それぞれのモデルA、B、Cの固有周期を求める問題で同じく水平剛性の知識も問われています。
ここでのポイントは「1質点系モデルに直す」ことつまり柱の水平剛性を合計します。
基本的に固有周期を求める問題は柱2本では解かずに1質点系モデルに直す必要があるので、柱1本の剛性のまま解いてしまうと間違えてしまうので注意してください!
[計算過程]
まずはそれぞれのモデルの水平剛性を求めます。
\(K_{A}=\dfrac{12*EI*2}{h^3}=\dfrac{24EI}{h^3}\)
\(K_{B}=\dfrac{12*2EI*2}{(2h)^3}=\dfrac{6EI}{h^3}\)
\(K_{C}=\dfrac{12*3EI*2}{(3h)^3}=\dfrac{8EI}{3h^3}\)
つぎに周期に直します
\(T_{A}=2\pi\sqrt{\dfrac{8M}{K_{A}}}=2\pi\sqrt{\dfrac{8Mh^3}{24EI}}\)
\(T_{B}=2\pi\sqrt{\dfrac{4M}{K_{B}}}=2\pi\sqrt{\dfrac{4Mh^3}{6EI}}\)
\(T_{C}=2\pi\sqrt{\dfrac{M}{K_{C}}}=2\pi\sqrt{\dfrac{3Mh^3}{8EI}}\)
あとはそれぞれ比べてみれば
\(T_{A}:T_{B}:T_{C}=\dfrac{1}{3}:\dfrac{2}{3}:\dfrac{3}{8}\)
答えは『TA:TB:TC=8:16:9』となります。
まとめ
今回は固有周期についてまとめてきました。あわせて固有振動数・固定円振動数についても触れました。
両方ともに一級建築士試験でも頻出の問題です。
固有円振動数ωのmとKどちらが分母・分子にくるか忘れてしまうかもしれませんが、フックの法則P=kδと運動方程式F=maから導出できます
この記事を何度も見て勉強してください!!それでは!!




コメント