水平剛性とは

今回は水平剛性についてわかりやすく解説していきたいと思います

一級建築士試験における水平剛性の問題は頻出問題で構造の計算問題として出題されています

試験本番でも忘れないように導出過程もあわせて覚えると確実に点が取れると思います

ぜひ参考にしてみて下さい

水平剛性とは

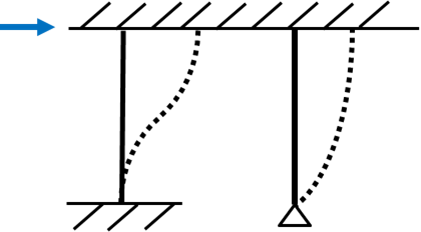
水平剛性(英:horizontal stiffness)とは梁や床をなしている層に対してある一定の力が水平方向（横）からかけられると、層は力と同じ向きに水平移動します。

水平の移動量に対して柱や壁は抵抗しようと逆向きにバネのような抵抗力がはたらきます。このときの水平方向の抵抗力を水平剛性あるいは柱や壁（鉛直部材）による水平方向の硬さとも言えます。

水平剛性は高層ビルなど縦に長い建物を例えるとイメージしやすいです。地震のような水平力を受け横に揺れたとき、水平剛性が大きいがっちりとした建物であれば揺れは小さく、水平剛性が小さいやわらかい建物であれば揺れは大きくなります。

建物や建築で言う水平剛性は耐震性とも言えます

水平剛性の記号は[ｋ]で表されることが多く、単位は[N/mm]や[kN/m]で表されることが多いです

水平剛性の特徴

水平剛性の特徴は単に水平剛性が大きければいいということでなく、剛性が大きくなるぶん、力を集中的に受けやすくなるので柱や壁にヒビや亀裂が多り損傷が多くなります

逆に水平剛性が小さいと部材がしなりやすく部材が損傷しにくくなる一方で、揺れは大きくなるので家具や中にいる人は横に大きく揺れるので被害が大きくなります

水平剛性の公式

水平剛性の公式はフックの法則から求めることができます

フックの法則（力＝バネ×変位）は

\(Q=k\cdot\delta\)

式変形することで上記の式を導くことができます

このときの水平変位δを片持梁-集中荷重のたわみの変位量δ=QL³/3EIに置き換えることで

Qとδを使わずに表現することでき、一級建築士試験では以下の式が多用されます

Qとδを用いない場合は端部の支点の条件によって式の係数が変わります

分子に断面二次モーメントとヤング係数(弾性係数)、分母に長さの3乗は共通です

ピン支点のほうが柔らかく、固定支点のほうが固いので

『ピンは３・固定は12』　とイメージすると覚えやすいのではないでしょうか！？

断面二次モーメントとヤング係数は剛性(固さ)を表す数値で水平剛性と比例、水平変位と反比例の関係にあります。よろしければ以下の記事を参考にしてみてください！

断面二次モーメントとは

ヤング係数・弾性係数とは

ピン支点の水平剛性の導出

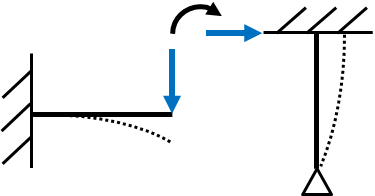
ピン支点の水平剛性の導出は片持梁-集中荷重のたわみより

図のように90°見方を変えるとわかりやすいかもしれません

一見すると荷重位置と支点の条件が違うように見えますがたわみは同じです

\(\delta=\dfrac{PL^3}{3EI}\)

\(P=k(\dfrac{PL^3}{3EI})\)

\(k=\dfrac{P}{(\frac{PL^3}{3EI})}=\dfrac{3EI}{L^3}\)

固定支点の水平剛性の導出

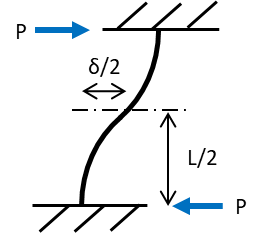
固定支点は両端固定梁モデルを２つの片持梁モデルに分けて考えていきます。水平力Pがかかった場合、柱にはPというせん断力が発生した場合を想定します。柱のせん断はどこを切ってもPです

しかし分割したモデルに生じるたわみは元のモデルの半分のδ/2であり、たわみが作用する地点の柱長さは半分のL/2なので、片持梁のたわみは

\(\delta=\dfrac{PL^3}{3EI}\)

1/2モデルの片持梁のたわみに変化させ

\(\delta\Rightarrow \delta/2 \,\ L\Rightarrow L/2\)に置き換え

\(\delta/2=\dfrac{P(\frac{L}{2})^3}{3EI}=\dfrac{PL^3}{24EI}\)

\(\delta=\dfrac{PL^3}{12EI}\)

フックの法則から

\(P=k(\frac{PL^3}{12EI})\)

\(k=\dfrac{P}{(\frac{PL^3}{12EI})}=\dfrac{12EI}{L^3}\)

具体的な水平剛性の問題

最後に実際にあった一級建築士試験の問題から水平剛性を求めてみましょう

水平剛性比の問題

問題内容は水平力Pが一様に作用する場合柱A,B,Cのせん断力を求める問題です(このとき梁は十分に剛とします)

ここでのキーワードは『力は剛性の大きいものに集まる』です

[計算過程]

キーワードのように剛性が高ければ力は集まるつまり、「力」は「せん断力」、「剛性」は「水平剛性」なので、水平剛性の比（左右の柱の剛性比）によって負担するせん断力が決まります

つまり柱の剛性が左右同じであれば負担するせん断力は同じになるので、柱Aと柱Cのせん断力は計算せずとも同じです…『Q_A=Q_C＝P/2』

中央のモデルは左の柱と右の柱の剛比は

左柱:右柱\(=\dfrac{3EI}{H^3}:\dfrac{12EI}{H^3}=1:4\)

左柱:右柱\(=1/5P:4/5P\)

したがって柱Bのせん断力はQ_B＝P/5　答えは『Q_B<Q_A=Q_C』となります

2層構造物の水平剛性問題

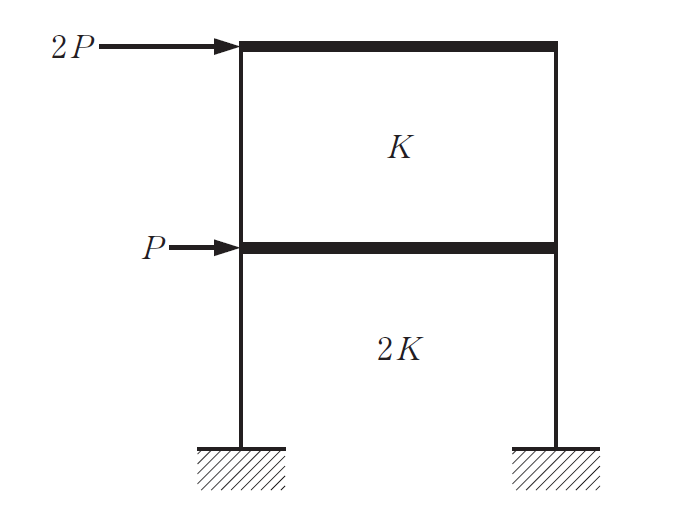
問題内容は図のような水平力が加わった場合の1層(2Fレベル)の水平変位と2層(屋上レベル)の水平変位の比を求める問題です(このとき梁は十分に剛とします)

解き方のキーワードは『当該層には上階からの水平力もかかる』です

[計算過程]

まずは2層(屋上レベル)の変位を考えます。水平剛性は柱2本でKという剛性を持ちます

フックの法則より2層のたわみδ₂は

\(\delta_{2}=\dfrac{2P}{K}\)

つぎに1層(2Fレベル)のたわみを求めます。上から来た水平力(せん断力)は柱を伝わって地面に流れていくので、キーワードのように当該層には上階からの水平力も加わり1層の水平力の合計は3Pになります。ここを理解していないと、この問題は解くことができません。

一方で水平剛性は上階の剛性の影響を受けない独立した数値ですので、柱2本で2Kという剛性を持ちます。同じようにフックの法則より1層のたわみδ₁は

\(\delta_{1}=\dfrac{3P}{2K}\)

両者の水平変位がそろい

答えは『δ₁:δ₂=3:4』となります。

この問題がたとえ3層や4層になったとしても『当該層には上階からの水平力も加わる』ことを忘れなければ、簡単に解くことができます！！

層間変形角の規定

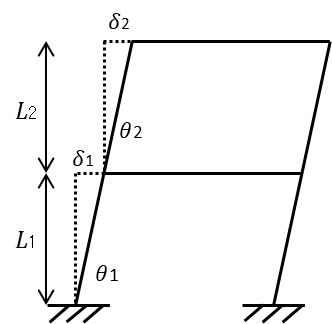
建築基準法では層間変形角に対して規定があります。

層間変形量とは柱長さ（階高）に対しての水平変位の比のことを指します

数式に表すと

建築基準法施行令 第82条の2 層間変形角　によると

建築物の地上部分については、第８８条第１項に規定する地震力（以下この款において「地震力」という。）によつて各階に生ずる水平方向の層間変位を国土交通大臣が定める方法により計算し、当該層間変位の当該各階の高さに対する割合（第８２条の６第二号イ及び第１０９条の２の２において「層間変形角」という。）が1/200（地震力による構造耐力上主要な部分の変形によつて建築物の部分に著しい損傷が生ずるおそれのない場合にあつては、1/120）以内であることを確かめなければならない。

建築基準法施行令 第82条の2

とあるので基本的に層間変形角を1/200を守る必要があります。もちろん様々な層間変形角を除外する規定もありますがここでは説明を省略します。

もし設計において層間変形角が1/200を超えた場合は、水平剛性つまり柱や壁の剛性を大きくするあるいは柱の長さを短くする必要があることを覚えておいて下さい！！

まとめ

今回は水平剛性についてまとめてきました。一級建築士試験でも頻出の問題で、重要な考え方のひとつです。

もし水平剛性の式を忘れてしまったら単純梁・集中荷重のたわみから導出できることをぜひ覚えて下さい

単純梁・集中荷重の公式も忘れてしまったら以下の記事で導出方法を覚えてみて下さい！！

記事を何度も見て勉強してください！！それでは！！