今回はせん断応力度についてまとめていきたいと思います
せん断応力は一級建築士試験でも出題される問題ですのでしっかり理解しましょう

せん断応力度ってなんだ??
せん断応力度とは
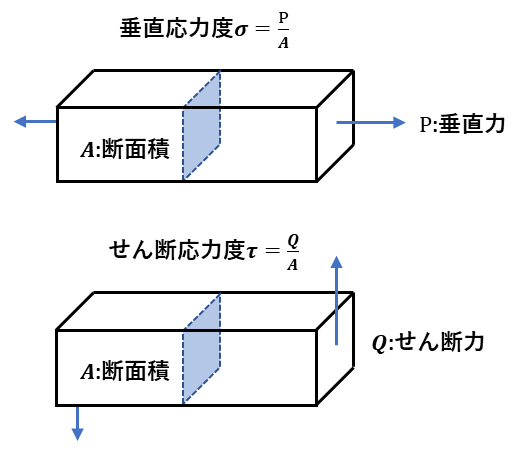
せん断応力度とは部材の断面積に対して直角に作用する力(せん断力)における単位面積当たりの力を指します。
逆に部材の断面積に対して垂直に作用する力(軸力)における単位面積当たりの力は垂直応力度(軸応力度)と言われています。
せん断応力度の記号は一般的に[τ]、単位は一般的に[N/mm2]で表します。
上記の図式は長方形断面のせん断力の算出に用いられますが、いろいろな形の部材断面があるので、いっしょくたんにせん断応力度を式で表すと
\(\tau=\dfrac{QS_{x}}{bI_{x}}\)
Q :せん断力
Sx :せん断応力度を算定する位置から最外縁までの部分のx軸に関する断面一次モーメント
b :断面の幅
Ix :x軸廻りの断面二次モーメント
せん断応力度の導出
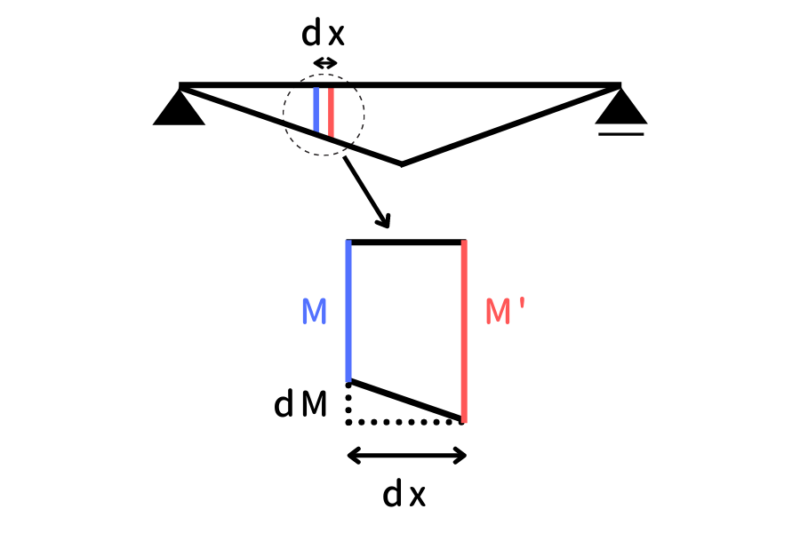
せん断応力度の導出にはまず曲げモーメント図の微小断面をピックアップします。ある点の曲げモーメントMとし、
そのときの部材の縁応力\(\sigma\)は(図の左の応力)
\(\sigma=\dfrac{M\cdot y}{I_{x}}\)
ある点からdx移動した点の曲げモーメントをM’とします。
M’はMよりもdM大きくなることからM’=M+dMとなり、
そのときの部材の縁応力\(\sigma+d\sigma\)は(図の右の応力)
\(\sigma+d\sigma=\dfrac{(M+dM)\cdot y}{I_{x}}\)
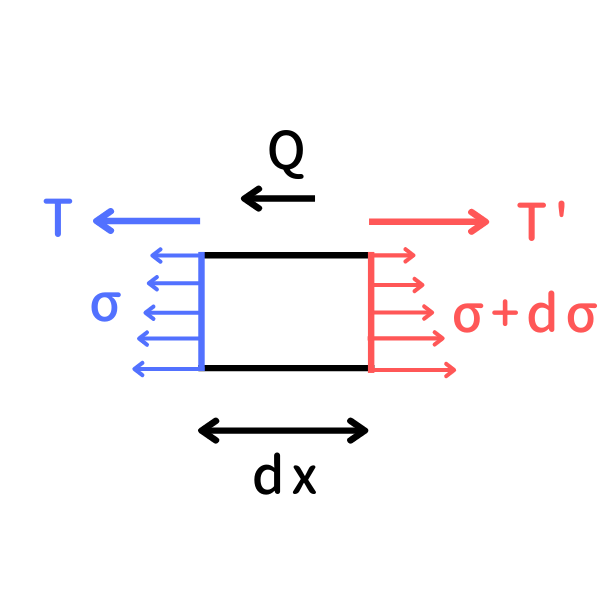
図のような曲げモーメントが生じるときは断面下端に引張応力が発生するので、
左側の引張応力\(T\)・右側の引張応力\(T’\)とします
\(T\)と\(T’\)には微小ながら左右の引張力に差が生じ(このときT’の方が大きい)
左右のつり合い条件を満たすためにdx間にはせん断応力Qが存在します
つまり式で表すと
\(T’ーT=Q\)
\(T\)および\(T’\)は引張応力度の面積和つまり積分で表すことができ
\(Q\)はせん断応力と作用する面積を除すことにより求めることができます
式に表すと
\begin{eqnarray}T&=&\int\sigma dA =\int\frac{M}{I_{x}}y\cdot dA\\
T’&=&\int (\sigma+d\sigma)dA=\int\frac{(M+dM)}{I_{x}}y\cdot dA\\
Q&=&\tau\cdot dx \cdot b\end{eqnarray}
上記の式をまとめると
\(\displaystyle \tau=\frac{1}{bI_{x}}\int\frac{dM}{dx} \cdot ydA\)
ここで
\(\dfrac{dM}{dx}=Q\)
\(\displaystyle \int ydA =S_{x}\)
Sxとは中立軸における断面一次モーメントを指します。
断面一次モーメントについては以下の記事を参考にしてください。
したがって
\(\tau=\dfrac{QS_{x}}{bI_{x}}\)
と導出することができました。
最大せん断力応力度とは
最大せん断力応力度とは断面のせん断力応力度の最大値のことを指します。
せん断応力度は断面内で大きさが変化します。
断面の縁は常に0となり重心に向かって放物線を描くように分布するのがせん断応力度の特徴です。
その放物線分布内で最大となる応力度を最大せん断力応力度といいます。
長方形の最大せん断力応力度
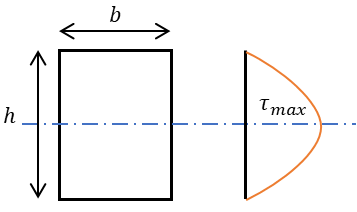
長方形断面の最大せん断力応力度は
\(\tau=\dfrac{3}{2}\cdot\dfrac{Q}{bh}\)
Q:せん断力
b:断面幅
h:断面せい
円の最大せん断力応力度

円形断面の最大せん断力応力度は
\(\tau=\dfrac{4}{3}\cdot\dfrac{Q}{\pi r^2}\)
Q:せん断力
r:半径
対称断面の最大せん断力応力度
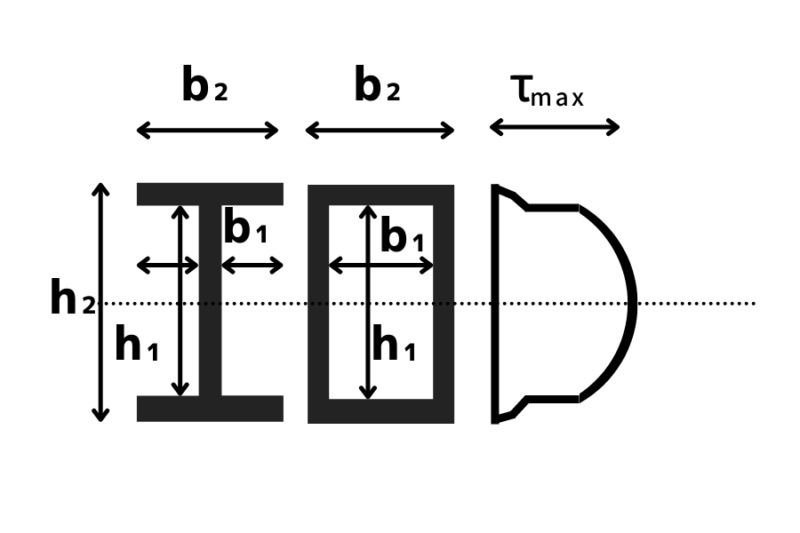
対称断面(H形鋼や角形鋼管あるいはチャンネル材)の最大せん断力応力度は
$$\tau=\dfrac{3Q}{2}\cdot \dfrac{b_{2}h_{2}^2-b_{1}h_{1}^2}{(b_{2}h_{2}^3-b_{1}h_{1}^3)(b_{2}-b_{1})}$$
Q:せん断力
b1:内法幅(断面幅-ウェブ厚)
b2:断面幅
h1:内法せい
h2:断面せい
例題:せん断応力度の算出
ここで最大せん断力応力度の算出法が分かったところで中立軸から任意点のyi におけるせん断応力度を求める例題をやってみましょう
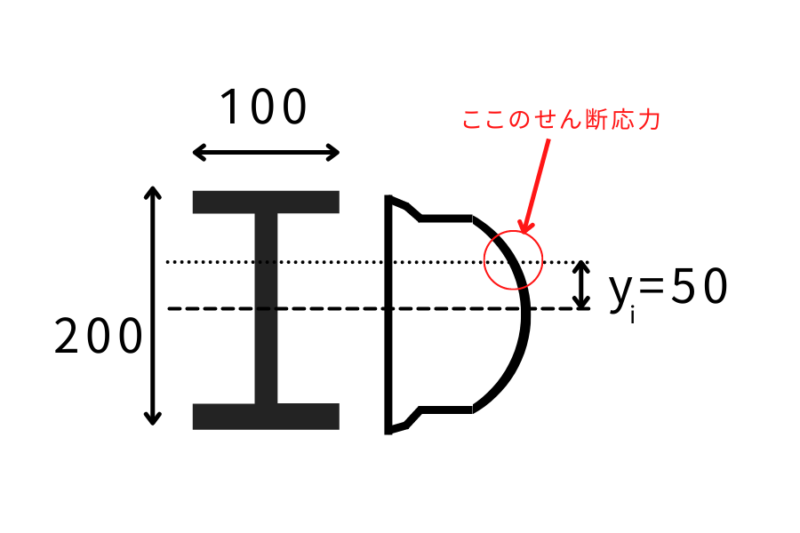
H形鋼H-200x100x5.5×8の中立軸からの距離yi=50mmのせん断力応力度を求める(フィレット部は考慮しない)
せん断力はQ=20kNとする
せん断応力度の公式より
\(\displaystyle \tau=\frac{QS_{x}}{bI_{x}}\)
なのでまず①断面二次モーメントIxを求めます
断面二次モーメントIxは
$$I_{x}=\frac{BD^3-(B-t_{w})(D-2t_{f})^3}{12}=17609322mm^4$$
次に②bを求めます
断面幅bは任意の点における幅になるので
\( b=t_{w}=5.5mm\)
最後に③断面一次モーメントSxを求めます
断面一次モーメントSxは
$$S_{x}=B\cdot t_{f} \cdot (D-t_{f})/2+t_{w} \cdot (D/2-t_{f}-y_{i}) \cdot [(D/2-t_{f}+y_{i})/2]$$
\(=93201mm^3\)
したがって任意点のせん断応力度は
\(\tau=\dfrac{20000×93201}{5.5×17609322}=19.25N/mm^2\)
このようにH形鋼の任意点であってもせん断応力度を求めることができます
断面一次モーメントの求め方はこちら
断面二次モーメントの求め方はこちら
平均せん断応力度とは
平均せん断応力度とは先ほど紹介した最大せん断力応力度の放物線分布の平均値になります。
単純にいえばせん断力を断面積で除した値になります。
記号は一般的に\(\tau_{ave}\)で表され、式で表すと
\(\tau_{ave}=\dfrac{Q}{A}\)
Q:せん断力
A:断面積
形状係数とは
せん断応力における形状係数とは平均せん断応力度に対する最大せん断力応力度の比です。
記号は一般的に\(\kappa\)で表され、式で表すと
\(\kappa=\dfrac{\tau_{max}}{\tau_{ave}}\)
形状係数は断面の形状が矩形や円形だった場合すぐに最大せん断力応力度を計算できる便利な値です
矩形の形状係数
\(\kappa=1.5\)
円形の形状係数
\(\kappa=\dfrac{4}{3}\)
円形中空管の形状係数
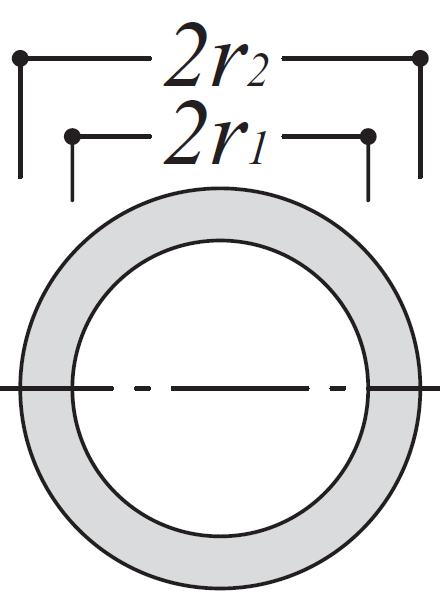
\(\kappa=\dfrac{4(r^2_{2}+r_{2}r_{1}+r_{1}^2)}{3(r_{2}^2+r_{1}^2)}\)
r1:内法半径 r2:外法半径
対称断面の形状係数
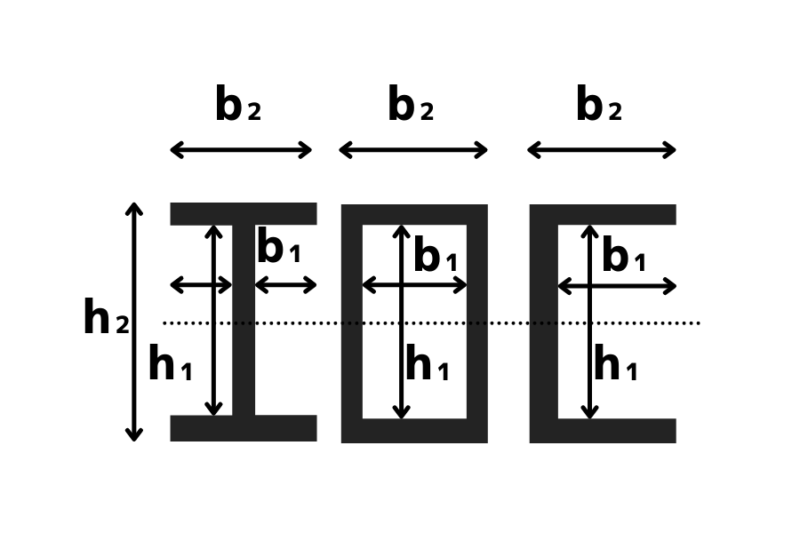
\(\kappa=\dfrac{3(b_{2}h_{2}^2-b_{1}h_{1}^2)(b_{2}h_{2}-b_{1}h_{1})}{2(b_{2}h_{2}^3-b_{1}h_{1}^3)(b_{2}-b_{1})}\)
b1:内法幅 b2:断面幅 h1:内法せい h2:断面せい
まとめ
今回はせん断応力度についてまとめてきました。
一級建築士試験でも出題されミスしやすい問題です。
最大せん断力応力度と平均せん断応力度は名前は似ていますが全く意味が異なります
せん断応力度は断面内であっても一様な応力度分布ではなく矩形ならば放物線のようにして中央で最大せん断力応力度となり
最大せん断力応力度は平均せん断応力度の1.5倍の大きくなるので注意しなければいけません!
せん断応力度は断面二次モーメント、断面幅および断面一次モーメントから求めることができます
以前紹介した断面一次モーメント・断面二次モーメントの記事と合わせて覚えて下さい!



コメント