今回は2020年度一級建築士 学科試験Ⅳ構造のNo.6の問題についてまとめていきたいと思います
今回は構造力学の座屈荷重の問題から出題されています。座屈荷重は公式と座屈長さ係数についての知識があれば解けると思いますが、今回は少しひねりが加えられておりやや難しい問題です
この記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

座屈荷重って!!どうやって解くの!?
問題 No.6
[No.6]
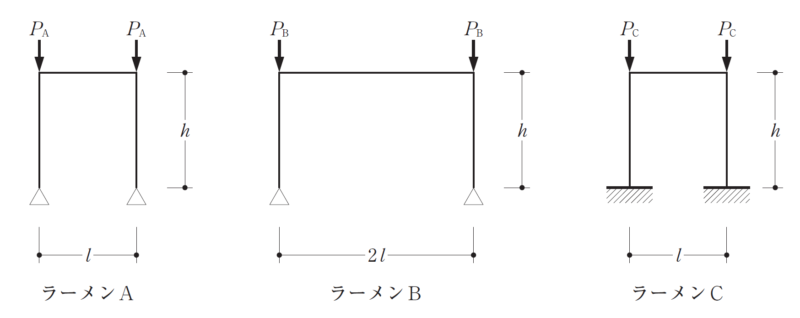
図のようなラーメンA、ラーメンB及びラーメンCの柱の弾性座屈荷重をそれぞれPA、PB及びPCとしたとき、これらの大小関係として、正しいものは、次のうちどれか。ただし、全ての柱及び梁は等質等断面の弾性部材であり、「柱及び梁の重量」及び「柱の面外方向の座屈及び梁の座屈」については無視するものとする。
[選択肢]
- PA=PC>PB
- PB>PA>PC
- PC>PA=PB
- PC>PA>PB
この問題キーワードは
- 座屈荷重の求め方
- 座屈長さ係数
- 梁が完全な剛体でないこと
になります。難しいことはないのでぜひ覚えてください
前提条件
この問題は以下の知識について問われています
- 座屈荷重
- 座屈長さ係数
ひとつずつ紐解いていきましょう!!
座屈荷重とは
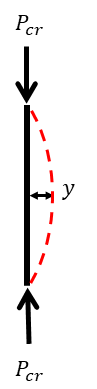
弾性座屈荷重(英:buckling load)とは軸方向に圧縮荷重を受ける一様断面の柱が弾性座屈を起こす荷重を指します。オイラー座屈(英:euler buckling)とも呼ばれます。
弾性座屈は細長い部材に圧縮を加えると部材が横にはらみ出る現象をいいます。逆に部材が太く短い部材であればあるほど弾性座屈は起きにくく、材料強度近くまで強度を発揮できます。
部材の座屈しにくさについては細長比で評価できるので詳しくはこちらの記事を参考にしてください→細長比とは
弾性座屈荷重の記号は[Pcr] で表現されます。単位は力の[kN]で表現されます。
式で表すと
[弾性座屈荷重]
\(P_{cr}=\dfrac{\pi^2 EI}{L_{k}^2}\)
E:ヤング係数(弾性係数)
I:断面二次モーメント
Lk:座屈長さ
式を見てわかることは、ヤング係数と断面二次モーメントは曲げ剛性を表すパラメーターであり、
ヤング係数は材料による硬さでマシュマロとコンクリートを数値的に表したものと同じで、
断面二次モーメントは断面の形状による硬さで断面積が大きいものと小さいものを数値的に表したもの
座屈長さは長いものと短いものに同じ圧縮力をかけたときにどちらが座屈しやすいかといえば、より長いものの方が座屈することはわかると思います。
これらを式で表現されているとわかります。詳しい解説は以下の記事を参考にしてください
座屈長さとは
座屈長さとは、ある支持条件に対して座屈する部分の長さです
記号では\(Lk\)で表現され、式で表すと
[座屈長さ]
\(L_{k}= K × L\)
K :座屈長さ係数
L :支点間距離
座屈長さ係数とは
座屈長さ係数は支持条件、境界条件によって値が変わります
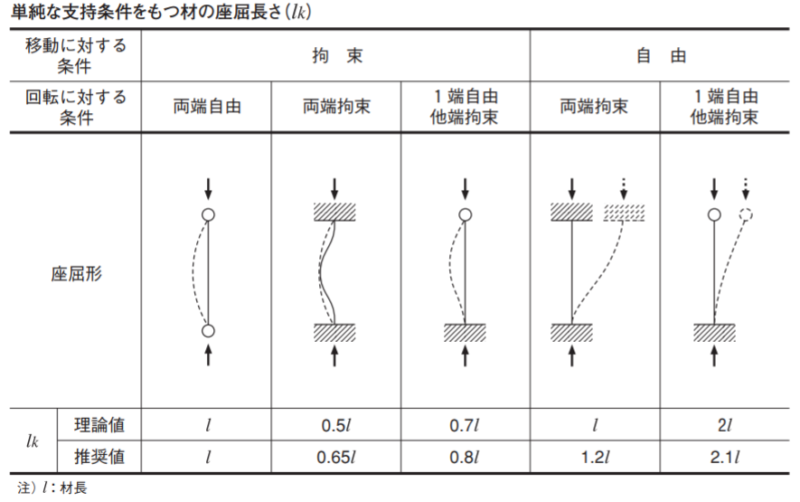
・移動に対する条件【拘束】
両端自由 K=1.0
両端拘束 K=0.5
一端自由 K=0.7
・移動に対する条件【自由】
両端拘束 K=1.0
一端拘束 K=2.0
移動に対する条件とは
ラーメン架構の柱は水平拘束なし→自由
ブレース架構の柱は水平拘束あり→拘束
回転に対する条件とは
柱端部の条件が剛接合であれば →拘束
柱端部の条件がピン接合であれば→自由
解き方
解く順序は
- 座屈長さ及び座屈長さ係数の算出
- 座屈荷重を求める
ひとつずつ算出していきましょう
1.座屈長さ及び座屈長さ係数の算出

まずは座屈長さ係数を算出しましょう。最初はラーメン形状が同じなラーメンAとラーメンCを比較します
ラーメン架構は水平移動に対して条件は自由で
支点の状態はラーメンAではピン、ラーメンCでは固定となるので、表で見るとここに該当します。
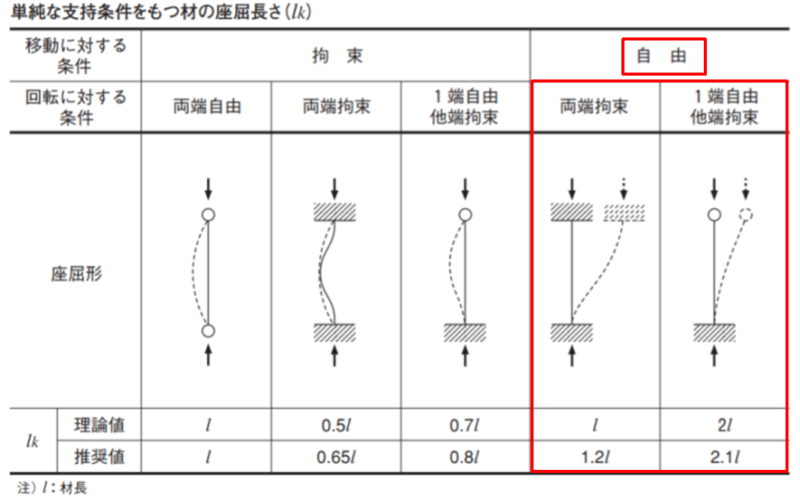
大小関係で座屈長さ係数を表すと
\(Kc>Ka\)
つぎに注目したいのがラーメンAとBの違いです。柱をつなぐ梁が完全な剛体でない(問題文に梁の剛体という記載がない)ため回転に対する条件が完全に拘束ではないということです。
拘束とピンとの境界線にある半拘束のような状態です。
『回転に対する条件が拘束に近くなると座屈長さ係数が小さくなり、回転に対する条件がピンに近くなると座屈長さ係数が大きくなる』という特性を覚えておく必要があります
話を元に戻しラーメンAとBの違いが梁の長さであることから
梁の長さが長いほど部材は剛性が下がり曲がりやすくなるつまり回転に対する条件が拘束が弱くピンに近くなり、梁の長さが短いほど部材しては曲がりにくくなるつまり回転に対する条件が拘束に近づく
つまりラーメンAの方が座屈長さ係数が小さく、ラーメンBの方が座屈長さ係数が大きくなることがわかり、数式で表現すると
\(Ka>Kb\)
以上をまとめると
\(Kc>Ka>Kb\)
座屈長さ\(L_{k}=K\times L\)に直すと
\(Lb>La>Lc\)
2.座屈荷重を求める
最後に座屈荷重を求めます。公式より
\(P_{cr}=\dfrac{\pi^2 EI}{L_{k}^2}\)
座屈長さの厳密な値は単純な計算からは求まりませんが、座屈長さの大小関係がわかっているので、座屈荷重の大小関係は
\(Pc>Pa>Pb\)
となり答えは④でした
まとめ
今回は2020年 一級建築士 学科試験Ⅳ構造 No.6の解説をしてきました
座屈荷重については座屈長さ係数の求め方がイマイチピンとこないので忘れてしまう人も多いかと思いますが、解き方のコツをちゃんと理解できれば簡単に解くことができます
詳しい解説を記事にしていますので、ぜひ座屈長さ係数の記事もあわせて是非参考にしてみて下さい!!




コメント