今回は2021年度二級建築士 学科試験Ⅲ建築構造のNo.1の問題についてまとめていきたいと思います
今回は材料力学の断面一次モーメントの問題から出題されています
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
問題 No.1
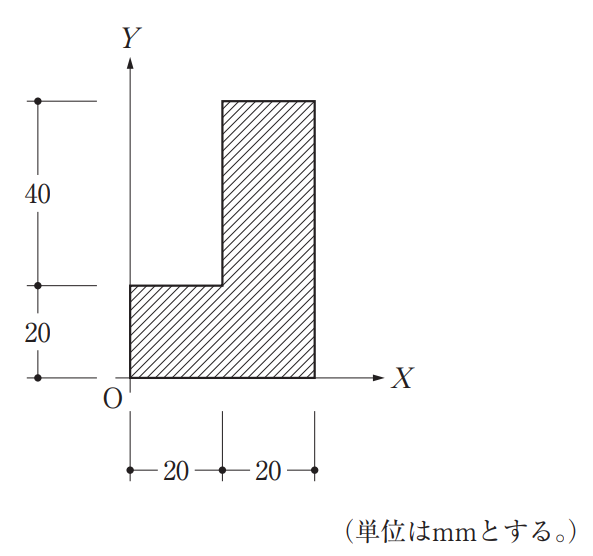
[No.1]
図のような断面において、図心の座標(x0,y0)の値として、正しいものは、次のうちどれか。ただし、x0= Sy/A 、y0= Sx/A であり、Sx、SyはそれぞれX軸、Y軸まわりの断面一次モーメント、Aは全断面積を示すものとする。
[選択肢]
1. x0=15 y0=35
2. x0=15 y0=25
3. x0=25 y0=15
4. x0=25 y0=25
5. x0=35 y0=15
この問題を解くためのキーワードは
- 断面一次モーメント
- 重心位置の求め方
前提条件
この問題は重心軸を探すためにまずは断面一次モーメントの公式、使い道を覚えておく必要があります
断面一次モーメント
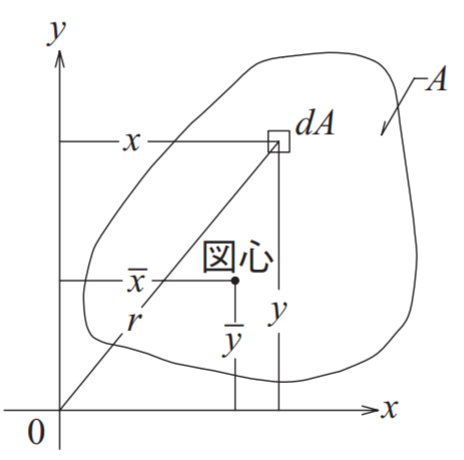
断面一次モーメントとは任意の軸から距離と微小面積dAの掛け合わせの合計値になります。一般的には重心軸を求める際に経由して使われるパラメーターです。
表記は[Sx],[Sy]あるいは[Gx],[Gy]で表すこともあります。単位は[cm3]で表記することが多いです
式で表すと
X軸周りの断面一次モーメント
\(S_{x}=\int ydA\)
Y軸周りの断面一次モーメント
\(S_{y}=\int xdA\)
y :任意の軸x0からの距離
x :任意の軸y0からの距離
dA:微小面積要素
しかしながら断面一次モーメント単体で使うことはめったにないです。
重心軸を求める際に一次モーメントの計算を経由して求めるため、問題にもあるように以下の式がより重要になります
\(y_{0}=\dfrac{S_{x}}{A}\ ,\ x_{0}=\dfrac{S_{y}}{A}\)
Sx Sy :X軸,Y軸周りの断面一次モーメント
y0 :Y座標の重心軸
x0 :X座標の重心軸
A :断面積
詳しい断面一次モーメント、重心軸の求め方についてはこちらの記事も参考にしてみて下さい!
解き方
解く方法順序は
- 断面を長方形2つに分割する
- 断面一次モーメントの計算
- 重心軸の算定
ひとつずつ算出していきましょう
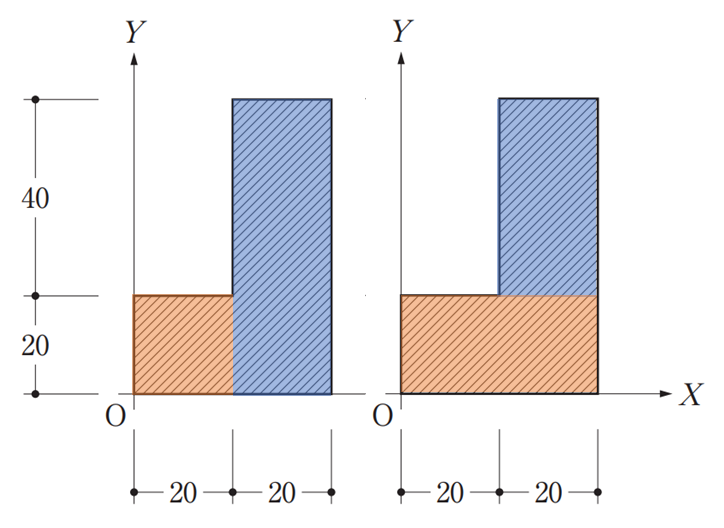
まず問題の図形が長方形ではなく複雑な図形なため断面が長方形になるように分割します。(より複雑な断面であっても図形をすべて円形・長方形に分けて考えましょう!)
上の図でもあるように分け方は2種類考えられます。どちらも正解ですが今回は右でトライしてみます。
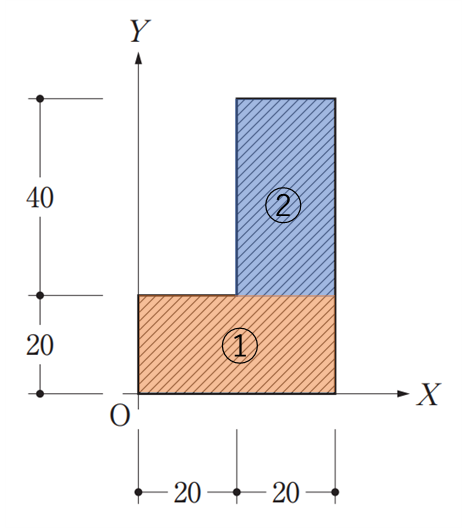
つぎに断面一次モーメントの計算をしていきます。今回必要となるのはy軸とx軸に関してなので同時に解いていきましょう。
長方形断面の断面一次モーメントの公式は\(S_{y}=y\cdot A\)なので
このときyを基準軸Yからの距離、xを基準軸Xからの距離、Aを断面積とします
①断面ーx軸
\(S_{x1}=10\cdot 40\times 20=8000\)
①断面ーy軸
\(S_{y1}=20\cdot 40\times 20=16000\)
②断面ーx軸
\(S_{x2}=40\cdot 20\times 40=32000\)
②断面ーy軸
\(S_{y2}=30\cdot 20\times 40=24000\)
最後に重心軸の算定していきます。先ほど求めた各長方形・軸周りの断面一次モーメントに断面積を除して計算していきます。このときにそれぞれの断面一次モーメントを合計し、断面を合計してから計算します。式で表すと
\(x_{0}=\dfrac{\Sigma S_{x}}{\Sigma A}=\dfrac{S_{x1}+S_{x2}}{A_{1}+A_{2}}\)
\(=\dfrac{8000+32000}{800+800}=25\)
\(y_{0}=\dfrac{\Sigma S_{y}}{\Sigma A}=\dfrac{S_{y1}+S_{y2}}{A_{1}+A_{2}}\)
\(=\dfrac{16000+24000}{800+800}=25\)
したがってまとめると『x0=25mm, yo=25mm』となり、最終的な答えは④でした
まとめ
今回は2021年 二級建築士 学科試験Ⅲ建築構造 No.1の解説をしてきました。
今回の問題は断面一次モーメントを利用する重心位置の算定です。断面一次モーメントを知らなくとも重心位置の算定のしかたを知っている方も多いかと思います。建築構造の分野でも基本的な問題で正答率もかなり高いと思われるので、もし忘れてしまった方は是非とも解けるようにしてください!!
断面一次モーメントの記事もあわせて参考にしてみて下さい
・断面が長方形ではなく円形になった場合
・断面の分割数が3つ以上になる場合
こちらも自分で問題を作って解いてみるとよいでしょう!!




コメント