今回は2021年度二級建築士 学科試験Ⅲ建築構造のNo.4の問題についてまとめていきたいと思います
今回は構造力学のトラス構造の問題から出題されています
力学の基本的な問題なのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
問題 No.4
[No.4]
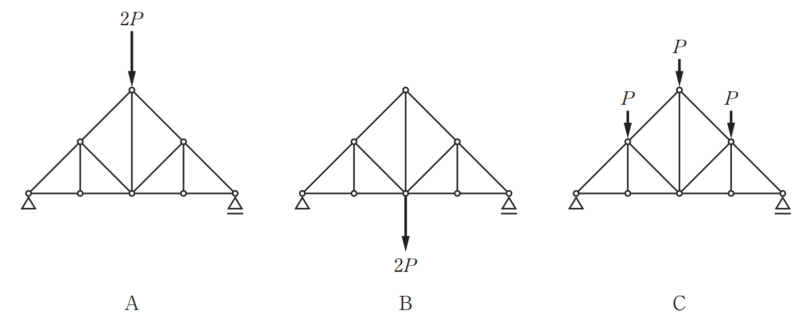
図のような、荷重条件が異なる静定トラスA、B、Cにおいて、軸方向力が生じない部材の本数の組合せとして、正しいものは、次のうちどれか。ただし、荷重条件以外の条件は、同一であるものとする。
[選択肢] A:B:C
- 3:3:3
- 4:3:1
- 4:4:2
- 5:4:2
- 5:5:5
この問題を解くためのキーワードは「節点法」です。力学の基本的な知識が問われています。

「トラス構造」「節点法」ってなんだっけ??
ひとつずつわかりやすく解説していきます!
前提条件
この問題を解くためには「トラス構造」および「節点法」さらには「節点法の重要な法則」について覚えておく必要があります。
トラス構造とは

トラス構造とは部材を三角形につなぎ合わせた構造形式で部材の節点はピン接合のものを指します。
トラスは軸力しか負担せず、曲げ・せん断力は、働かないものとします。
軸力とは引張力および圧縮力のことを指します。
数字上ではトラスの軸力が引張・圧縮どちらなのか判断がつかなくなるので通例的に
- 引張力を正(プラス)
- 圧縮力を負(マイナス)
として表現します、もちろん逆に考えても支障はありません
つり合い式をたてるときに軸力の向きは

- 節点を引くような向きを引張力
- 節点を押し込むような向きを圧縮力
と仮定します。
節点法とは
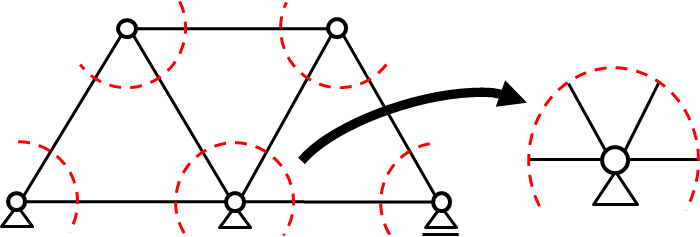
節点法とは支点における反力を求めた後、支点から出発し順次隣接の節点で力のつり合い式を立てて軸力を求めていく方法を指します。
節点法のメリットは、力のつり合い式のみから軸力を計算することができるので非常にシンプルな点です
節点法のデメリットは、節点に集まる力の未知数が3コ以上になると解くことが不可能になります
節点法の解き方
節点法の解き方は
- 支点反力をもとめる
- 反力点や未知数が2つ以下の節点にはたらくの力のつり合いをもとめる
- 2で解いた節点に隣合う未知数が2つ以下の節点の力のつり合いをもとめる
- 3の繰り返し
詳しい節点法の解説は以下の記事を参考にしてみて下さい
節点を直線につなぐトラス構造の法則
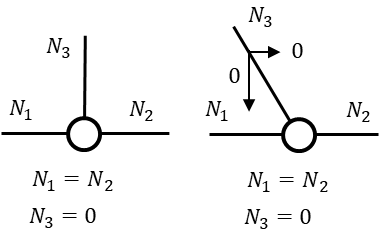
節点を直線につなぐトラス構造には法則があります。この法則をつかう条件は
- 2つの部材が直線上に接続されていること
- 節点に接続する部材数は3つであること
- 節点には荷重(外力)が作用しないこと
上記の図の場合でみると直線上の2つの部材の軸力(引張・圧縮力)は力のつり合い式によって常につり合うため
\(N_{1}=N_{2}\)
対して直角方向(図の場合は鉛直方向)の力が0でないと、力のつり合い式が成立しないため\(N_{3}\)の軸力は必ず0になります。(斜めに取りつく場合も0)
\(N_{3}=0\)
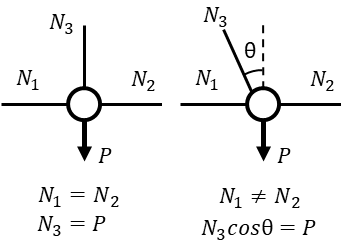
①節点には荷重(外力)が作用する場合かつ②3つ目の部材が直角に取りつく場合は
直線上の部材の軸力(引張・圧縮力)は常につり合い、直角方向(図は鉛直方向)の力がPでないと力のつり合い式が成り立たないため\(N_{3}\)(直線上にない部材)の軸力は常に荷重Pと一致します。
\(N_{1}=N_{2}\)
\(N_{3}=P\)
3つ目の部材が斜めに取りつく場合は直角方向の力がPになるように力のつり合い式を求めると
\(N_{3}\cos\theta=P\)
一方で\(N_{3}\)の水平成分の力が発生することにより
\(N_{1}≠N_{2}\)
となるので注意しましょう!
解き方
解く方法順序は
- 節点を直線につなぐトラス構造には法則を使う
のみです。ここまで長々と説明してきましたが今回紹介した知識のみで問題を解くことができます。
またこの問題のいやらしい点は『長さのパラメータ』が一切与えられていない点です。詳しくみてみましょう!
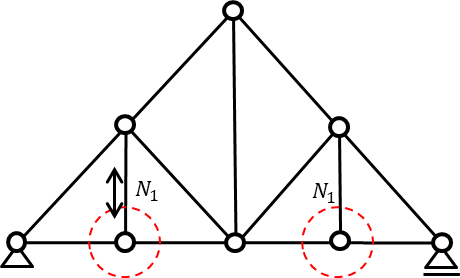
1つ目は左右から2番目の節点に注目します。先ほど紹介した節点を直線につなぐトラス構造の法則により鉛直方向へ伸びる部材軸力を\(N_{1}\)とすると、すべてのモデルA・B・Cで
\(N_{1}=0\) となります。
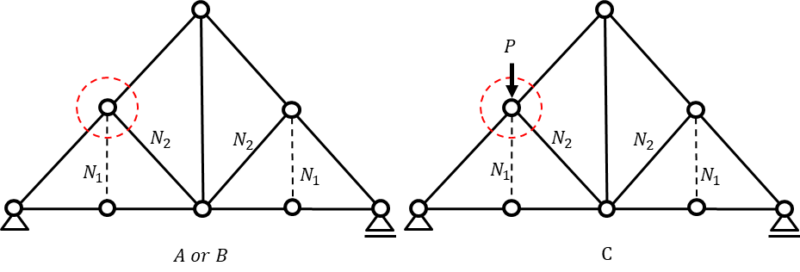
つぎは上から2番目の節点に注目します。
先ほど節点に接続する部材数は3つである必要があると説明し、注目する節点には部材が4つ接続されており法則が成立しないように見えますが、
\(N_{1}\)の軸力が0であるため、\(N_{1}\)を実質ないものとして扱い、節点を直線につなぐトラス構造の法則を適用します。
直角に取りつく部材軸力を\(N_{2}\)とすると、モデルA・Bは
\(N_{2}=0\)
モデルCにおいては節点に荷重が作用し\(N_{2}\)の直線上荷重が作用していないため
\(N_{2}≠0\)
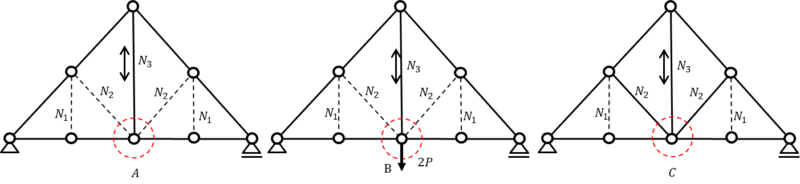
最後に中央部下の節点に注目します。
先ほどと同様に解くことができるのでモデルA・Bは\(N_{2}\)の軸力が0であるため、\(N_{2}\)を実質ないものとして扱い、節点を直線につなぐトラス構造の法則を適用します。
中央の部材軸力を\(N_{3}\)とすると
モデルA \(N_{3}=0\)
モデルBの節点に荷重が作用しているので
モデルB \(N_{3}=2P\)
モデルCの節点に接続する部材数は5つになるので
モデルC \(N_{3}≠0\)
まとめると
モデルA:\(N_{1}=N_{2}=N_{3}=0\) 5つの部材で軸力0
モデルB:\(N_{1}=N_{2}=0\) 4つの部材で軸力0
モデルC:\(N_{1}=0\) 2つの部材で軸力0
したがって答えは④の「5:4:2」でした
まとめ
今回は2021年 二級建築士 学科試験Ⅲ建築構造 No.4の解説をしてきました。
今回の問題はトラス構造で節点法や切断法で解いてしまったかもしれませんが、難しいところが『長さ』が一切与えられていません。したがって実質モーメントのつり合いで解くことができませんでした。
しかしながら『節点を直線につなぐトラス構造の法則』を知っていれば計算することもなく、簡単に解くことができます。今後は是非とも解けるようにしてください!!




コメント