今回は2022年度一級建築士 学科試験Ⅳ構造のNo.3の問題についてまとめていきたいと思います。
今回は力のつり合いの問題から出題されています。
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

力のつり合いの計算方法ってどうやるんだっけ!?
問題 No.3
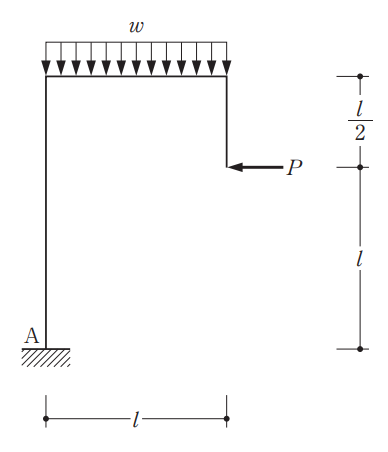
図のような鉛直方向に等分布荷重wと水平方向に集中荷重Pが作用する骨組において、固定端A点に曲げモーメントが生じない場合の荷重wlと荷重Pの比として、正しいものは、次のうちどれか。ただし、全ての部材は弾性部材とし、自重は無視する。
- \(wl:P=1:1\)
- \(wl:P=1:2\)
- \(wl:P=2:1\)
- \(wl:P=3:1\)
この問題キーワードは
- モーメントの計算
の一点のみですここだけ押さえておけばこの問題は簡単です。
前提条件
この問題はまずモーメントの計算と等分布荷重の計算のしかたについて理解する必要があります。
モーメントの計算方法
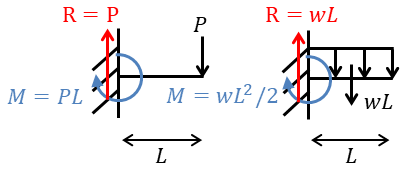
モーメントの計算方法は基本的に(固定端からの距離)×(力)で求まります。
集中荷重Pの固定端モーメントは
\(M=P\times L\)
等分布荷重wの固定端モーメントはまず等分布荷重wを集中荷重P=wLに変換して等分布荷重の重心位置の距離を固定端からの距離とします。したがって以下の式のようになります。
\(M=\dfrac{w\times L^2}{2}\)
以下は参考記事になります。是非ご覧になってください。
解き方
今回の問題の解く順序は
- 集中荷重によるの固定端曲げモーメントを算出する
- 等分布荷重によるの固定端曲げモーメントを算出する
- 2つ式を等式とし比率を出す
ひとつずつ算出していきましょう。
まずは集中荷重によるの固定端曲げモーメントを算出していきます。
集中荷重Pの固定端モーメントは\(M=P\times L\)で計算し
\(M=P\times l\)
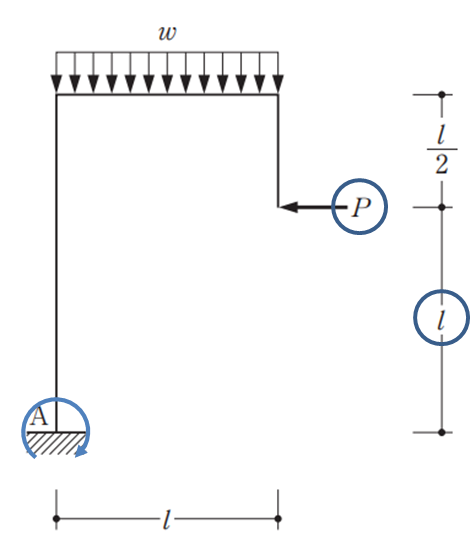
次に等分布荷重wによるの固定端曲げモーメントを算出していきます。
等分布荷重wの固定端モーメントは\(M=\dfrac{w\times L^2}{2}\)で計算し
\(M=\dfrac{w\times l^2}{2}\)
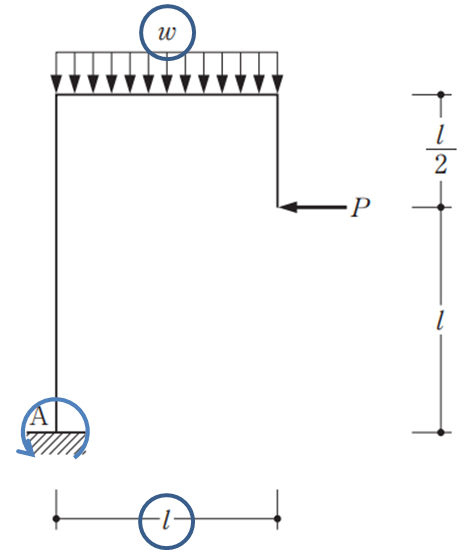
最後に二つの式を等式にすると
\(P\times l=\dfrac{w\times l^2}{2}\)
\(P=\dfrac{w\times l}{2}\)
\(P:wl=2:1\)
したがって固定端モーメントが0になる比率はP:wl=2:1でまとめると答えは③となります。
まとめ
今回は2022年 一級建築士 学科試験Ⅳ構造 No.3の解説をしてきました。
今回の問題のポイントはモーメントの算定のしかたです。比較的簡単な計算方法の問題です。ぜひ必ず解けるのようになって下さい!!
対策
- 荷重数が増える場合
- 台形分布荷重の場合
こちらも自分で問題を作って解いてみるとよいでしょう!!
こちらは過去の類似問題ですので参考にしてください。





コメント