今回は2022年度一級建築士 学科試験Ⅳ構造のNo.5の問題についてまとめていきたいと思います。
今回はトラスの節点法・切断法の問題から出題されています。
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

節点法・切断法ってなんだ?
問題 No.5
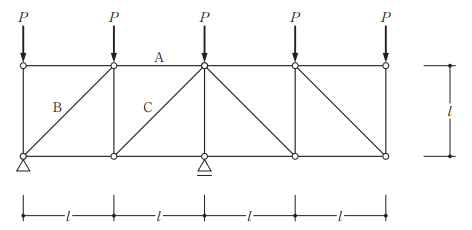
図のような荷重が作用するトラスにおいて、部材A、B及びCに生じる軸方向力をそれぞれNA、NB及びNCとするとき、それらの大小関係として、正しいものは、次のうちどれか。ただし、全ての部材は弾性部材とし、自重は無視する。また、軸方向力は、引張力を「+」、圧縮力を「-」とする。
[選択肢]
- \(N_{A}<N_{B}<N_{C}\)
- \(N_{B}<N_{A}<N_{C}\)
- \(N_{C}<N_{A}<N_{B}\)
- \(N_{C}<N_{B}<N_{A}\)
この問題キーワードは
- 節点法・切断法での解き方
- 力のつり合いの求め方
の2点ですここだけ押さえておけばこの問題を解くことができます。
節点法とは
節点法とはトラス構造物の力学解析に使用される一般的な方法の1つです。節点法で構造物の節点を成分分解して、その節点での力と反力を求めます。
節点法のメリットは力のつり合い式のみから軸力を計算することができるので非常にシンプルな点です。
節点法のデメリットは節点に集まる力の未知数が3コ以上になると解くことが不可能になります。
したがって部材がひとつの節点に集まるモデルの問題があると節点法が使えませんので、そのときは切断法を用いて下さい。
節点法の解き方は
- 支点反力をもとめる
- 反力点や未知数が2つ以下の節点の力のつり合いをもとめる
- 2で解いた節点に隣合う未知数が2つ以下の節点の力のつり合いをもとめる
- 3の繰り返し
節点法の詳しい解説はこちらの記事を参考にしてみて下さい。
切断法とは
切断法とは軸力を求めたい部材を切断し、モーメントのつり合い式から軸力を求めることができる方法を指します。
切断法のメリットは軸力を求めたい部材をすぐに求められる点
切断法のデメリットは切断できる軸力の未知数が4つ以上になると解くことが不可能な点
したがって切断できる箇所は自然と決まるので複雑なトラスには切断法が使えません。
切断法の解き方は
- 支点反力をもとめる
- 部材を仮想的に切断する
- 求めたい軸力を計算できる節点からモーメントのつり合い式を求める
- 求めたい軸力があれば3の繰り返し
切断法の詳しい解説はこちらの記事を参考にしてみて下さい。
またトラス構造物を節点法・切断法で解く上での前提条件は以下のものがあげられます。
トラスは軸力しか負担しません(曲げ・せん断力等は無いものとする)
軸力とは引張力および圧縮力のことです
一般的にトラスの軸力が引張・圧縮どちらなのか判断がつかなくなるので通例的に
・引張力を正(プラス)
・圧縮力を負(マイナス)
として表現します、もちろん逆に考えても支障はありません
つり合い式をたてるときに軸力の向きは

・節点を引くような向きを引張力
・節点を押し込むような向きを圧縮力
と軸力を仮定します。答えが正であれば仮定した軸力の向きで合っており、負であれば仮定した軸力の逆の向きとわかります
解き方
今回は切断法の方が求めたい部材の軸力を瞬時に求めることができるので切断法を用います。
そのうえで問題の解く順序は
- 支点反力をもとめる
- 部材を仮想的に切断する
- 求めたい軸力を計算できる節点からモーメントのつり合い式を求める
- 3の繰り返し
まず最初は支点反力を求めていきます。
左下のピン支点を支点1、中央のローラー支点を支点2とします。その時の支点1まわりの曲げモーメントが0なので
\(M_{1}=Pl+2Pl+3Pl+4Pl-R_{2}*2l=0\)
\(R_{2}=5P\)
鉛直方向の力のつり合いから支点1を出します。
\(R_{1}=0\)
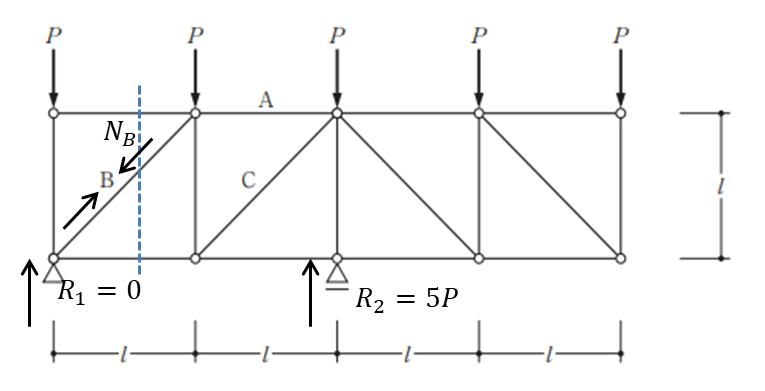
次に部材を切断していきます。部材Bを切り、軸力NBを求めたいと思います。
\(R_{1}=0\)であり、鉛直方向のつり合いと考えると荷重Pに釣合うために節点を引抜く力から引張力NBが働くので以下の等式になります。
\(P=N_{B}/\sqrt{2}\)
\(N_{B}=\sqrt{2}P\)
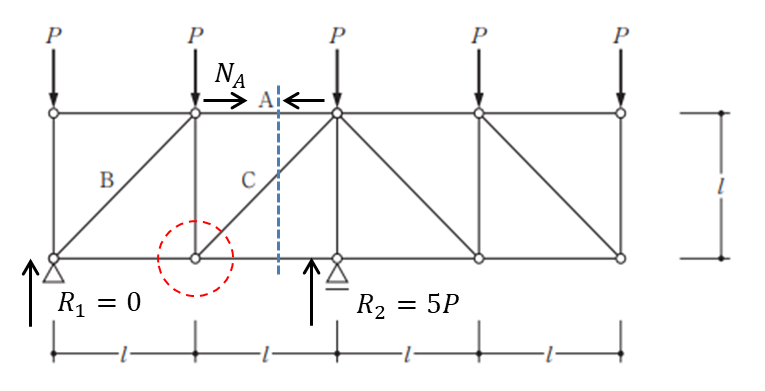
2つ目は部材A・部材Cを切るように切断してみましょう。
赤丸の点でのつり合いと考える部材Cの軸力にかかわらず部材Aの軸力がわかります。切断法を使用した時の力のつり合いは切断されている部材軸力、荷重と反力を用いて等式を立てます。したがって以下のような式となります。(時計回りを正・部材Aの軸力を仮に引張力として計算します。)
\(-Pl+R_{1}l+N_{A}l=0\)
\(N_{A}=P\)
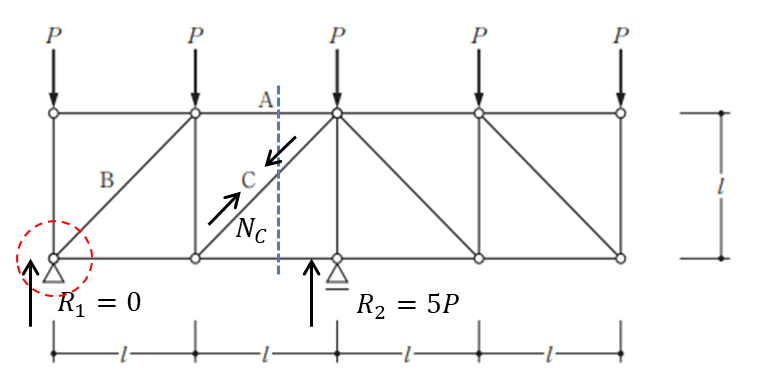
3つ目は部材Cの軸力を調べるために赤丸の点でのつり合いと考えます。切断法を使用した時の力のつり合いは切断されている部材軸力、荷重と反力を用いて等式を立てます。したがって以下のような式となります。(時計回りを正・部材Cの軸力を仮に引張力として計算します。)
\(Pl+N_{A}l-N_{C}\sqrt{2}l/2=0\)
\(N_{C}=\dfrac{4P}{\sqrt{2}}=2\sqrt{2}P\)
答えがプラスなので仮定した引張力であるということもわかりました。
最後にすべてを比較し、
\(N_{A}=P\)、\(N_{B}=\sqrt{2}P\)、\(N_{C}=2\sqrt{2}P\)
\(N_{A}<N_{B}<N_{C}\)
答えは①ということがわかりました。
まとめ
今回は2022年 一級建築士 学科試験Ⅳ構造 No.5の解説をしてきました。
今回の問題のポイントは切断法による計算のしかたです。一見難しそうに見えますが比較的簡単な計算方法の問題です。
節点法・切断法の問題は毎年のように出る頻出問題です。是非解けるようになって下さい!!
傾向と対策
今後の傾向と対策としては
- 荷重数・大きさが増える場合
- トラスがもっと複雑になる場合
こちらも自分で問題を作って解いてみるとよいでしょう!!
以下は過去の類似問題ですのでぜひ参考にしてください。






コメント