今回は2023年度一級建築士 学科試験Ⅳ構造のNo.3の問題についてまとめていきたいと思います
今回は構造力学の崩壊荷重の問題から出題されています
崩壊荷重の問題を初めて見る人も多いとおもいます。この記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

崩壊荷重!!どうやって解くの!?
問題 No.3
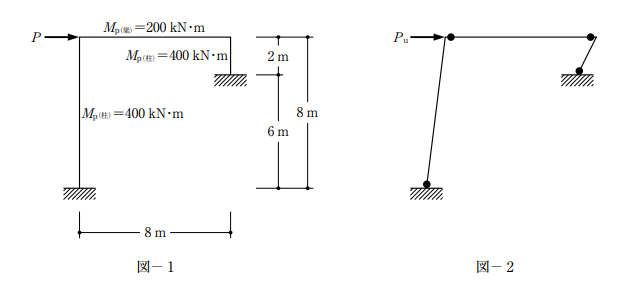
[No.3]
図-1のような水平荷重Pを受けるラーメンにおいて、Pを増大させたとき、そのラーメンは、図-2のような崩壊機構を示した。ラーメンの崩壊荷重Puの値として、正しいものは、次のうちどれか。ただし、柱、梁の全塑性モーメントの値は、それぞれ 400 kN・m、200 kN・mとする。
[選択肢]
- 225kN
- 300kN
- 375kN
- 500kN
この問題キーワードは
- 崩壊荷重の求め方
になります。名前こそ聞き慣れないですが、難しいことはないのでぜひ覚えてください
前提条件

この問題は以下の知識について問われています
- 崩壊荷重
- 仮想仕事の原理
ひとつずつ紐解いていきましょう!!
崩壊荷重とは
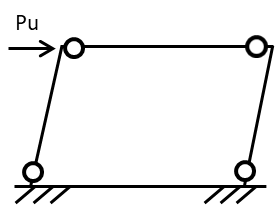
崩壊荷重とは崩壊メカニズム時の荷重を指します。言い換えると建物や構造物は外力(荷重)に対して無限に耐えられることはなく、いつか崩壊します
ある一定の外力(荷重)で梁や柱が降伏していき塑性ヒンジができ、それ以上の耐荷重を増やすことができなくなり『荷重が増えず変形だけが進んでいく状態』や『梁や柱の部材が破壊され一気に崩壊する状態』になる荷重を崩壊荷重といいます
崩壊荷重の記号は[P] や[Pu]で表現されます (Puの”u”はultimateつまり”終局”の意味を表します)
単位は力の[kN]または[N]と表現されます
崩壊荷重の求め方
一級建築士試験の問題でよく出題される崩壊荷重の求め方は仮想仕事の原理に基づきます
仮想仕事の原理とは簡単に言えば外力と内力のつり合った状態を指します
式で表すと
仮想仕事の原理
\(W=Σ(Pu×\delta)=Σ(Mp×\theta)\)
Pu:崩壊荷重
δ:変位あるいは変形
Mp:全塑性モーメント
θ:たわみ角
崩壊荷重の求め方は
- 崩壊荷重時の変形量・たわみ角を仮定する
- 外力(荷重)の仕事量ΣP×δの式をつくる
- 内力(部材耐力)の仕事量ΣM×θの式をつくる
- 仮想仕事の原理の等式(ΣP×δ=ΣM×θ)から導く
詳しい解説についてはこちらの記事を参考にしてみて下さい
解き方
解く順序は
- 崩壊荷重時の変形量・たわみ角を仮定する
- 外力の仕事量の式を作る
- 内力の仕事量の式を作る
- 仮想仕事の原理の等式から導く
ひとつずつ算出していきましょう
1.崩壊荷重時の変形量・たわみ角を仮定する
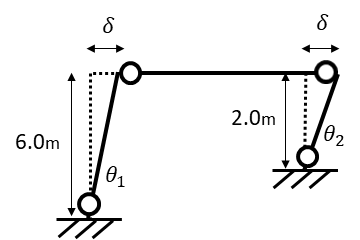
まず崩壊荷重時の層全体の変形量を\(\delta\)と仮定します。
つぎにたわみ角を仮定し、左の柱のたわみ角をθ1,右の柱のたわみ角をθ2とします。柱頭の変位量が同じになるので、
\(\delta=sin\theta_{1}\cdot 8=sin\theta_{2}\cdot 2\) とおきます
ただしたわみ角θが微小であることに限ればsinθ≒θとなるので
\(\delta=\theta_{1}\cdot 8=\theta_{2}\cdot 2\) …(1)
となります。(1)式を解くと
\(\theta_{2}=4\theta_{1}\) となります
2.外力の仕事量の式を作る
つぎに外力の仕事量の式を作ります。外力の仕事量は荷重×変位で表されます。したがって
\(\Sigma W_{o}=Pu\cdot\delta\) …(2)
3.内力の仕事量の式を作る
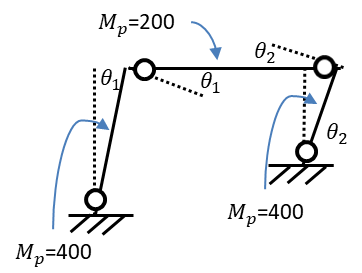
つぎに内力の仕事量の式を作ります。内力とは部材自身の持つエネルギーのようなもので内力の仕事量は全塑性モーメント×部材のたわみ角で表されます
またたわみ角はヒンジのあるところに存在します。柱のたわみ角は簡単に見つかりますが、梁のたわみ角は柱梁が直角に交わるなら接合部を90°に保ち水平からどれくらい角度がついているかを描きます
内力を式で表すと
\(\Sigma W=400\cdot\theta_{1}+200\cdot\theta_{1}+200\cdot\theta_{2}+400\cdot\theta_{2}\)
たわみ角は先ほど \(\theta_{2}=3\theta_{1}\) となったので以下のように変形し
\(=400\cdot\theta_{1}+200\cdot\theta_{1}+200\cdot 4\theta_{1}+400\cdot 4\theta_{1}\)
\(\Sigma W_{i}=3000\cdot\theta_{1}\) …(3)
4.仮想仕事の原理の等式から導く
(1)~(3)式をまとめ、仮想仕事の原理の等式から導くと
\(\delta=8\cdot\theta_{1}\) …(1)
\(\Sigma W_{o}=\Sigma W_{i}\) …(2)
\(Pu\cdot\delta=3000\cdot\theta_{1}\)…(3)
崩壊荷重Puとしてあらわすと
\(Pu=\dfrac{3000\cdot\theta_{1}}{8\theta_{1}}=375\)
答えは『375kN』となり、最終的な答えは③でした
別解
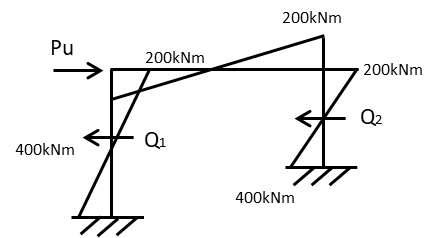
このほかにも柱にかかるせん断力を利用して答えを導く方法もあります
崩壊荷重(水平荷重)=柱のせん断力の合計 を利用して解いていく方法です
まずM図を描きます。M図は引張側にモーメント応力が来るように描き
柱梁接合部は(梁の全塑性モーメント)<(柱の全塑性モーメント)ため梁の全塑性モーメントにして描きます
柱脚は柱の全塑性モーメントです
柱にかかるせん断力はせん断力=柱のモーメント÷柱の長さ で表されるので
左柱のせん断力:\(Q_{1}=(400+200)/8=75\) kN
右柱のせん断力:\(Q_{2}=(400+200)/2=300\) kN
崩壊荷重(水平荷重)=柱のせん断力の合計より
崩壊荷重:\(Pu=Q_{1}+Q_{2}=375\) kN
とより簡単に解くことができます!
まとめ
今回は2023年 一級建築士 学科試験Ⅳ構造 No.3の解説をしてきました
崩壊荷重および仮想仕事の原理については解き方も特殊で忘れてしまう人も多いかと思いますが、たわみ角と変位とヒンジの全塑性モーメントを見つけることができれば簡単に解くことができます
仮想仕事の原理と崩壊荷重については詳しい解説を記事にしていますので、是非崩壊荷重の記事もあわせて是非参考にしてみて下さい!!



コメント