今回は節点法についてわかりやすく解説していきたいと思います。
一級建築士試験におけるトラスの問題は節点法と切断法を用いる頻出問題です。今回はそのひとつの節点法についてまとめたいと思います。ぜひ参考にしてみて下さい。
節点法とは

節点法とは支点における反力を求めた後、支点から出発し順次隣接の節点で力のつり合い式を立てて軸力を求めていく方法を指します
節点法のメリットは力のつり合い式のみから軸力を計算することができるので非常にシンプルな点です。
節点法のデメリットは節点に集まる力の未知数が3コ以上になると解くことが不可能になります。
したがって部材がひとつの節点に集まるモデルの問題があると節点法が使えませんので、そのときは切断法を用いて下さい。
節点法の解き方
節点法の解き方は
- 支点反力をもとめる
- 反力点や未知数が2つ以下の節点の力のつり合いをもとめる
- 2で解いた節点に隣合う未知数が2つ以下の節点の力のつり合いをもとめる
- 3の繰り返し
トラスは軸力しか負担しません(曲げ・せん断力等は無いものとする。) 軸力とは引張力および圧縮力のことです。一般的にトラスの軸力が引張・圧縮どちらなのか判断がつかなくなるので通例的に
・引張力を正(プラス)
・圧縮力を負(マイナス)
として表現します、もちろん逆に考えても支障はありません。つり合い式をたてるときに軸力の向きは

・節点を引くような向きを引張力
・節点を押し込むような向きを圧縮力
と軸力を仮定します。答えが正であれば仮定した軸力の向きで合っており、負であれば仮定した軸力の逆の向きとわかります。
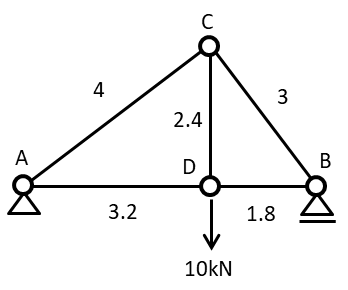
ここで例題を見ながら解いてみましょう。問題例はD点に10kNの荷重が作用しているモデルを想定します
1.支点反力を求める
まずは支点反力を求めます。A点、B点それぞれの反力をRa、Rbとします。
水平方向の力つり合い式ΣH=0はB点ローラー支点とわかればA点の水平反力は0と瞬時に判断しましょう。
鉛直方向の力つり合い式ΣV=0は
\(Ra+Rb=10\) …(1)
A点まわりのモーメントのつり合い式ΣMa=0は
\(10\times3.2-5\times Rb=0\) …(2)
(1)(2)式を計算すると
\(Ra=3.6\)
\(Rb=6.4\)
と求まりました。
2.反力点や未知数が2つ以下の節点の力のつり合いを求める
つぎに反力点や未知数が2つ以下の節点の力のつり合いを求めます。

この場合は反力点Aが求めやすいです A点を拡大してみると、反力Raに対して力のつり合いを考慮すると下向き同じく3.6kNの力が必要となります。
このときの軸力は反力を押さえつける力は圧縮力⊖になります。この際の水平と斜材のなす角θはそれほど必要はなく、別の方法として対比の式を作ります斜辺の力を\(N_{1}\)と置くと、
\(4:2.4=N_{1}:3.6\)
\(2.4N_{1}=14.4\)
\(N_{1}=6\)
斜材の軸力(圧縮⊖)はN1=6kNが求まりました。
水平部材は斜材に対しての水平方向のつり合いなので水平方向の力を\(N_{2}\)と置くと、
\(4:3.2=6:N_{2}\)
\(4N_{2}=19.2\)
\(N_{2}=4.8\)
水平部材は斜材の圧縮につり合いために引張力⊕N2=4.8kN発生しているとわかりました。
3.解いた節点に隣あう未知数が2つ以下の節点の力のつり合いを求める
つぎからは先ほど解いた節点に隣あう未知数が2つ以下の節点の力のつり合いを求めます。
隣あう節点かつ未知数が2つ以下になるのはC点・D点なので解いていきます。

C点は水平方向のつり合いからN3はN2の水平方向の力とつり合うので
N2の水平方向の力をNH2とすると
\(4:3.2=6.0:N_{H2}\)
\(4N_{H2}=19.2\)
\(N_{H2}=4.8\)
\(3:1.8=N_{3}:N_{H2}\)
\(1.8N_{3}=14.4\)
\(N_{3}=8\)
水平力のつり合いを考えるとN3=8kNの圧縮力⊖です
C点の鉛直力のつり合いはN4は両側の斜材の鉛直方向の力とつり合うので
N2の鉛直力をNv2,N3の鉛直力をNv3とすると
\(4:2.4=6:N_{V2}\)
\(4N_{V2}=14.4\)
\(N_{V2}=3.6\)
\(3:2.4=8:N_{V3}\)
\(3N_{V3}=19.2\)
\(N_{V3}=6.4\)
\(N_{4}=N_{V2}+N_{V3}=10\)
(N4は荷重とつり合うので計算しなくとも算出できますが一応計算しました)

D点は十文字なので計算すら不要です圧縮引張の向きだけ気をつけましょう
N2は②で既に解いているので⊕4.8
N5はN2につり合うようにN5=4.8kNの引張力⊕が発生します。
N4は③でも既に解いていますが、鉛直方向に働くのは荷重のみなのでつり合うようにN4=10kNの引張力⊕が発生します。
4.”隣接節点の力のつり合いを求める”の繰り返し
あとはただ隣接節点の力のつり合いを求めていくの繰り返しですのでB点はすでにN3とN5が求まっているので計算の必要がありませんが、節点が続くようであれば繰り返して行っていってください。
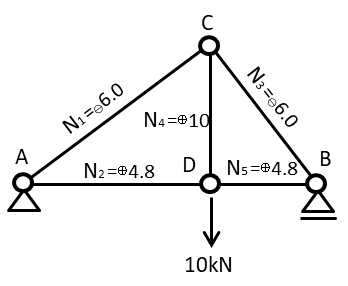
今回はあえて三角比(sin cos etc…)を使わずに解いてみましたもちろん使った方が便利ですし計算も早くなります。
ただ三角比を覚えていない、忘れてしまったときはこの(長さと力の比で解く)方法で試してみて下さい!
具体的な問題
最後に実際にあった一級建築士試験の節点法の問題から解いてみましょう。
節点法の問題

[問題]
モデルA、B、Cに図のような荷重Pをかけたときの水平変位を問われた内容ですがそれぞれの違いは①荷重のかけ方と②下端材の断面積がaまたは2aという違いがあります
この問題のポイントは「節点法の考え方で下端材にかかる軸力を比べること」です。図のような水平変位を起こすときは下端材が伸びに対して抵抗するためです。
したがって下端材にかかる軸力さえわかれば解けます。早速解いてみましょう!
[計算過程]
まずはそれぞれのトラスの支点反力を求めます。
水平反力は左をH1・右をH2とし、鉛直反力は左をV1・右をV2とします。
[トラスA]
\(H_{1}=H_{2}=0\)
\(V_{1}=V_{2}=P/2\)
[トラスB & トラスC]
\(H_{1}=P\)
\(H_{2}=0\)
モーメントのつり合いから
\(2l*V_{2}-P*l=0\)
\(V_{2}=P/2\)
\(V_{1}=-P/2\)

つぎに反力点から軸力を求めてきます。未知数の少ない右の反力R2 から解くと簡単です。
斜材の右の軸力をN1 下端材の軸力をN2とします。
[トラスA]
鉛直のつり合い
\(1:\sqrt{2}=V_{2}:N_{1A}\)
\(N_{1A}=\sqrt{2}*V_{2}=\sqrt{2}P/2\)
水平のつり合い
\(\sqrt{2}:1=\sqrt{2}P/2:N_{2A}\)
\(N_{2A}=P/2\)
[トラスB & トラスC]
\(1:\sqrt{2}=P/2:N_{1B}\)
\(N_{1B}=\sqrt{2}P/2\)
水平のつり合い
\(\sqrt{2}:1=\sqrt{2}P/2:N_{2B}\)
\(N_{2B}=P/2\)
まとめるとすべてのモデルで下端材にかかる軸力がN2=P/2で共通ということがわかりました。
下端材の軸力がわかったところで水平変位を求めるにはヤング係数の知識も必要ですが一般的な考えとして
断面積aと2aどちらか伸びにくいか問われれば自然と2aと答えられるのではないでしょうか!?
詳細に数式で解くなれば、変位はヤング係数のE=σ/εの式から求められ
\(\sigma=P/A\)
\(\varepsilon=δ/L\)
Pは軸力、Aは断面、Lは材長、δは変位量なので
\(δ=\dfrac{N_{2}L}{EA}\)
今回のモデルの断面積はaまたは2aなので断面積の大きい2aの方が変位が小さくなり
答えは『δB<δA=δC』となります。
あわせてこちらもご覧ください。
まとめ
今回は節点法についてまとめてきました。一級建築士試験でも頻出の問題です。節点法は支点反力を求めて、未知数の少ない節点から順に軸力を求めていく方法です
トラスの軸力は向きがつかみにくく、三角比も使わなくてはいけないという認識があると思います。
今回紹介した方法は三角比も使わないかなり噛み砕いた説明したので、この記事を何度も見て勉強してください!!それでは!!




コメント