今回は2021年度一級建築士 学科試験Ⅳ構造のNo.4の問題についてまとめていきたいと思います
今回は構造力学の全塑性モーメント・崩壊荷重から出題されています
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
問題 No.4
[No.4]
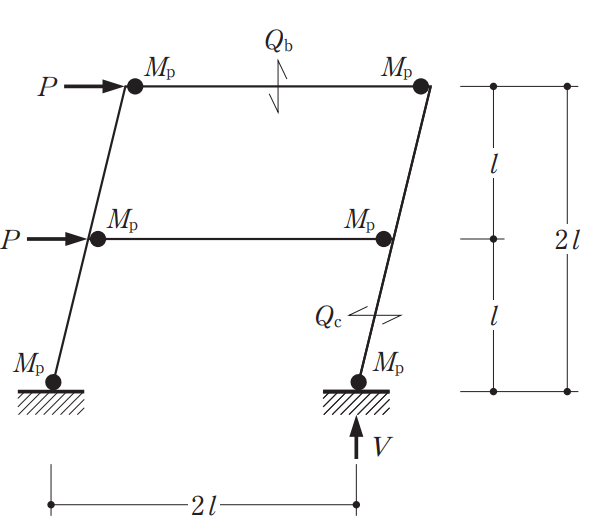
図は、2 層のラーメンに水平荷重P が作用したときの、正しい崩壊メカニズムを示したものである。次の記述のうち、最も不適当なものはどれか。ただし、柱及び梁の全塑性モーメントはMpとする。
[選択肢]
1 図のせん断力QbはMp/lである。
2 図のせん断力Vは2Mp/lである。
3 図のせん断力Pは2Mp/lである。
4 図のせん断力Qcは4Mp/lである。
この問題キーワードは
- 崩壊荷重Pの求め方
- 柱の剛比
だと思います。細かく解説していきます
前提条件
この問題は大きく
・崩壊荷重の求め方
についての知識が問われています。
崩壊荷重
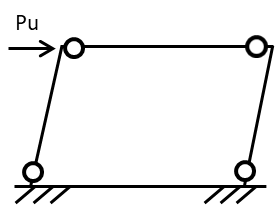
崩壊荷重は崩壊メカニズム時の荷重を指します。シンプルでわかりやすく言えば”崩壊時の荷重”です
崩壊メカニズムの一つに塑性ヒンジが形成された架構の状態があります。一級建築士試験で問われるような崩壊荷重は塑性ヒンジがある架構モデルから仮想仕事の原理から求める問題という認識で大丈夫です。
仮想仕事の原理も混乱しやすいワードではありますが、荷重×変位の外力の仕事量と全塑性モーメント×部材のたわみ角の内力の仕事量がつり合った状態を指します
仕事量は[W]で表し、単位は[kN・mm]や[kN・mm]で曲げモーメントの単位と同じと考えましょう
式で表すと
仮想仕事の原理:\(Σ(Pu×δ)=Σ(Mp×θ)\)
Pu:崩壊荷重
δ:変位量あるいは変形量
Mp:全塑性モーメント
θ:たわみ角
詳しい崩壊荷重の解説はこちらの記事を参考にしてみて下さい
解き方
解く順序は
- 梁のせん断力Qbを求める
- 梁のせん断力から鉛直反力Vを求める
- 仮想仕事の原理から崩壊荷重Pを求める
- 崩壊荷重Pから柱のせん断力Qcを求めます
ひとつずつ解いていきましょう
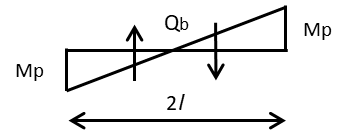
まず初めに梁のせん断力Qbを求めていきましょう。ここは崩壊荷重と関係なく解くことができます。梁のせん断力は端部のモーメントの合計÷梁の長さで求められます。モーメント=せん断力×梁の長さで求められるので結局は同じことです
\(Q_{b}=\dfrac{Mp+Mp}{2l}=\dfrac{Mp}{l}\) …(1)
このように梁のせん断力Qbを求めることができました
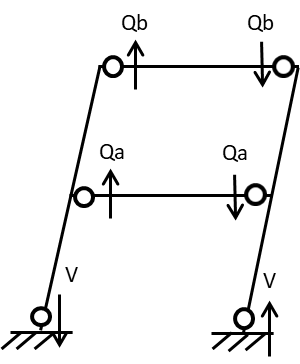
つぎに梁のせん断力から鉛直反力Vを求めていきましょう。力のつり合いより鉛直方向にかかる荷重がないため、右下の鉛直反力=2層の梁の右端のせん断力+1層の梁の右端のせん断力 で求められます。(注:ただし鉛直荷重が作用するとこの等式は成り立ちません)
2層の梁のせん断力Qbが先ほど求まったので、同じく1層の梁のせん断力Qaとおいて先ほどと同じ要領で解いていきます
\(Q_{a}=\dfrac{Mp+Mp}{2l}=\dfrac{Mp}{l}\) …(2)
梁のせん断力がそろったところで鉛直反力と梁のせん断力がつり合うので、(1)(2)式より
\(V=Q_{a}+Q_{b}=\dfrac{Mp}{l}+\dfrac{Mp}{l}=2\dfrac{Mp}{l}\)
このように右側の鉛直反力Vを求めることができました
つぎに仮想仕事の原理から崩壊荷重Pを求めます。
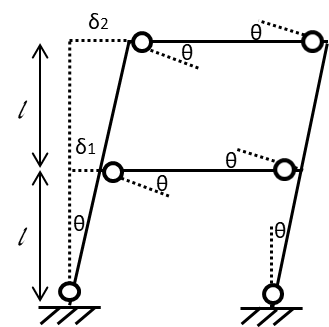
まずは変位量とたわみ角を仮定します。たわみ角がなぜすべて同じなるかと言えば変位量が一直線上に増えているためヒンジ部の接合部は同じたわみ角になります。
たわみ角の図を描くときは90°を保つように絵を描くと直感的にわかります。
仮定できたらたわみ角とたわみ量の関係を部材の長さを使って表します。
1層のたわみをδ1
2層のたわみをδ2
とすれば、たわみ角と部材の長さを使うと
1層のたわみ角:\(δ_{1}=θ・lδ_{1}=θ・l\) …(a)
2層のたわみ角:\(δ_{2}=θ・2lδ_{2}=θ・2l\) …(b)
と表現できます。ここでやっと仮想仕事の原理を使います。
外力のなす仕事量は
\(ΣW=P⋅δ_{1}+P⋅δ_{2}ΣW=P⋅δ_{1}+P⋅δ_{2}\) …(c)
内力のなす仕事量は
\(ΣW=(Mpθ+Mpθ+Mpθ)×2=6Mpθ\) …(d)
(a)~(d)の式をまとめると
\(P⋅δ_{1}+P⋅δ_{2}=6Mpθ\)
\(P⋅θl+P⋅θ・2l=6Mpθ\)
\(P=\dfrac{2Mp}{l}\)
このように崩壊荷重Pを求めることができました
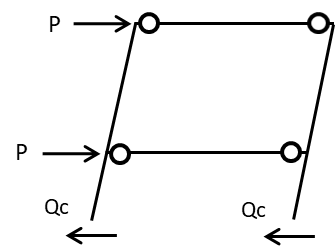
最後に崩壊荷重Pが求まったことで柱のせん断力を求めます。これは共通してかなり重要で当たり前のことですが、
地震力や風圧力のようなは水平力は柱にせん断力はとして伝達され下階そして地面に流れていくことです。
つまりは1階の柱のせん断力の合計は上階から伝わるすべてのせん断力(水平力)とつり合います。これは真理なのでいかなる場合でも成り立ちます。
したがって崩壊荷重(水平荷重)=1階の柱のせん断力の合計より、1層の柱の長さおよび全塑性モーメントのが同じであるので柱の剛性等しくなるので右左の柱せん断力は等しくなり
\(2P=Qc+Qc=2Qc\)
\(P=\dfrac{2Mp}{l}\)
\(Qc=\dfrac{2Mp}{l}\)
このように柱せん断力Qcを求めることができました
したがって最終的な答えは④でした
まとめ
今回は2021年 一級建築士 学科試験Ⅳ構造 No.4の解説をしてきました
この問題は崩壊荷重で受験生が嫌う問題のひとつです。しかしひとつずつ紐解いていくと全然難しくないので、この記事を何度も読み返し、是非とも間違えずに答えてもらいたい問題です




コメント