今回は2022年度一級建築士 学科試験Ⅳ構造のNo.6の問題についてまとめていきたいと思います。
今回はせん断力図の問題から出題されています。
なかなかせん断力を描く機会がない人も多いとおもいますので、この記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

せん断力図ってなんだ?
問題 No.6
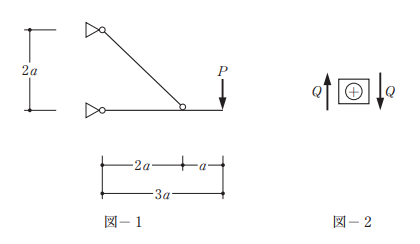
図-1 のような構造物に鉛直荷重P が作用したときのせん断力図として、正しいものは、次のうちどれか。ただし、全ての部材は弾性部材とし、自重は無視する。また、せん断力の符号は図-2 に示した向きを「+」とする。
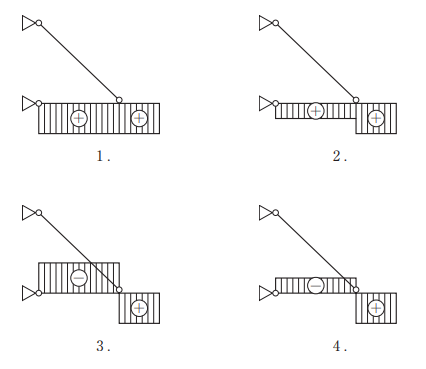
[選択肢]
この問題キーワードは
- 力のつり合いの求め方
- 力の成分分解について
の2点ですここだけ押さえておけば簡単にこの問題を解くことができます。
力のつり合いとは
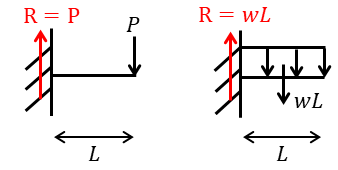
力のつり合いとはある荷重Pを加えたときその反力として荷重と同じ反力Pが必ず発生します。等分布荷重wであれば荷重長(梁長)Lをかけた反力wLが生じます。
力のつり合い式は基本的には2軸(水平方向と鉛直方向)があります。
せん断力は部材の直行方向(図でいえば上下方向)軸力は部材と平行方向(図でいえば左右方向)に分解します。
力の成分分解とは

力の成分分解とは斜めの力を水平方向・鉛直方向の力に分解することです。
基本的には直角2等辺三角形の1:1:√2 と 直角三角形の1:√3:2 を覚えておけば十分です。
解き方
今回の問題を解く順序は
- 支点反力をもとめる
- 端部からせん断力を計算していく
まずは支点反力を求めていきます。算出しやすい水平方向から行います。
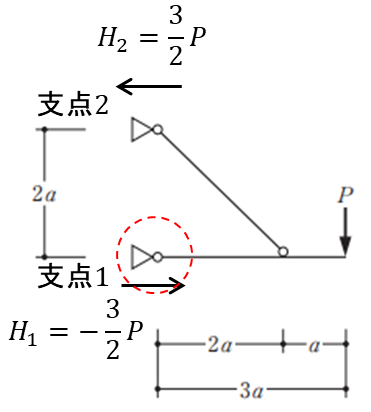
左下のピン支点を支点1、左上のローラー支点を支点2とします。
支点1まわりの曲げモーメントを算出します。ピン支点はモーメントが0になるので(時計回りを正・反時計周りを負)
\(M_{1}=3Pa-H_{2}*2a=0\)
\(H_{2}=\dfrac{3}{2}P\)
水平方向の力のつり合いから
\(H_{1}=-\dfrac{3}{2}P\)
次に鉛直方向の反力を計算していきます。斜材を切り、軸力Nを求めたいと思います。
水平方向にH2の反力があるので、斜材の軸力はH2×√2になります。
\(N=H_{2}\sqrt{2}=\dfrac{3\sqrt{2}}{2}P\)
同じく鉛直方向の反力を斜材の軸力から求めると
\(V_{2}=\dfrac{3}{2}P\)
鉛直方向の反力のつり合いと考えるとV2とつり合うように
\(V_{1}=\dfrac{3}{2}P-P=\dfrac{1}{2}P\)
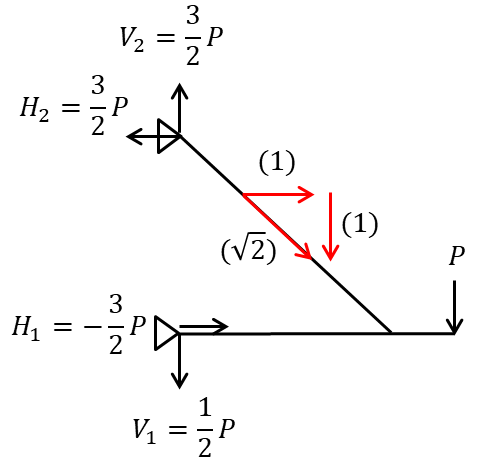
ここまで解くことができれば必要な情報のみで整理をします。せん断力は部材の軸直交方向の力のみを表示させます。
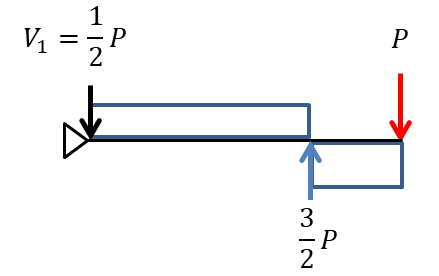
答えは④ということがわかりました。
まとめ
今回は2022年 一級建築士 学科試験Ⅳ構造 No.6の解説をしてきました。
今回の問題のポイントは力のつり合いによる反力の計算のしかたです。一見難しそうに見えますが比較的簡単な計算方法の問題です。
力のつり合いの問題は毎年のように出る頻出問題です。是非解けるようになって下さい!!
傾向と対策
今後の傾向と対策としては
- 荷重数・大きさが増える場合
- 荷重を等分布になる場合
- 切断法を使う場合
こちらも自分で問題を作って解いてみるとよいでしょう!!
以下は過去の類似問題ですのでぜひ参考にしてください。





コメント