今回は2022年度一級建築士 学科試験Ⅳ構造のNo.7の問題についてまとめていきたいと思います。
今回は水平剛性の問題から出題されています。
水平剛性はなかなか理解できない人も多いとおもいますので、この記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

水平剛性ってなんだ?
問題 No.7
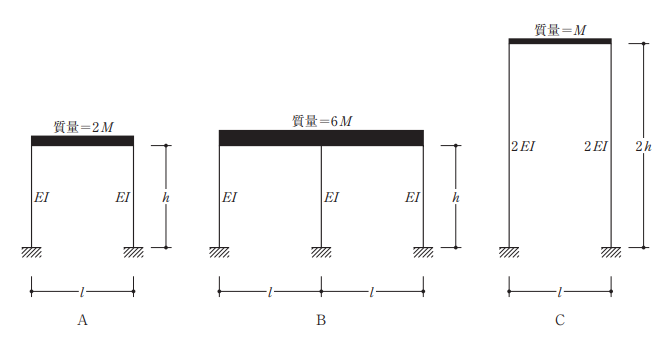
図のようなラーメン架構A、B及びCの水平方向の固有周期をそれぞれTA、TB及びTCとしたとき、それらの大小関係として、正しいものは、次のうちどれか。ただし、柱の曲げ剛性は図中に示すEI あるいは 2EI とし、梁は剛体とする。また、柱の質量は考慮しないものとする。
[選択肢]
- \(T_{A}<T_{B}=T_{C}\)
- \(T_{B}<T_{A}<T_{C}\)
- \(T_{B}=T_{C}<T_{A}\)
- \(T_{C}<T_{A}<T_{B}\)
この問題キーワードは
- 水平剛性の求め方
- 固有周期の求め方
の2点ですここだけ押さえておけば簡単にこの問題を解くことができます。
水平剛性とは
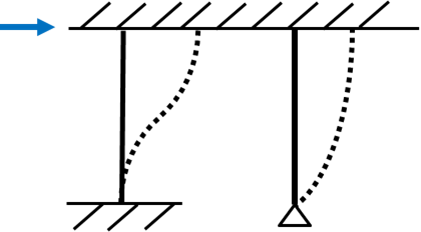
水平剛性(英:horizontal stiffness)とは梁や床をなしている層に対してある一定の力が水平方向(横)からかけられると、層は力と同じ向きに水平移動します。
水平の移動量に対して柱や壁は抵抗しようと逆向きにバネのような抵抗力がはたらきます。このときの水平方向の抵抗力を水平剛性あるいは柱や壁(鉛直部材)による水平方向の硬さとも言えます。建物や建築で言う水平剛性は耐震性とも言えます。
水平剛性は高層ビルなど縦に長い建物を例えるとイメージしやすいです。地震のような水平力を受け横に揺れたとき、水平剛性が大きいがっちりとした建物であれば揺れは小さく、水平剛性が小さいやわらかい建物であれば揺れは大きくなります。
一般的にの記号は[k]や[K]で表されることが多く、単位は[N/mm]や[kN/m]で表されることが多いです。
水平剛性の特徴
水平剛性の特徴は単に水平剛性が大きければいいということでなく、剛性が大きくなるぶん、力を集中的に受けやすくなるので柱や壁にヒビや亀裂が多り損傷が多くなります。
逆に水平剛性が小さいと部材がしなりやすく部材が損傷しにくくなる一方で、揺れは大きくなるので家具や中にいる人は横に大きく揺れるので被害が大きくなります。
水平剛性の公式
水平剛性の公式はフックの法則から求めることができます。
水平剛性 \(k=\dfrac{Q}{\delta}\)
Q:水平力(層せん断力)
δ:水平変位
フックの法則(力=バネ×変位)は
\(Q=k\cdot\delta\)
式変形することで上記の式を導くことができます。
このときの水平変位δを片持梁-集中荷重のたわみの変位量δ=QL3/3EIに置き換えることでQとδを使わずに表現することでき、一級建築士試験では以下の式が多用されます。
ピン支点-水平剛性 \(k=\dfrac{3EI}{L^3}\)
固定支点-水平剛性 \(k=\dfrac{12EI}{L^3}\)
E:ヤング係数
I:断面二次モーメント
L:部材長
水平剛性の詳しい解説はこちらの記事を参考にしてみて下さい。
固有周期とは
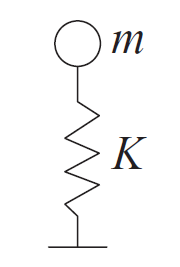
固有周期(英:natural period)とは建物などの物体の揺れが1往復するのにかかる時間を指します。
固有周期は質量や水平剛性、高さなどの要因によって決まります。
固有周期の記号は[T]つまり時間で表され、単位は[s]や[sec]の一秒単位で表します。
式で表すと
固有周期 \(T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{K}}\)
K:ばね剛性
m:質量
ω:固有円振動数、角速度
固有周期の詳しい解説はこちらの記事を参考にしてみて下さい。
解き方
今回の問題を解く順序は
- 柱の水平剛性を求める
- 架構ごとの固有周期を求める
まずは水平剛性を求めていきます。水平剛性の記号を左から順にKA、KB、KCとします。

\(K_{A}=\dfrac{12EI}{h^3}\times 2=\dfrac{24EI}{h^3}\)
\(K_{B}=\dfrac{12EI}{h^3}\times 3=\dfrac{36EI}{h^3}\)
\(K_{C}=\dfrac{12\times 2EI}{(2h)^3}\times 2=\dfrac{6EI}{h^3}\)
水平剛性がわかったことでつぎに固有周期を求めます。
\(T_{A}=2\pi\sqrt{\dfrac{2M}{K_{1}}}=2\pi\sqrt{\dfrac{2M}{\frac{24EI}{h^3}}}\)
\(T_{B}=2\pi\sqrt{\dfrac{6M}{K_{2}}}=2\pi\sqrt{\dfrac{6M}{\frac{36EI}{h^3}}}\)
\(T_{C}=2\pi\sqrt{\dfrac{M}{K_{3}}}=2\pi\sqrt{\dfrac{M}{\frac{6EI}{h^3}}}\)
\(T_{A}=2\pi\sqrt{\dfrac{Mh^3}{12EI}}\)
\(T_{B}=2\pi\sqrt{\dfrac{Mh^3}{6EI}}\)
\(T_{C}=2\pi\sqrt{\dfrac{Mh^3}{6EI}}\)
ここまで解くことができればあとは整理をします。
\(T_{A}<T_{B}=T_{C}\)
答えは①ということがわかりました。
まとめ
今回は2022年 一級建築士 学科試験Ⅳ構造 No.7の解説をしてきました。
今回の問題のポイントは水平剛性の計算のしかたです。一見難しそうに見えますが比較的簡単な計算方法の問題です。
水平剛性問題は隔年ごとに見かけるレベルの頻出問題です。是非解けるようになって下さい!!
傾向と対策
今後の傾向と対策としては
- 柱の本数が増える場合
- 支点の条件がピン・剛ともに共存する場合
こちらも自分で問題を作って解いてみるとよいでしょう!!
以下は過去の類似問題ですのでぜひ参考にしてください。






コメント