今回は2023年度一級建築士 学科試験Ⅳ構造のNo.2の問題についてまとめていきたいと思います。
今回は材料力学の変位量の問題から出題されています。
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

変位の計算方法ってどうやるんだっけ!?
問題 No.2
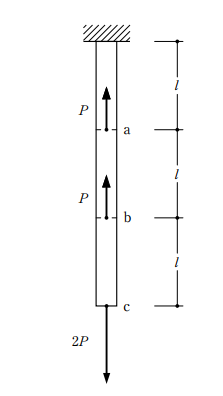
図のような断面積が一定で長さが 3lの部材において、a、b及びcの位置における断面の図心にそれぞれ軸方向力P、P及び 2Pが矢印の向きに作用するとき、「a-b間の軸力」と「cの軸方向変位」との組合せとして、正しいものは、次のうちどれか。ただし、部材は全長にわたって等質等断面の弾性部材とし、自重は無視する。また、部材の断面積をA、ヤング係数をEとする。
[選択肢] a-b間の軸力・cの軸方向変位
- \(P\) ・ \(\dfrac{2l}{AE}P\)
- \(P\) ・\(\dfrac{3l}{AE}P\)
- \(2P\) ・\(\dfrac{2l}{AE}P\)
- \(2P\) ・\(\dfrac{3l}{AE}P\)
この問題キーワードは
- 軸力の算出法
- 変位の算出法
前提条件

この問題はまず軸力の算出と変位の算出について理解する必要があります。
軸力とは
軸力とは部材の軸方向にかかる力を指します。軸力には引張と圧縮の方向性があります。
記号は[N]で表すことが多く、圧縮はマイナス 引張はプラスで表記します。
単位はおもに[kN]や[N]で表すことが多いです。
変位の求め方
変位を式で表すと
\(\Delta l=\dfrac{PL}{AE}\)
Δl:変位量
P:軸力
A:断面積
L:材長
E:ヤング係数
今回の問題で難しいのは材長Lの取り方かと思います、以下で解説します。
解き方
今回の問題の解く順序は
- 反力・部材の節点間にかかる軸力の算定
- N図の作図
- 変位量の算定
ひとつずつ算出していきましょう。
まず反力を算定しましょう、引張を+、圧縮を-とします。
支点の反力は
\(\Sigma=2P-P-P=0\)
支点からa点までの部材の軸力は
0kN
a点からb点までの部材の軸力は
\(N_{ab}=2P-P=P\)
b点からc点までの部材の軸力は
\(N_{bc}=2P\)
次に上記の軸力からN図を描くと
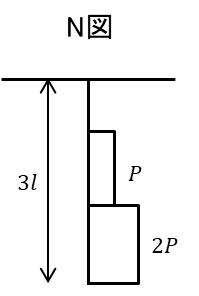
最後に変位を求めます。今回の変位算出で重要なのはcの初期位置からの動いた変位の合計です。
軸力のある箇所に変位のありますが、
そこだけに注目するだけになく部材全体で判断する必要があります。
したがって変位は
a点からb点の変位は
\(N_{ab}=P\)
\(\Delta l_{ab}=\dfrac{Pl}{AE}\)
b点からc点の変位は
\(N_{bc}=2P\)
\(\Delta l_{bc}=\dfrac{2Pl}{AE}\)
これらを合計すると
\(\Delta l_{ab}+\Delta l_{bc}=\dfrac{3Pl}{AE}\)
上記をまとめると答えは②となります。
まとめ
今回は2023年 一級建築士 学科試験Ⅳ構造 No.2の解説をしてきました。
今回の問題は久しぶり出題された変位を求める問題です。
変位を求める際は全部材の軸力から変位量の合計を求めることに気を付けましょう!




コメント