今回は2021年度一級建築士 学科試験Ⅳ構造のNo.1の問題についてまとめていきたいと思います
今回は材料力学の応力の問題から出題されています
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
問題 No.1
[No.1]
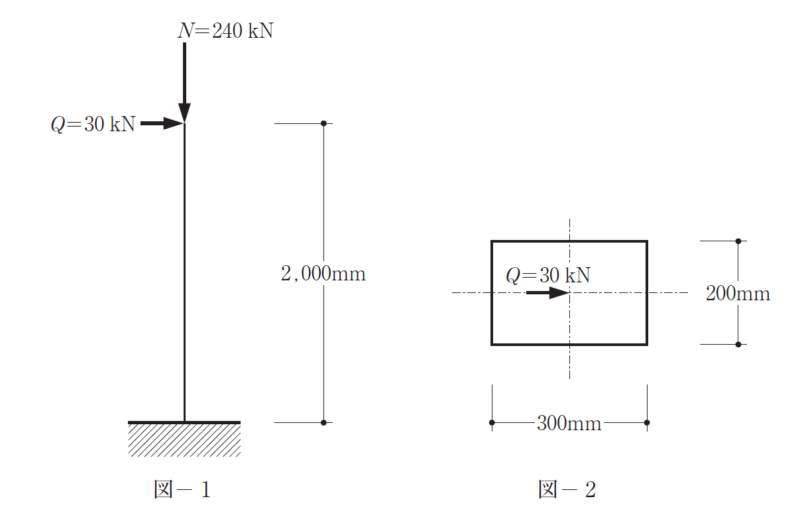
図-1 のように、脚部で固定された柱の頂部に、鉛直荷重N及び水平荷重Qが作用している。柱の断面形状は図- 2 に示すような長方形断面であり、N及びQは断面の図心に作用しているものとする。柱脚部断面における引張縁応力度、圧縮縁応力度及び最大せん断応力度の組合せとして、正しいものは、次のうちどれか。ただし、柱は全長にわたって等質等断面の弾性部材とし、自重は無視する。また、引張応力度を「+」、圧縮応力度を「-」とする。
この問題キーワードは
- 引張・圧縮縁応力度
- 最大せん断力応力度と平均せん断応力度の違い
前提条件
この問題はまず長方形の部材に対して圧縮力(軸力)とせん断力(水平力)さらにはせん断力による曲げモーメントが存在することから始まります
まずは応力度の種類3つ覚えておく必要があります
軸応力度
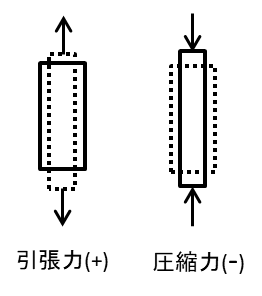
軸応力度とはまたの名を引張応力度・圧縮応力度のことを指し、部材の軸方向の応力度を指します
軸の向きには圧縮方向・引張方向があるのでそれぞれ±で表現します
記号は[σc]または[σt]で表し、cは圧縮の”compression”、tは引張の”tension”です。単位は[N/mm2]です
式は
軸応力度:\(σ=\dfrac{P}{A}\)
P:軸方向力
A:断面積
せん断応力度

せん断応力度とは部材の軸直行方向の応力度を指します
せん断応力度の重要なところは断面内で応力度分布が一様ではないことです
詳しくはこちらをご覧ください
記号は[τ]で表し、単位は[N/mm2]です
式は
最大せん断応力度:\(τ=\kappa\dfrac{Q}{A}\)
平均せん断応力度:\(τ=\dfrac{Q}{A}\)
Q:軸直行力(水平力)
A:断面積
κ:最大応力度/平均応力度
曲げ応力度
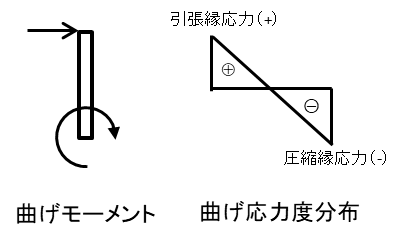
曲げ応力度とは曲げモーメントによる断面内の応力度を指します
曲げ応力度の重要なところは断面内で応力度が一様ではなく、中立軸を境に圧縮応力と引張応力が切り替わります
曲げ応力度は断面端部が最も応力度が大きくなるため圧縮応力縁応力度・引張縁応力度と表現されることが多いです
記号は[σb]で表し、bは曲げの”bending”です。単位は[N/mm2]です
式は
曲げ応力度:\(σ_{b}=\dfrac{M}{Z}\)
M:曲げモーメント
Z:断面係数
解き方
解く順序は
- 軸応力度の算出
- せん断応力度の算出
- 曲げ応力度の算出(および断面係数の算出)
- 軸応力度と曲げ応力度の合成
ひとつずつ算出していきましょう
軸応力度σの算出には軸力と断面積が必要です。必要となる柱脚での軸力はN=240kN(圧縮)と断面積A=200・300=6.0×104 mm2なので
\(σ_{c}=\dfrac{N}{A}\)
\(σ_{c}=\dfrac{240*10^3}{6.0*10^4}=4.0N/mm^2\)
したがって断面内には4.0N/mm2 の圧縮力が一様に働いています
つぎにせん断応力度τはQ=30kN(水平力)と断面積A=200・300=6.0×104 mmによるので
今回必要となるのは最大せん断力応力度なのでκが必要です
長方形断面のκ=3/2なので
\(τ=\kappa\dfrac{Q}{A}\)
\(τ=\dfrac{3}{2}\times\dfrac{30*10^3}{6.0*10^4}=0.75N/mm^2\)
最大せん断力応力度のκの詳しい解説はこちらの記事を参考してください
つぎに曲げ応力度σbはまず曲げモーメントを算出します
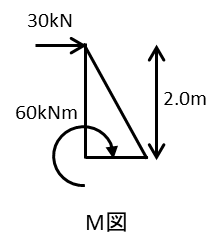
Q=30kN(水平力)と荷重点から柱脚までの距離2000mmなので
\(M=30\times 2.0=60kNm\)
つぎに断面係数Zが必要です
\(Z=\dfrac{200*300^2}{6}\)
\(Z=3.0*10^6mm^3\)
したがって曲げ応力度(引張縁応力度および圧縮力縁応力度)は
\(σ_{b}=\dfrac{60*10^6}{3.0*10^6}=-20N/mm^2\)
曲げ応力度を算出する際は単位を[N/mm2]に揃えて下さい(単位変換も非常に重要)
最後に軸応力度と曲げ応力度を合成します圧縮応力度を『-』引張応力度を『+』とするので
圧縮縁応力度
\(-σ_{b}-σ_{c}=-20-4=-24N/mm^2\)
引張縁応力度
\(σ_{b}-σ_{c}=20-4=16N/mm^2\)
上記をまとめると『引張縁応力:16N/mm2 圧縮縁応力:-24N/mm2 最大せん断力応力度:0.75N/mm2』となります
まとめ
今回は2021年 一級建築士 学科試験Ⅳ構造 No.1の解説をしてきました
今回の問題での引っかけポイントは最大せん断力応力度と平均せん断応力度です。せん断応力度の分布が一様ではないことを予め知っておかなければ解くことができない問題でした
多くの人が平均せん断応力度で答えてしまったのではないでしょうか!?
是非せん断応力度についての記事もあわせて参考にしてみて下さい
・断面が長方形ではなく円形になった場合
・平均せん断応力度を求めることになった場合
・荷重が1か所でなく複数か所になった場合
・柱頭に曲げモーメントMがある場合
こちらも自分で問題を作って解いてみるとよいでしょう!!




コメント