今回は2021年度一級建築士 学科試験Ⅳ構造のNo.5の問題についてまとめていきたいと思います
今回は構造力学のトラス構造・ヤング係数から出題されています
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!
問題 No.5
[No.5]
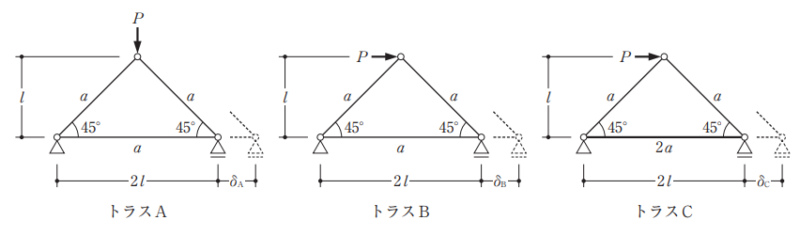
図のような集中荷重P を受けるトラスA、トラスB及びトラスCにおいて、それぞれのローラー支持点の水平変位δA、δB及びδCの大小関係として、正しいものは、次のうちどれか。ただし、各部材は同一材質の弾性部材とし、斜材の断面積はいずれもa、水平材の断面積はトラスA及びトラスBがa、トラスCが 2aとする。
[選択肢]
1 δA = δC < δB
2 δA < δC < δB
3 δC < δA = δB
4 δC < δA < δB
前提条件
この問題キーワードは
- 節点法・切断線
- ヤング係数と軸力の関係式
だと思います。細かく解説していきます
節点法・切断線とは
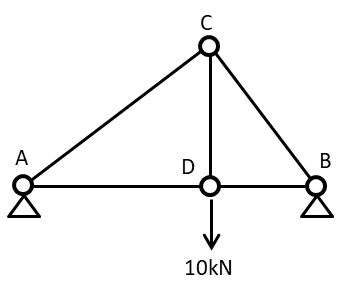
節点法とは支点における反力を求めた後、支点から出発し順次隣接の節点で力のつり合い式を立てて軸力を求めていく方法を指します
節点法のメリットは、力のつり合い・モーメントのつり合い式から軸力を計算することができるので非常にシンプルな点です。
切断線とは軸力を求めたい部材を切断しモーメントのつり合い式から軸力を求めることができる方法を指します
切断法のメリットは、軸力を求めたい部材をすぐに求められる点です
[節点法]
① 支点反力をもとめる
② 反力点や未知数が2つ以下の節点の力のつり合いをもとめる
③ 2で解いた節点に隣合う未知数が2つ以下の節点の力のつり合いをもとめる
④ 3の繰り返し
[切断法]
① 支点反力をもとめる
② 部材を仮想的に切断する
③ 求めたい軸力を計算できる節点からモーメントのつり合い式をたてて軸力を求める
節点法・切断法の使い分けは、節点数が少なく求めたい軸力の数が多い時には節点法。節点数が多く求めたい軸力の数が少ない時には切断法を用いるといいです。
今回の問題では節点数も少なく節点法で十分かと思います。もちろん切断法でも解くことができます。詳しくは以下の記事を参考にしてください!!
ヤング係数とは
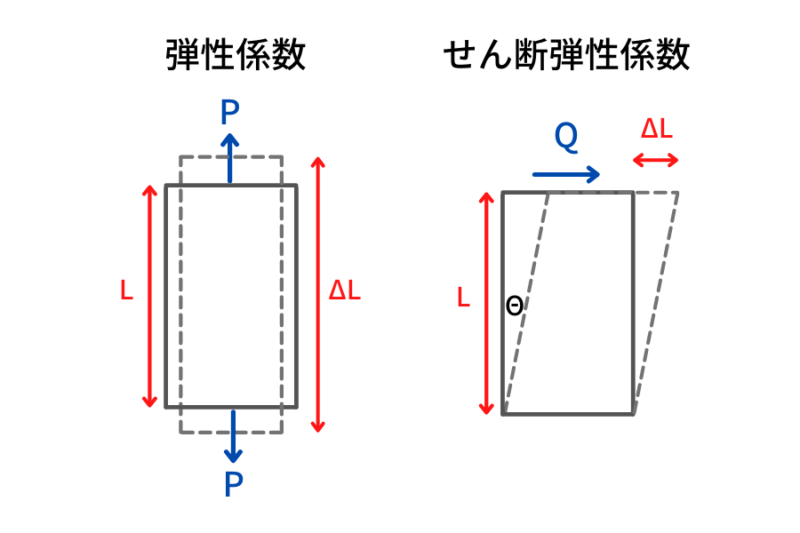
ヤング係数(英:young modulus)は材料による硬さ、剛性を表すパラメータです。
ヤング係数が大きいほど材料が固く、曲がりにくくヤング係数が小さくなるほど柔らかく曲がりやすいです。弾性係数、弾性率、ヤング率、縦弾性係数などいろいろな呼び方がありますが意味は同じです!!
記号は[E]で表します。単位は[N/mm2]で表示することが多いです。
ヤング係数の求め方は
\(E=\dfrac{\sigma}{\varepsilon}\)
σ:応力度(N/mm2)
ε:ひずみ(無次元) =ΔL/L
応力度σは垂直応力度・せん断応力度・曲げ応力度があります。応力度の式は
[垂直応力度] \(\sigma=\dfrac{P}{A}\)
[平均せん断応力度] \(\tau=\dfrac{Q}{A}\)
[曲げ応力度] \(\sigma_{b}=\dfrac{M}{Z}\)
τ:せん断応力度(N/mm2)
P:軸力(N)
Q:せん断力(N)
M:曲げモーメント(N・mm2)
A:断面積(mm2)
Z:断面係数(mm3)
解き方
解く順序は
- 支点反力を求める
- 節点法により軸力を求める
- 軸力から変位(ひずみ)を求める
ひとつずつ解いていきましょう
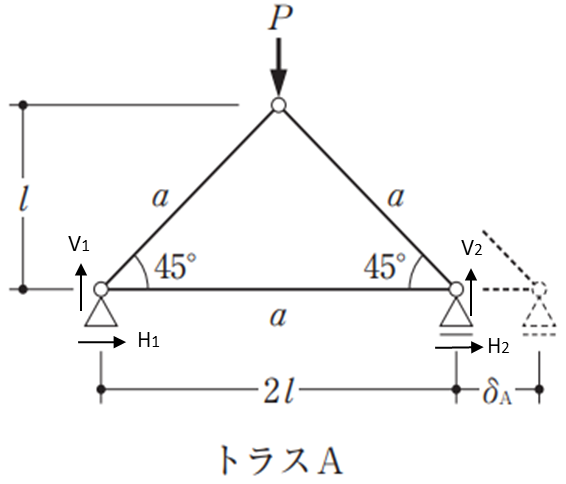
まず初めにを支点反力を求めていきましょう。水平反力は左をH1・右をH2とし、鉛直反力は左をV1・右をV2とします。
[トラスA]
\(H_{1}=H_{2}=0\)
\(V_{1}=V_{2}=P/2\)
[トラスB & トラスC]
\(H_{1}=P\)
\(H_{2}=0\)
左側の支点周りのモーメントのつり合いから
\(2l・V_{2}−P・l=0\)
\(V_{2}=P/2\)
\(V_{1}=−P/2\)

つぎに反力点から軸力を求めてきます。未知数の少ない右の反力V2 から解くと簡単です。右側斜材の軸力をN1 下側部材の軸力をN2とします。
[トラスA]
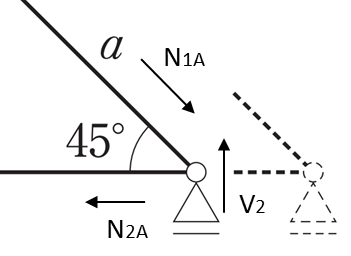
鉛直のつり合い:
\(1:\sqrt{2}=V_{2}:N_{1A}\)
\(N_{1A}=\sqrt{2}\cdot V_{2}=\dfrac{\sqrt{2}}{2}P\)
水平のつり合い:
\(\sqrt{2}:1=\dfrac{\sqrt{2}}{2}P:N_{2A}\)
\(N_{2A}=P/2\)
[トラスB & トラスC]
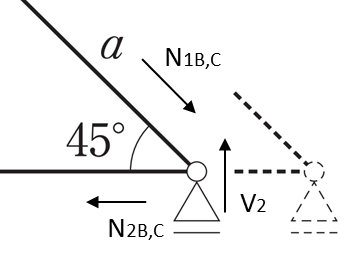
鉛直のつり合い:
\(1:\sqrt{2}=P/2:N_{1B,C}\)
\(N_{1B,C}=\dfrac{\sqrt{2}}{2}P\)
水平のつり合い:
\(\sqrt{2}:1=\dfrac{\sqrt{2}}{2}P:N_{2B,C}\)
\(N_{2B,C}=P/2\)
まとめるとすべてのモデルで下側部材にかかる軸力がN2=P/2で共通ということがわかりました。
最後に軸力から変位(ひずみ)を求めていきます。
下端材の軸力がわかったところで水平変位を求めるには変位と軸力の関係にヤング係数が関係がわかるかどうかです。トラス構造は部材に軸力のみが作用するのでヤング係数に使う応力度は垂直応力度を用います。ヤング係数と応力度の式は
\(E=\dfrac{\sigma}{\varepsilon}\)
\(\sigma=P/A\)
なので式を変換していくと
\(E=\dfrac{PL}{A\cdot\Delta L}\)
P⇒N2 、ΔL⇒δ、L⇒2l、A⇒aまたは2aに変換し、δA・δB・δC を比較します
\(\delta_{A}=\dfrac{P\cdot l}{aE}\)
\(\delta_{B}=\dfrac{P\cdot l}{aE}\)
\(\delta_{C}=\dfrac{P\cdot l}{2aE}\)
したがってδC < δA = δB
ヤング係数の知識も重要ですが一般的な考えとして、面積aと2aを比較してどちらの部材が伸びにくいか問われれば自然と2aと答えられるのではないでしょうか!?
したがって最終的な答えは③でした
まとめ
今回は2021年 一級建築士 学科試験Ⅳ構造 No.5の解説をしてきました
この問題は節点法・切断法で受験生が嫌う問題のひとつです。また変位と軸力の関係からヤング係数の式を導き出せた受験生も少ないのではないでしょうか、もし仮にヤング係数を思い出せずとも一般的な教養でも解けるので、迷ったら自分の直感を信じましょう。
論理的に解きたいのであればぜひこの記事を何度も読み返し答えてもらいたい問題です
・斜材の断面積が異なる場合
・トラスが複雑になる場合(切断法をつかう)




コメント