今回は2022年度一級建築士 学科試験Ⅳ構造のNo.2の問題についてまとめていきたいと思います。
今回は材料力学のたわみの問題から出題されています。
聞き慣れないワードもあるかとおもいますのでこの記事では初学者でも理解できるようにわかりやすく説明していきたいと思います!

たわみ量の計算方法ってどうやるんだっけ!?
問題 No.2
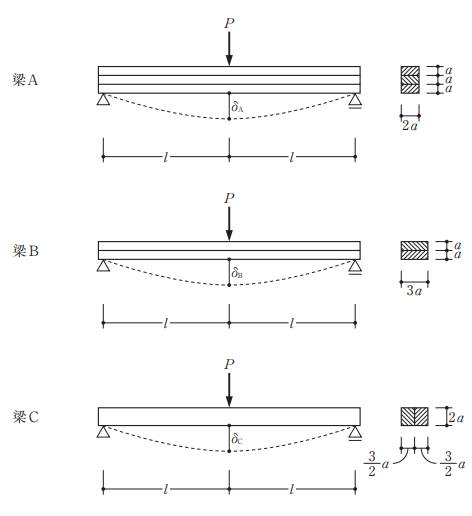
図のように、材料とスパンが同じで、断面が異なる単純梁A、B及びCの中央に集中荷重P が作用したとき、それぞれの梁の曲げによる中央たわみδA、δB及びδCの大小関係として、正しいものは、次のうちどれか。ただし、それぞれの梁は全長にわたって等質等断面の弾性部材とし、自重は無視する。また、梁を構成する部材の接触面の摩擦及び接着はないものとする。
- \(\delta_{A}\lt\delta_{B}=\delta_{C}\)
- \(\delta_{A}=\delta_{B}\lt\delta_{C}\)
- \(\delta_{B}=\delta_{C}\lt\delta_{A}\)
- \(\delta_{C}\lt\delta_{A}=\delta_{B}\)
この問題キーワードは
- 複数断面の場合の剛性の計算
- たわみの算出のしかた
前提条件
この問題はまず断面二次モーメントとたわみの算出方法について理解する必要があります。
断面二次モーメントとは
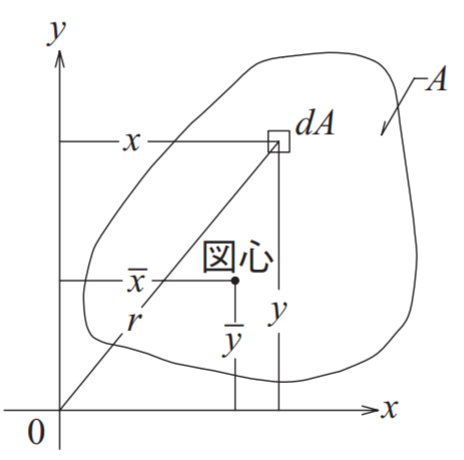
断面二次モーメントとは形による変形のしやすさを表すパラメーターです。特徴は値が大きいほど変形しにくく、小さいほど変形しやすくなります。
記号は[I]で表すことが多く、x軸周りは[Ix] y軸周りは[Iy]のように表記します。単位はおもに[cm4]や[mm4]で表すことが多いです。
断面二次モーメントの詳しい解説は以下の記事を参考にして下さい。
ヤング係数は材料そのものによって決まる値で木材なら木材、鉄なら鉄、コンクリートならコンクリートのヤング係数を使うことになります。
部材の変形しやすさは主にヤング係数と断面二次モーメントで決まり、断面二次モーメントとヤング係数を掛け合わせ、部材の曲がりにくさを表した値を曲げ剛性と呼びます。
たわみの求め方
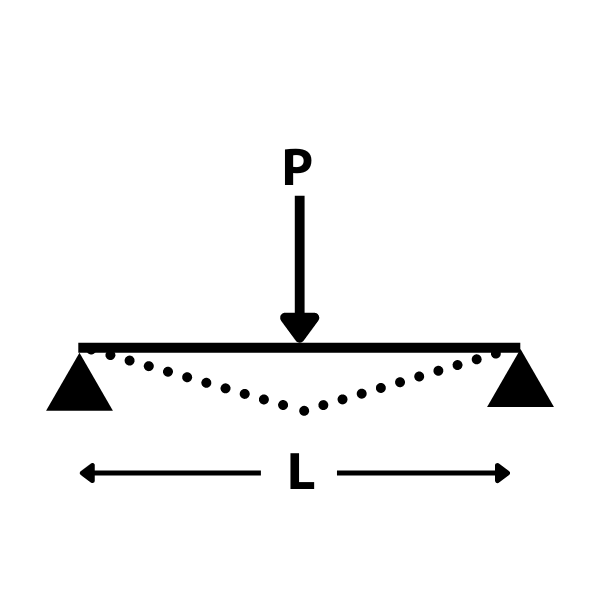
単純梁・集中荷重のたわみを式で表すと
\(\delta=\dfrac{PL^3}{48EI}\)
δ:たわみ(梁中央)
P:集中荷重
L:梁長
E:ヤング係数
I:断面二次モーメント
たわみの公式はたくさんあってややこしいです、計算でも求めることができますが覚えてしまった方が圧倒的に早いです。単純梁・集中荷重のたわみの語呂あわせは「弱った(48)エイ(EI)をプール(PL)でみた(3乗)」です。
詳しい内容はこちらの記事を参考にしてみて下さい。
解き方
今回の問題の解く順序は
- 断面二次モーメントを計算する
- スパンによるたわみの違いを計算する
ひとつずつ算出していきましょう。
まずは断面二次モーメントをそれぞれ計算していきます。今回のように断面が分割されている場合は
(分割された断面の数)×(断面二次モーメント) で計算します。
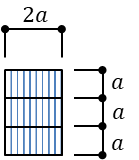
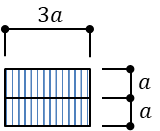
梁Aの分割した内のひとつの断面二次モーメントは
\(I_{A}’=2a*(a)^3/12=a^4/6\)
さらに分割数分を3倍にするので
\(I_{A}=a^4/2\)
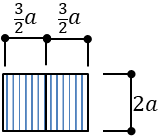
梁Bの分割した内のひとつの断面二次モーメントは
\(I_{B}’=3a*(a)^3/12=a^4/4\)
さらに分割数分を2倍にするので
\(I_{B}=a^4/2\)
梁Cの分割した内のひとつの断面二次モーメントは
\(I_{C}’=3a/2*(2a)^3/12=a^4\)
さらに分割数分を2倍にするので
\(I_{C}=2a^4\)
つぎに単純梁・集中荷重のたわみについてスパン・ヤング係数・荷重がすべて同じになるため単純にI(断面二次モーメント)の大きさが大きくなればたわみが小さくなります。
\(\delta=\dfrac{PL^3}{48EI}\)
したがって梁Cの断面二次モーメントが大きいので、たわみが小さくなり、梁Aと梁Bは断面二次モーメントが小さいのでたわみが大きくなります。
上記をまとめると答えは④となります。
まとめ
今回は2022年 一級建築士 学科試験Ⅳ構造 No.2の解説をしてきました
今回の問題のポイントは分割された断面二次モーメントの算定のしかたです。普段見慣れない計算方法で解くのが難しく感じるかもしれませんがひとつずつ紐解いていけば簡単な問題です。
ぜひ何度も読み返し解けるのようになって下さい!!
こちらは類似の問題ですので参考にしてみて下さい。
対策
- 断面が複数で矩形以外の場合
- 梁のスパンが異なる場合
こちらも自分で問題を作って解いてみるとよいでしょう!!





コメント